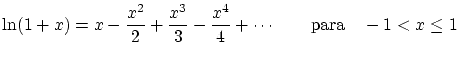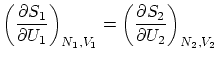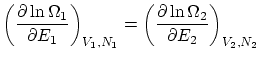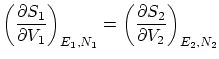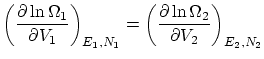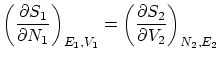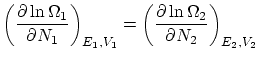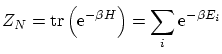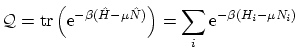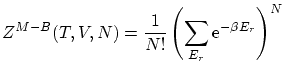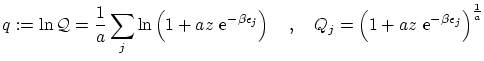Física estadística
pod
Date: Febrero-Mayo de 2002
Introducción
Los apuntes recogidos en el presente documento corresponden al temario de la asignatura de tercer curso Física Estadística de la Facultad de Física de la Universidad de Barcelona. Se tratan los temas clásicos de la física estadística, en el marco de la teoría de las colectividades de Gibbs, así como una pequeña introducción a la estadística cuántica.El enfoque elegido para el presente curso de física estadística, al contrario que otros textos más tradicionales, es el de fundamentar toda la teoría a partir de la colectividad microcanónica, deduciendo el resto de colectividades a partir de ésta. Además, se da por separado toda la teoría, dejando para un documento posterior su aplicación a sistemas físicos concretos.
1. Fundamentos de la física estadística
La física estadística se encarga de unir las teorías microscópicas (física clásica, cuántica, relatividad, electromagnetismo,...) con las teorías macroscópicas (termodinámica, medios continuos,...).
La física estadística se divide en:
- física estadística de equilibrio bien fundamentada y comúnmente aceptada y
- física estadística de no equilibrio diferentes fundamentaciones según los problemas a tratar.
Otra clasificación se refiere a si la formulación tiene en cuenta la coherencia cuántica (física estadística cuántica) o no (física estadística clásica).
Existen dos formulaciones diferentes de la física estadística:
- la teoría argódica (iniciada por Einstein) según la cual el sistema físico explora todos sus estados microscópicos posibles, mientras que el estado macroscópico viene descrito mediante promedios temporales, si bien esta teoría es de poco interés práctico para la comprensión de los sistemas físicos.
- la teoría de colectividades de Gibbs en la que se tienen una colección infinita de copias del sistema, cada una en un estado microscópico diferente.
2. La colectividad microcanónica
2.1 La teoría de colectividades
Llamaremos macroestado a cada estado posible del conjunto de variables macroscópicas (termodinámicas) con las cuales describimos el sistema. Igualmente, llamaremos microestado a todos los valores posibles de las variables microscópicas con las que describimos completamente el estado a nivel microscópico del sistema. LlamaremosEn la teoría de colectividades tenemos muchas copias del sistema, cada una en un microestado diferente, todos compatibles con el mismo macroestado del sistema. La media entre todos los sistemas nos da el estado termodinámico.
Cada tipo de sistema se adapta a un tipo de colectividad, según las restricciones que le imponemos. En este capítulo, comenzaremos por estudiar la colectividad microcanónica, adecuada para los sistemas aislados completamente del resto del universo.
2.2 Postulados de la física estadística
Presentamos a continuación los tres principales postulados de la física estadística y sus principales consecuencias.
Como consecuencia de éste postulado solamente puedo aspirar a conocer el número de microestados ![]() , pero ninguna
información adicional. Por la condición de normalización, la probabilidad de un microestado en concreto será
, pero ninguna
información adicional. Por la condición de normalización, la probabilidad de un microestado en concreto será
![]() .
.
2.3 Equilibrio termodinámico en la colectividad microcanónica
Para empezar, supondremos dos sistemas en equilibrio termodinámico entre si pero aislados del resto del universo. Fijamos la energía total a un valor
Si la los sistemas no interaccionan entre si, o lo hacen tan débilmente que podemos despreciar la contribución de la interacción,
el número de microestados factoriza
![]() .
.
Si la pared que une los dos sistemas es diaterma, rígida e impermeable (tan sólo deja pasar la energía, ![]() y
y ![]() fijos ), la termodinámica nos dice que las temperaturas de los dos subsistemas serán iguales. Esta igualdad se puede escribir, en
función de la entropía, como
fijos ), la termodinámica nos dice que las temperaturas de los dos subsistemas serán iguales. Esta igualdad se puede escribir, en
función de la entropía, como
Por otra parte, del postulado dos
![]() ha de ser máximo
respecto la energía. La condición de máximo para
ha de ser máximo
respecto la energía. La condición de máximo para ![]() nos da
nos da
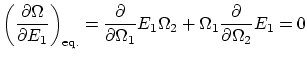
si aplicamos la regla de la derivación en cadena a la segunda derivada, y tenemos en cuenta que
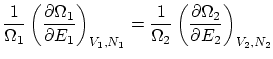
o bien
Si relajamos la condición de rigidez, la termo nos dice que, además, ha de ser ![]() . Esta igualdad se puede reescribir como
. Esta igualdad se puede reescribir como
Siguiendo el mismo procedimiento que en el caso anterior, imponiendo la condición de máximo respecto
Por último, si además permitimos el paso de partículas, la termodinámica nos impone la igualdad de potenciales químicos
![]() . De nuevo, esta condición se puede escribir como una igualdad entre derivadas
. De nuevo, esta condición se puede escribir como una igualdad entre derivadas
Además, obtenemos la condición de máximo respecto
2.4 Entropía de Boltzman
Del tercer postulado, las condición 2.1 debe ser equivalente a la 2.2, la 2.3 a la 2.4 y la 2.5 debe ser equivalente a la 2.6. En todas estas condiciones, la entropía juega el mismo papel que el logaritmo de
A partir de esta relación, podemos obtener la ecuación de estado y otros parámetros termodinámicos utilizando las igualdades que se demuestran en termodinámica. Las más útiles son
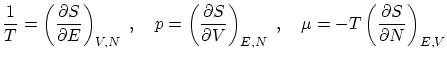
Eliminando
El hecho que la entropía ha de ser extensiva (su única dependencia con el tamaño del sistema ha de ser proporcional), nos impone la siguiente funcionalidad para el número de microestados
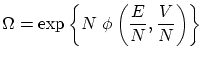
2.5 Cálculo de 
En muy pocos ejemplos prácticos podemos calcular
En el caso de microestados discretos, se recontarán los estados en una banda de energía ![]() en rededor del valor deseado.
En el limite termodinámico
en rededor del valor deseado.
En el limite termodinámico
![]() y esta aproximación no afectará a nuestro resultado.
y esta aproximación no afectará a nuestro resultado.
En el caso de microestados continuos, consideramos que el volumen de un microestado en el espacio fásico de ![]() dimensiones es
dimensiones es ![]() (hipercubo
de arista h). Dado que la fijación de la energía
(hipercubo
de arista h). Dado que la fijación de la energía
![]() nos rebaja una dimensión el espacio, debemos calcular el área de la
hipersuperficie de energía
nos rebaja una dimensión el espacio, debemos calcular el área de la
hipersuperficie de energía ![]() . Esto es equivalente a calcular el volumen entre las superficies de energías
. Esto es equivalente a calcular el volumen entre las superficies de energías ![]() y
y ![]() . Por tanto ,
. Por tanto ,
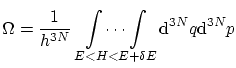
Para realizar los cálculos anteriores, puede resultar útil conocer el volumen y el área de una hiperesfera de radio ![]() :
:
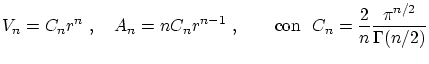
2.6 Gas ideal en la colectividad microcanónica
Supongamos un conjunto de
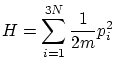
De lo dicho en el apartado anterior, debemos integrar a la superficie
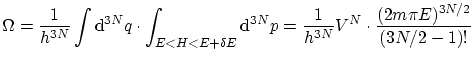
La entropía se puede calcular mediante la fórmula de Boltzman
![$\displaystyle S = k_B \ln \Omega \approx k_B N \left[ \ln V + \frac{3}{2} \ln \frac{4m \pi
E}{3h^2N}+\frac{3}{2} \right] $](img49.png)
donde hemos despreciado términos
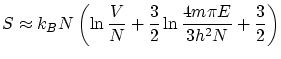
Usando las relaciones termodinámicas habituales, podemos llegar a
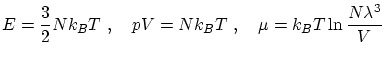
donde
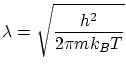
es la longitud de onda térmica de De Broglie, que se identifica con el tamaño efectivo de la partícula, es decir, la distancia a la cual dos partículas interaccionarán.
La expresión obtenida para la entropía resulta incorrecta para temperaturas muy bajas ya que
![]() , cosa prohibida
por el tercer principio de la termodinámica. La razón de este mal comportamiento reside en que para temperaturas bajas
, cosa prohibida
por el tercer principio de la termodinámica. La razón de este mal comportamiento reside en que para temperaturas bajas ![]() se hace muy grande y, por lo tanto, no podemos suponer que no existe interacción entre las partículas.
se hace muy grande y, por lo tanto, no podemos suponer que no existe interacción entre las partículas.
2.7 Gas ideal en mecánica cuántica para T altas
Vamos a considerar el mismo caso que en el apartado anterior pero introduciendo la cuantización de la energía. Veremos que llegamos al mismo valor de
En mecánica cuántica se demuestra que las energías permitidas para una partícula en una caja cúbica de arista ![]() depende de tres
números cuánticos es
depende de tres
números cuánticos es
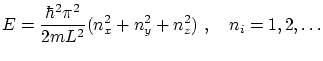
El hecho que la energía total de las
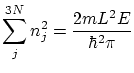
que es la ecuación de una hiperesfera en un espacio discreto de dimensión
Podemos suponer que, en este caso, el volumen de un microestado será
![]() ya que para los números cuánticos (que son naturales)
ya que para los números cuánticos (que son naturales)
![]() . Por lo tanto,
. Por lo tanto, ![]() será el volumen comprendido entre dos hiperesferas de energías
será el volumen comprendido entre dos hiperesferas de energías ![]() y
y
![]() . Dicho volumen será
igual al área de una de las hiperesferas multiplicada por
. Dicho volumen será
igual al área de una de las hiperesferas multiplicada por
![]() . Debemos tener en cuenta también que cada número
cuántico tan solo puede tomar valores positivos, por lo que debemos dividir por
. Debemos tener en cuenta también que cada número
cuántico tan solo puede tomar valores positivos, por lo que debemos dividir por ![]() . O sea
. O sea
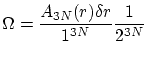
substituyendo los valores dados, encontramos la misma expresión que en el cálculo clásico, por lo que todos los resultados del apartado precedente siguen siendo válidos para el caso cuántico en altas energías.
3. La colectividad canónica
3.1 Equilibrio con un baño térmico
Aunque la colectividad microcanónica resulta útil para la fundamentación de la teoría, tiene graves inconvenientes ya que en ella se fija la energía interna mientras que experimentalmente tenemos baños a temperatura fija. Por otra parte, resulta difícil calcular el número de microestados de un sistema con interacción o donde importe la coherencia cuántica.
Para solucionar algunos de estos problemas se introduce la colectividad canónica, donde se sitúa el sistema en un baño térmico.
Por tanto, las variables a estudiar son ![]() ,
, ![]() y
y ![]() . El potencial termodinámico adecuado para estas variables es
. El potencial termodinámico adecuado para estas variables es ![]() .
.
Para deducir las ecuaciones de la colectividad canónica aplicaremos la microcanónica al sistema formado por el baño más el
sistema. La probabilidad que la energía (del sistema) sea ![]() será
será
donde
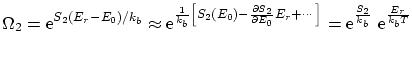
Por tanto, nos queda
donde
La función de partición canónica de esta distribución resulta ser
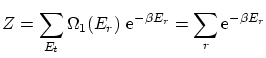
donde
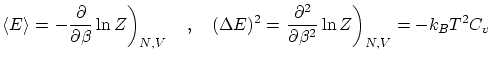
De la última relación vemos que la dispersión relativa respecto la media es muy pequeña en el límite termodinámico, por lo que la
distribución ha de ser muy picada en su máximo: el valor más probable (![]() ) es prácticamente igual al promedio. Podemos
identificar, por tanto, estos valores a la variable termodinámica
) es prácticamente igual al promedio. Podemos
identificar, por tanto, estos valores a la variable termodinámica ![]() (energía interna).
(energía interna).
3.2 La colectividad canónica y la termodinámica
Como hemos visto, la función de partición, si9 tenemos en cuenta que la distribución de la energía es muy picada entorno su valor medio, se puede escribir
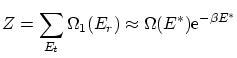
si aplicamos logaritmos obtenemos
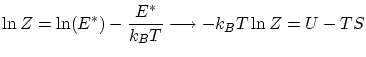
donde hemos tenido en cuenta la fórmula de Boltzmann para la entropía y que
Algunas relaciones de la termodinámica útiles en la colectividad canónica son
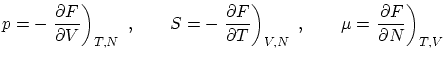
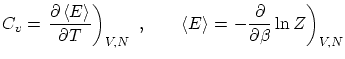
3.3 Bajas y altas temperaturas
Diremos que un sistema esta en bajas temperaturas si, para cierta temperatura y energía de referencia
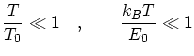
En este caso, el sistema tiende a copar los estados de energía más bajos, y, por tanto
Por el contrario, diremos que el sistema está en condiciones de temperaturas altas si
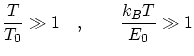
Si la energía no está acotada, pasamos al continuo (nube de probabilidad) y aplicamos el teorema de equipartición. Si la energía está acotada, tenemos
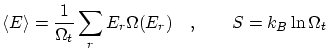
donde
3.4 Grados de libertad microscópicos
Cada variable microscópica que tenemos que especificar para describir completamente cada microestado se corresponde a un grado de libertad del sistema. Diremos que el Hamiltoniano es separable si se puede descomponer en sumandos que dependen tan sólo de las variables asociadas con un grado de libertad, i.e
En este caso, además, la función de partición factorizará y
Cada grado de libertad podrá ser discreto si
![]() en cuyo caso la función de partición se
calcula mediante el sumatorio
en cuyo caso la función de partición se
calcula mediante el sumatorio
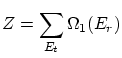
o bien continuo si
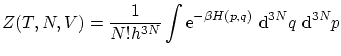
donde el factorial de
En sistemas en interacción, el hamiltoniano se puede escribir
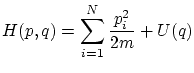
Las integrales gaussianas se pueden calcular fácilmente para llegar expresar la función de partición en términos de la integral de configuración
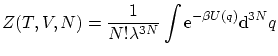
Si el sistema no esta en interacción, la función de partición factoriza de la forma
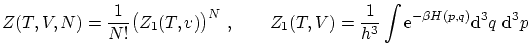
donde debemos incluir el factorial tan solo si las partículas son indistinguibles.
3.5 Teorema de equipartición de la energía
La distribución de probabilidad de Boltzmann es
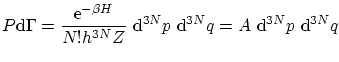
donde
Calculemos el valor esperado
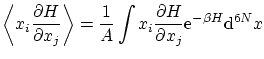
si tenemos en cuenta la igualdad
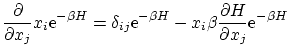
integrando por partes tenemos
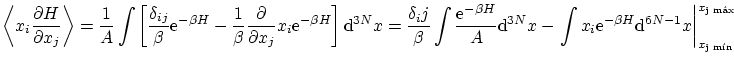
la primera integral no es mas que la condición de normalización mientras que la segunda se anula en los límites de integración de
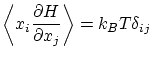
esta es la expresión (abstracta) del principio de equipartición.
Por ejemplo, si tenemos un hamiltoniano del tipo
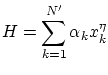
aplicando el resultado anterior para
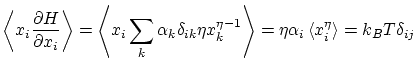
por tanto
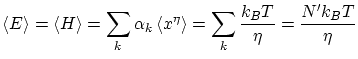
Los resultados del teorema de equipartición resultan ser completamente correctos para altas temperaturas. En capítulos posteriores re-interpretaremos este resultado a la luz de la física estadística cuántica.
4. La colectividad macrocanónica
4.1 Colectividad macrocanónica
La colectividad se introduce, principalmente, para solventar los siguientes problemas- El gran número de situaciones experimentales con interés con el número de partículas variable: reacciones químicas, equilibrio de fases, etc.
- Sistemas con gran densidad, donde la coherencia cuántica se debe tener en cuenta, son más sencillos si se deja variar el número de partículas.
Dado que en esta colectividad dejaremos sin fijar tanto la energía ![]() como el número de partículas
como el número de partículas ![]() , deberemos fijar sus
variables conjugadas: la temperatura
, deberemos fijar sus
variables conjugadas: la temperatura ![]() (conjugada a la energía) y el potencial químico
(conjugada a la energía) y el potencial químico ![]() (conjugado a
(conjugado a ![]() ).
).
Por tal de situar nuestro sistema en la fundamentación de la física estadística, enmarcada en la microcanónica (sistemas
aislados), debemos considerar el conjunto del baño térmico (que, a la vez, actuará como ``reservoir4.1'' de partículas) y el sistema que queremos estudiar. Consideraremos la energía del sistema total fijada al
valor ![]() , que el número total de partículas es
, que el número total de partículas es ![]() y que el volumen que comprende es
y que el volumen que comprende es ![]() . Llamaremos
. Llamaremos ![]() a la energía del
subsistema objeto de estudio,
a la energía del
subsistema objeto de estudio, ![]() a su número de partículas y
a su número de partículas y ![]() es su volumen. Para referirnos al baño indicaremos un
subíndice ``2''. Las propiedades del baño serán, pues
es su volumen. Para referirnos al baño indicaremos un
subíndice ``2''. Las propiedades del baño serán, pues
Excepto una constante de normalización ![]() , la probabilidad de que el sistema estudiado tenga energía
, la probabilidad de que el sistema estudiado tenga energía ![]() y
y ![]() partículas
será
partículas
será
De la microcanónica sabemos que la entropía del baño será
Si desarrollamos por Taylor tenemos
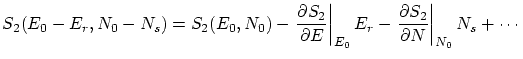
Por las relaciones termodinámicas conocidas en capítulos anteriores, podemos escribir las derivadas anteriores en función de variables termodinámicas conocidas, i.e
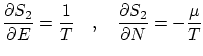
es decir, recopilando todas las relaciones
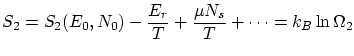
por lo que podemos escribir
donde
Podemos introducir el valor de ![]() en la expresión de la probabilidad. Como
en la expresión de la probabilidad. Como
![]() es un valor fijo, podemos absolverlo en la
constante de normalización, por lo que nos queda
es un valor fijo, podemos absolverlo en la
constante de normalización, por lo que nos queda
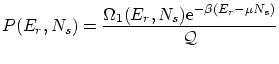
Por la condición de normalización la suma de todas las probabilidades extendida a todos los valores de la energía y del número de partículas debe ser la unidad, por lo que debe cumplirse
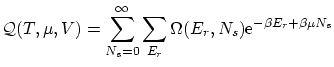
ésta es la función de partición macrocanónica.
Una variable útil para escribir la función de partición es la fugacidad
![]() . La función de
partición queda
. La función de
partición queda
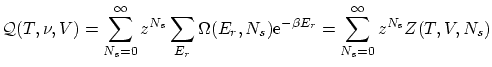
donde
4.2 Fluctuaciones y valores medios
Como es habitual en la técnica de la función de partición, se pueden escribir los valores medios y las fluctuaciones como simples derivadas. Para el número de partículas, tenemos que el valor medio se puede expresar de tres formas diferentes
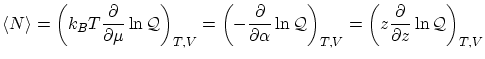
por lo que respecta a las fluctuaciones, tenemos
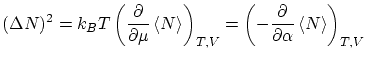
Este resultado se puede re-interpretar en términos de funciones respuesta desarrollando la derivada respecto el potencial químico en función del volumen específico
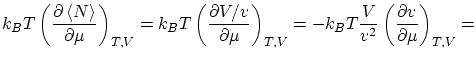 |
|||
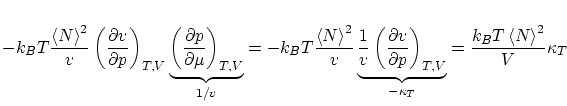 |
donde
Por cálculos similares se puede demostrar que el valor esperado de la energía es
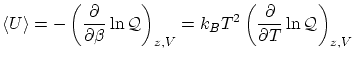
Por otra parte, las fluctuaciones son
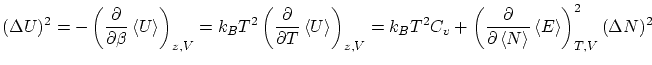
4.3 Colectividad macrocanónica y termodinámica
La termodinámica nos asegura que para una situación de equilibrio con un baño térmico y un reservoir de partículas existe un potencial privilegiado: el gran potencial
Además, se demuestra que para el sistema hidrostático se tiene
De la termodinámica sabemos, también, que la entropía se puede escribir como una simple derivada del gran potencial
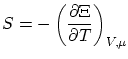
Por analogía con la colectividad canónica postulamos la relación
Naturalmente este postulado deberá contrastarse experimentalmente para ser considerado cierto.
La ecuación de estado se obtiene eliminando el potencial químico entre la definición del gran potencial y la ecuación del número
medio de partículas. El resto de magnitudes termodinámicas se obtienen a partir de la entropía ![]() , donde tenemos que
haber eliminado el potencial químico.
, donde tenemos que
haber eliminado el potencial químico.
4.4 Equivalencia entre colectividades
Tal y como hemos demostrado anteriormente, las fluctuaciones respecto de la media son muy pequeñas tanto para la energía como para el número de partículas. Por lo tanto, en el sumatorio que da lugar a la función de partición prácticamente solamente contribuirán los valores
y, por tanto, el gran potencial será
que es justamente la definición del gran potencial. Esta es una prueba más de que, en el límite termodinámico, nuestro postulado sobre el gran potencial es correcto.
4.5 Sistemas ideales
Anteriormente hemos visto que podemos escribir la función de partición grancanónica de la guisa
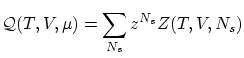
Si el sistema esta compuesto por ![]() partículas idénticas, indistinguibles, según la corrección de Gibbs se puede escribir
partículas idénticas, indistinguibles, según la corrección de Gibbs se puede escribir
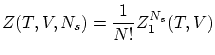
Por tanto, la función de partición macrocanónica se puede escribir
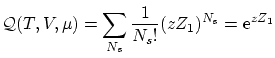
donde hemos empleado la serie de Taylor de la exponencial. Por último, en caso de partículas idénticas e indistinguibles se puede escribir el gran potencial como
Si las partículas están localizadas no procede utilizar la corrección de Gibbs i, por tanto, la función de partición resulta ser
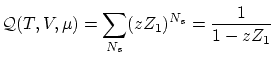
y el gran potencial queda
Dado que el logaritmo solamente está definido real para valores positivos, tenemos una cota sobre el potencial químico,
5. Estadística cuántica
5.1 Introducción
En mecánica cuántica se pueden calcular los valores esperados de un operador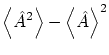 |
Una manera alternativa de realizar estos cálculos consiste en introducir una operador matriz densidad
![]() de forma que
los valores esperados se pueden escribir en forma de traza, i.e
de forma que
los valores esperados se pueden escribir en forma de traza, i.e
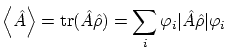
donde
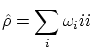
Las constantes ![]() se pueden interpretar como la probabilidad de cada estado
se pueden interpretar como la probabilidad de cada estado
![]() . La condición de normalización se puede
demostrar considerando el valor esperado del operador identidad
. La condición de normalización se puede
demostrar considerando el valor esperado del operador identidad
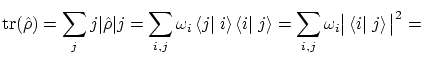 |
|||
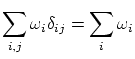 |
En equilibrio, la matriz de densidad no debe ser función, pero si debe depender de las variables del sistema. La única constante del movimiento que cumple estas condiciones es el hamiltoniano, es decir
5.2 Colectividades cuánticas
Microcanónica
En la microcanónica cuántica todos los estados deben ser equiprobables i, por tanto, todos los
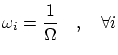
donde
Sin embargo, estos resultados no nos ayudan a imponer las condiciones de simetría i antisimetría de las funciones de onda, ya que no sabemos cual es la base adecuada del espacio de Hilbert.
Canónica
Definimos la matriz de densidad, por comparación con la probabilidad en la canónica, de la manera siguiente:
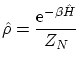
Si imponemos la condición de que la traza debe ser igual a la unidad, teniendo en cuenta que los estados propios de la matriz densidad lo son también de la energía, tenemos
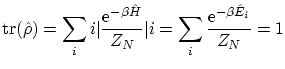
de donde
que es la misma definición de la función de partición canónica. Sin embargo, continuamos sin poder encontrar la base que implemente las condiciones de coherencia.
Macrocanónica
En este caso, tenemos dos operadores
i, por tanto, podemos encontrar una base donde los dos toman forma diagonal, i.e
La matriz densidad vendrá dada por la misma expresión que en la canónica nos da la probabilidad, es decir
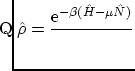
i, por tanto, la función de partición macrocanónica toma la forma ya conocida
Más adelante veremos que el hecho de tener la libertad del número de partículas nos facilita la introducción de las condiciones de coherencia.
5.3 Sistemas de partículas idénticas
5.3.1 Condiciones de coherencia
Un sistema estará compuesto de partículas idénticas si no existe ningún observable que distinga dos partículas. Esto es lo mismo que decir que el hamiltoniano
Los estados propios del hamiltoniano lo serán también del operador de permutación, es decir
Dado que
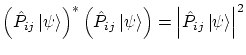 |
i, por tanto, los valores propios tendrán modulo unidad. Por ser un operador autoadjunto, tenemos
El siguiente teorema nos dice que tipo de partículas cumplen la igualdad con signo positivo y cuales con signo negativo.
- Bosones:
- Son las partículas con spin enero
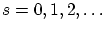 . Sus funciones de onda son simétricas, es decir,
cumplen la igualdad 5.3 con signo positivo, i.e
. Sus funciones de onda son simétricas, es decir,
cumplen la igualdad 5.3 con signo positivo, i.e
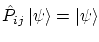
Los bosones siguen la estadística de Bose-Einstein. - Fermiones:
- Son las partículas con spin semimpar
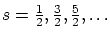 . Sus funciones de onda son
antisimétricas, es decir, cumplen la igualdad 5.3 con signo negativo, i.e
. Sus funciones de onda son
antisimétricas, es decir, cumplen la igualdad 5.3 con signo negativo, i.e
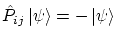
Los fermiones siguen la estadística de Fermi-Dirac.
5.3.2 Principio de exclusión de Pauli para fermiones
Denotaremos, en general, las coordenadas de cada partícula por
Si
![]() esta última igualdad implica que la función de onda debe ser nula. Dado que
esta última igualdad implica que la función de onda debe ser nula. Dado que ![]() no es una solución
físicamente aceptable debemos exigir que, para un sistema de fermiones todas las coordenadas generalizadas
no es una solución
físicamente aceptable debemos exigir que, para un sistema de fermiones todas las coordenadas generalizadas ![]() sean diferentes. Es
decir, todos los fermiones deben ocupar estados diferentes. Este es el principio de exclusión de Pauli.
sean diferentes. Es
decir, todos los fermiones deben ocupar estados diferentes. Este es el principio de exclusión de Pauli.
5.3.3 N partículas idénticas i libres
Para un sistema de
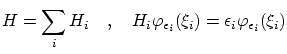
donde
Esta función es propia del hamiltoniano total, pero no implementa las condiciones de coherencia. Podemos escribir la función de onda de un sistema de N fermiones o bosones como combinación lineal de funciones de onda de este tipo.
Para los fermiones, debemos escribir la función de onda como una combinación antisimétrica de los niveles mono particulares, es decir
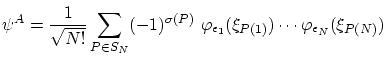
donde
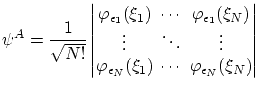
Para los bosones la función de onda simétrica, ya normalizada,resulta ser
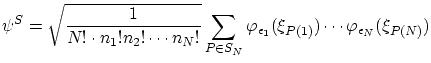
donde
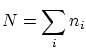
Con estas funciones de onda se pueden calcular las correspondientes funciones de partición, según la definición 5.1. Se puede demostrar que, en general, se cumplen las desigualdades
donde la función de partición en la estadística de Maxwell-Boltzman se calcula sin tener en cuenta fenómenos cuánticos, pero incluyendo el factor de Gibbs
5.4 Función de partición del sistema de N partículas
Para los sistemas de Maxwell-Boltzman podemos obtener la función de partición en la colectividad canónica según la expresión 5.4. En cambio, no es sencillo calcular la función de partición para las estadística de Bose-Einstein y de Fermi-Dirac en la colectividad canónica. Para poder proseguir, debemos pasara la colectividad macrocanónica.
Si el hamiltoniano no crea ni destruye partículas,
![]() , podemos encontrar una base
, podemos encontrar una base
![]() propia de los
operadores
propia de los
operadores ![]() y
y ![]() a la vez. Sobre esta base, el factor de la macrocanónica actuará trivialmente, i.e
a la vez. Sobre esta base, el factor de la macrocanónica actuará trivialmente, i.e
Por construcción,
![]() se construirá como producto directo de las funciones de onda monoparticulares. Por lo tanto, se
cumplirán las relaciones siguientes
se construirá como producto directo de las funciones de onda monoparticulares. Por lo tanto, se
cumplirán las relaciones siguientes
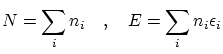
Donde
En consecuencia, la función de partición macrocanónica se puede escribir, según 5.2,
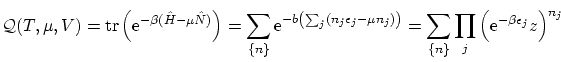
donde
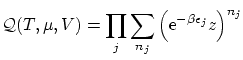
Vemos que se puede descomponer como el producto de funciones de partición

Si queremos particularizar al caso de los bosones debemos realizar el sumatorio desde ![]() hasta
hasta
![]() . La serie,
que resulta ser geométrica, puede sumarse5.1 fácilmente para obtener
. La serie,
que resulta ser geométrica, puede sumarse5.1 fácilmente para obtener
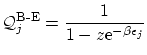
donde, para garantizar la convergencia de la serie, debemos exigir
i, en concreto, el potencial químico ha de ser menor que el más pequeño de los estados energéticos (el estado fundamental del sistema),
Por otra parte, en el caso de los fermiones, los números de ocupación, por el principio de exclusión, ![]() i, por tanto,
i, por tanto,
Por último, recordemos que para las partículas clásicas (indistinguibles), la función de partición se puede escribir de la forma
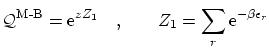
Se pueden escribir todas estas fórmulas de forma unificada de la forma siguiente
donde

Para el caso de fermiones y bosones, con estos valores de
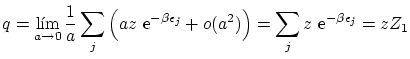
que es el resultado esperado.
5.5 Estadística de los números de ocupación
En la notación unificada 5.5 podemos calcular fácilmente el valor esperado del número de partículas
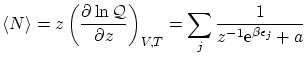
Vemos que el valor esperado del número de partículas se puede descomponer como el valor esperado de los números de ocupación
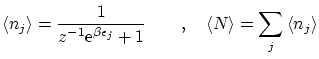
Por otra parte, podemos calcular las fluctuaciones de la forma habitual
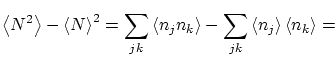 |
|||
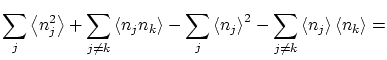 |
|||
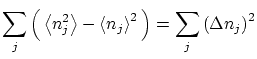 |
donde hemos usado que los
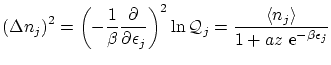
5.6 Límites de la estadística cuántica
5.6.1 Límite clásico
El límite clásico viene dado por
donde las tres estadísticas coinciden. Esta condición es equivalente a imponer
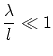
en donde
En la demostración rigurosa del límite clásico aparece, de forma natural, el factorial de Gibbs y el factor ![]() , hecho que
justifica las hipótesis realizadas en capítulos precedentes.
, hecho que
justifica las hipótesis realizadas en capítulos precedentes.
5.6.2 Límite continuo
En el límite continuo podemos substituir los sumatorios por integrales
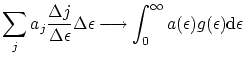
La función
De esta forma, podemos escribir la función de partición
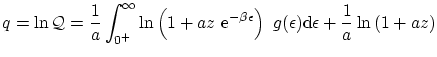
donde hemos incluido el primer termino del sumatorio (el nivel fundamental) para tenerlo en cuenta en los cálculos en aquellas situaciones en que
De idéntica forma, podemos escribir el número medio de partículas
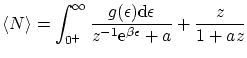
i la energía
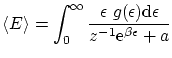
donde hemos eliminado el término referente al estado fundamental ya que no aporta energía.
Por último, podemos escribir las fluctuaciones
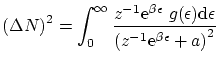
Footnotes
- ... ``reservoir4.1
- Diremos que un sistema es un ``reservoir'' de partículas si es capaz de intercambiar tantas partículas con cualquier otro subsistema sin variar su potencial químico.
- ... sumarse5.1
- La suma de la serie geométrica es muy sencilla, para
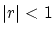 tenemos
tenemos 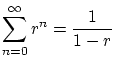
- ... logaritmo5.2
- El desarrollo Taylor del logaritmo neperiano es