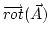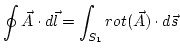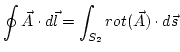Secciones Destacados Apuntes

Página principal Apuntes Mecánica (I) Tratamiento y propagación de errores Gravitación newtoniana Física general de fluidos Fundamentos de astronomía Termodinámica Relatividad especial Física cuántica Física estadística Teoría elemental de campos Teoría de la probabilidad Transformadas integrales Teoría de Strum-Liouville Generación de números aleatorios Making TeX Work FAQ española FAQ inlesa Microscopía de transmisión de electrones Secciones ¿Qué es la Física? Foros Blogs de Física Colección de problemas Libros Diccionarios Desafío y concursos Por rama Mecánica clásica Electromagnetismo Termodinámica y estadística Relatividad Cuántica Métodos matemáticos Astronomía Fluidos y medios contínuos Óptica Física de partículas Física del estádo sólido Física avanzada Física cotidiana Historia de la Física Por nivel Divulgación Iniciación Secundaria Primer ciclo Segundo ciclo Avanzado Por tipo Apuntes Chuletarios Artículos Trabajos Libros digitales Prácticas de laboratorio Software Otros Editorial URSS LaTeX Preguntas más frecuentes Humor Software para la física Enlaces Acerca de ...

Búsqueda

¡Bájatelo!

¡Coméntalo en el foro!

Teoría elemental de campos

Barbol

Curso 2001

Introducción

Estos apuntes corresponden al tema 3 Teoría elemental de campos impartido en el curso de Física Xeral del año 2001 en la Facultade de Físicas da Universidade de Santiago de Compostela por el profesor Lisardo Núñez. Se omiten las demostraciones de los teoremas de Ostrogradski-Gauss y Stokes, que se pueden encontrar en bastantes libros que tratan las integrales curvilíneas y de superficie en alguno de sus temas (algunos ejemplos son Cálculo vectorial de Mardsen y Tromba, Cálculo diferencial e integral de N. Piskunov o Campos electromagnéticos de R. K. Wangsness).

1 Campos escalares y vectoriales

Se dice que en una región del espacio existe un campo cuando a cada punto de esa región se le puede asignar un valor único de determinada magnitud.

En el caso de que la magnitud sea un escalar se dirá que el campo es escalar. Por el contrario, si la magnitud es de carácter vectorial diremos que se trata de un campo vectorial.

1.1 Campo escalar

Analíticamente un campo escalar es una función $U:\mathbb{R}^{n}\rightarrow\mathbb{R}$ que asigna a cada valor de $\vec{r}$ un único valor $U(\vec{r})$.

Geométricamente un campo escalar se representa mediante las superficies isoescalares (superficies en las que el el valor $U(\vec{r})$ se mantiene constante). Dependiendo de la magnitud de la que se trate las superficies isoescalares tomarán un nombre u otro (isotermas, isobaras, etc.).

Debido a la definición de campo escalar dos superficies isoescalares nunca pueden cortarse.

1.2 Campo vectorial

Analíticamente un campo vectorial es una función $\vec{A}:\mathbb{R}^{n}\rightarrow\mathbb{R}^{n}$ que asigna a cada valor de $\vec{r}$ un único valor $\vec{A}(\vec{r})$.

La representación geométrica de los campos vectoriales se realiza mediante las líneas vectoriales, de modo que el campo es tangente a la línea vectorial en todos sus puntos. De modo que si el elemento diferencial de la línea vectorial es $d\vec{l}$ tenemos siempre que $\vec{A}$ es paralelo a $d\vec{l}$.

Debido a la definición de campo vectorial dos líneas vectoriales nunca pueden cortarse.

1.2.1 Teorema de Helmholtz

El teorema de Helmholtz nos garantiza que para especificar de modo unívoco un campo vectorial basta con conocer su divergencia (véase la sección 8) y su rotacional (véase la sección 9) en todos los puntos de una región finita.

Dado que el campo vectorial puede encontrarse a partir de ellas, la divergencia y el rotacional reciben el nombre de fuentes del campo. El punto en el que se calcula el valor del campo vectorial recibe el nombre de punto campo.

Si existen fuentes en el infinito (no todas están restringidas a un volumen finito) este teorema no es absolutamente cierto, ya que se deben incluir ciertas integrales de superficie que involucran al propio campo.

2 Derivada direccional

Supongamos que existe un campo escalar $U=U(\vec{r})$ en una región del espacio y que tomamos dos superficies isoescalares $U_{1}$ y $U_{2}$ infinitamente próximas. Supongamos que tenemos el punto $P$ en $U_{1}$ y el punto $Q$ en $U_{2}$ unidos mediante el vector $d\vec{r}$.

Tras estas suposiciones podemos afirmar que la variación que experimenta el campo escalar entre $P$ y $Q$ es $U_{2}-U_{1}=dU$ (ya que están infinitamente próximas). La variación de $U$ en derivadas parciales es:

$$dU=\frac{\partial U}{\partial x}dx+\frac{\partial U}{\partial y}dy+\frac{\partial U}{\partial z}dz$$ (1)

Definimos el gradiente de la función escalar $U$ como $grad(U)=\frac{\partial U}{\partial x}\hat{\imath}+\frac{\partial U}{\partial y}\hat{\jmath}+\frac{\partial U}{\partial z}\hat{k}$¹, en donde $\hat{\imath}$, $\hat{\jmath}$ y $\hat{k}$ son los versores o vectores directores de las coordenadas cartesianas $x$, $y$ y $z$ respectivamente. Por tanto tenemos que

$$dU=grad(U)\cdot d\vec{r}$$ (2)

Hay que hacer notar que en la ecuación (1) se emplean las coordenadas cartesianas mientras que en la ecuación (2) no se especifica ningún tipo de coordenadas.

Por tanto tenemos

$$dU=grad(U)\cdot d\vec{r}=grad(U)\cdot\frac{\vec{r}}{\vert\vec{r}\vert} dr \Rightarrow \frac{dU}{dr}=grad(U)\hat{r}$$ (3)

en donde $\frac{\vec{r}}{\vert\vec{r}\vert}=\hat{r}$ es un vector de módulo unidad y dirección la del vector $\vec{r}$ y $\frac{dU}{dr}$ es la derivada direccional: la variación de $U$ por unidad de $r$ cuando nos desplazamos en la dirección de $\vec{r}$).

3 El operador nabla

Se define al operador nabla (generalmente representado como $\nabla$ o $\vec{\nabla}$) como un operador diferencial de carácter vectorial, de modo que

$$\nabla=\frac{\partial}{\partial x}\hat{\imath}+\frac{\partial}{\partial y}\hat{\jmath}+\frac{\partial}{\partial z}\hat{k}$$ (4)

A veces también se le llama operador de Hamilton o hamiltoniano.

Hay que notar que esta definición del operador nabla está dada en coordenadas cartesianas, y que la forma del operador cambiará si la aplicamos a un sistema que use coordenadas de cualquier otro tipo. La forma de este operador en coordenadas cilíndricas sería

$$\nabla=\frac{\partial}{\partial\rho}\hat{\rho}+\frac{1}{\rho... ...artial\varphi}\hat{\varphi}+\frac{\partial}{\partial z}\hat{z}$$ (5)

y en coordenadas esféricas

$$\nabla=\frac{\partial}{\partial r}\hat{r}+\frac{1}{r}\frac{\... ...c{1}{r sen\theta}\frac{\partial}{\partial\varphi}\hat{\varphi}$$ (6)

4 Gradiente de un campo escalar

Se define el gradiente de una función (generalmente una función de tres variables) como

$$grad(U)=\nabla U$$ (7)

Supongamos una superficie isoescalar, en este caso el cambio en la magnitud $U$ es nulo, por tanto tenemos

$$dU=0=\nabla U\cdot d\vec{r}\Rightarrow\nabla U\perp d\vec{r}$$ (8)

El gradiente de $U$ debe ser perpendicular en cada punto a la superficie isoescalar a la que pertenece el punto. Por convenio el sentido del gradiente de $U$ es hacia valores creciente de $U$, es decir

$$\nabla U=\left(\frac{dU}{dr}\right)_{max}$$ (9)

5 Circulación de un campo vectorial

Supongamos que tenemos una región del espacio en la que existe un campo vectorial $\vec{A}=\vec{A}(x,y,z)$, y que tenemos una línea (de forma arbitraria) acotada entre dos puntos $M$ y $N$. En este caso definimos la circulación elemental del campo $\vec{A}$ como:

$$dC=\vec{A}\cdot d\vec{l}=A_{x}d{x}+A_{y}d{y}+A_{z}d{z}$$ (10)

Por lo tanto la circulación del campo $\vec{A}$ es una integral de línea de la forma $C=\int_{M}^{N}\vec{A}\cdot d\vec{l}=\int_{M}^{N}(A_{x}d{x}+A_{y}d{y}+A_{z}d{z})$, que a priori no tiene por qué ser fácil de calcular. Supongamos ahora que el campo vectorial $\vec{A}$ es el gradiente de un campo escalar $U$, es decir: $\vec{A}=grad(U)$, en ese caso:

$$C=\int_{M}^{N}\vec{A}\cdot d\vec{l}=\int_{M}^{N}grad(U)\cdot d\vec{l}=\int_{M}^{N}dU=U(N)-U(M)$$ (11)

De modo que en el caso de que el campo vectorial sea el gradiente de un campo escalar, la circulación de éste es independiente del camino, sólo depende del valor que toma el campo escalar en los extremos. En este caso diremos que hablamos de un campo conservativo. $U$ se denomina función potencial (es decir, una función genérica de la que se deriva un campo conservativo). El valor que $U$ toma en cada punto se denomina potencial.

Además se puede ver que lo recíproco también es cierto: todo campo cuya circulación sólo dependa del valor inicial y final de la integral es un campo de gradientes.

Por tanto, en un campo conservativo la integral de circulación a lo largo de una línea cerrada (es decir, el punto inicial y el final son el mismo) es cero. Sin embargo lo recíproco no es cierto.

6 Representación vectorial de superficies

Una superficie siempre se puede representar por un vector con módulo igual al área de la superficie, dirección perpendicular a la superficie en cada punto y sentido elegido por convenio.

Si la superficie es una superficie abierta se suele escoger el que convenga para cada problema. Si la superficie es cerrada el vector de superficie va dirigido siempre hacia fuera del volumen.

7 Flujo de un campo vectorial a través de una superficie

Supongamos que existe un campo vectorial $\vec{A}=A_{x}\hat{\imath}+A_{y}\hat{\jmath}+A_{z}\hat{k}$. Definimos el flujo elemental como

$$d\phi=\vec{A}\cdot d\vec{s}$$ (12)

Por tanto tenemos que $d\phi=A_{x}ds_{x}+A_{y}ds_{y}+A_{z}ds_{z}$, de modo que el flujo total es

$$\phi=\int_{\epsilon}\vec{A}\cdot d\vec{s}$$ (13)

Siendo esta una integral de superficie a realizar sobre elementos en $\epsilon$. El flujo es el número de líneas vectoriales que atraviesan la superficie. En superficies abiertas no importa si el flujo es positivo o negativo.

8 Divergencia de un campo vectorial (Teorema de Ostrogradski-Gauss)

Definimos la divergencia² de un campo vectorial $\vec{A}=A_{x}\hat{\imath}+A_{y}\hat{\jmath}+A_{z}\hat{k}$ como

$$div(\vec{A})=\frac{\partial A_{x}}{\partial x}+\frac{\partia... ...artial y}+\frac{\partial A_{z}}{\partial z}=\nabla\cdot\vec{A}$$ (14)

El teorema de Ostrogradski-Gauss nos dice que la integral de la divergencia de un campo vectorial $\vec{A}$ en un volumen es igual al flujo del campo $\vec{A}$ a través de la superficie que limita ese volumen, es decir

$$\int\!\!\!\int\!\!\!\int_{V}(\nabla\cdot\vec{A})\, d\tau=\int\!\!\!\int_{\sigma}\vec{A}\cdot d\vec{s}$$ (15)

8.1 Conclusiones del teorema de Ostrogradski-Gauss

A partir de la definición de flujo y del teorema de Gauss podemos obtener fácilmente que $\phi=\int_{\tau}{(\nabla \cdot \vec{A})\, d\tau}$, podemos hacer un cuadro para los diferentes valores posibles de $\phi$ y $\nabla\cdot\vec{A}$ y sacar algunas conclusiones:

$\phi>0\Rightarrow \int_{\tau}(\nabla\cdot\vec{A})\,d\tau>0$	$\nabla\cdot\vec{A}>0\Rightarrow\int_{\tau}{(\nabla \cdot \vec{A})\, d\tau}>0 \Rightarrow\phi>0$
$\phi<0\Rightarrow \int_{\tau}(\nabla\cdot\vec{A})\,d\tau<0$	$\nabla\cdot\vec{A}<0\Rightarrow\int_{\tau}{(\nabla \cdot \vec{A})\, d\tau}<0 \Rightarrow\phi<0$
$\phi=0\Rightarrow \int_{\tau}(\nabla\cdot\vec{A})\,d\tau=0$	$\nabla\cdot\vec{A}=0\Rightarrow\int_{\tau}{(\nabla \cdot \vec{A})\, d\tau}=0 \Rightarrow\phi=0$

De la parte izquierda de la tabla no podemos sacar conclusiones, sólo podemos decir como se comporta la región en conjunto, no como es en todos sus puntos. De la segunda parte sacamos conclusiones: al conocer su divergencia (descripción de la región) sabemos cómo es el flujo.

Cuando $\nabla \cdot \vec{A}>0$ se dice que la región es un manantial; si $\nabla \cdot \vec{A}<0$ se dice que es un sumidero y si $\nabla \cdot \vec{A}=0$ se denomina solenoidal.

9 Rotacional de un campo vectorial (Teorema de Stokes)

Definimos el rotacional³ de un campo vectorial $\vec{A}=A_{x}\hat{\imath}+A_{y}\hat{\jmath}+A_{z}\hat{k}$ como

$$rot(\vec{A})=\left(\frac{\partial A_{z}}{\partial y}-\frac{\... ...{\partial A_{x}}{\partial y}\right)\hat{k}=\nabla\times\vec{A}$$ (16)

El teorema de Stokes nos dice que la circulación de un campo vectorial $\vec{A}$ a lo largo de una línea cerrada que limita una superficie es igual al flujo del rotacional del campo vectorial a través de esa superficie, es decir

$$\int_{\lambda}\vec{A}\cdot d\vec{l}=\int\!\!\!\int_{\sigma}(\nabla\times\vec{A})\cdot d\vec{s}$$ (17)

9.1 Aplicación del teorema de Stokes

Consideremos una superficie cerrada, si la `partimos' a la mitad tenemos dos superficies ($S_{1}$ y $S_{2}$) abiertas con una línea en común. Escogemos los vectores de superficie de modo tal que la circulación sobre la línea común tenga el mismo sentido, de este modo uno de los vectores superficie tiene la dirección `saliente´ de la superficie original y el otro tiene la dirección `entrante'. En este caso tenemos, según Stokes:

$$\oint\vec{A}\cdot d\vec{l}=\int_{S_{1}}rot(\vec{A})\cdot d\vec{s} \oint\vec{A}\cdot d\vec{l}=\int_{S_{2}}rot(\vec{A})\cdot d\vec{s}$$ (18)

Por tanto tenemos que $\int_{S_{1}}rot(\vec{A})\cdot d\vec{s}=\int_{S_{2}}rot(\vec{A})\cdot d\vec{s}$.

Si ahora tomamos la suma de las dos superficies (las volvemos a juntar) obtenemos una superficie cerrada, por lo que podemos aplicar el teorema de Ostrogradski-Gauss (8).

$$\oint_{S}rot(\vec{A})\cdot d\vec{s}=\int_{\tau}div(rot(\vec{A}))\, d\tau$$ (19)

Pero además tenemos que

$$\oint_{S}rot(\vec{A})\cdot d\vec{s}=\int_{S_{1}}rot(\vec{A})\cdot d\vec{s}+\int_{S_{2}}rot(\vec{A})\cdot d\vec{s}=0$$ (20)

debido a que al ser una superficie cerrada hay que cambiar el sentido del vector superficie de una de las integrales, de modo que cambia también de signo. Igualando estas dos ecuaciones obtenemos la expresión

$$\oint rot(\vec{A})\cdot d\vec{s}=\int_{\tau}div(rot(\vec{A}))\, d\tau=0$$ (21)

Que se expresa diciendo que el flujo del rotacional de un campo de vectores a través de una superficie cerrada es emphsiempre nulo.

Para que $\int_{\tau}div(rot(\vec{A}))\, d\tau=0$ sus sumandos han de anularse o ser todos cero, en este caso tenemos que $div(rot(\vec{A}))=0$, por lo que el campo de rotacionales es siempre solenoidal.

Supongamos que tenemos ahora un campo vectorial $\vec{B}$ tal que $div(\vec{B})=0$, entonces podemos suponer que $\vec{B}=rot(\vec{A})$. El campo solenoidal $\vec{B}$ deriva del campo vectorial $\vec{A}$ al que se le llama potencial vector.

Notas al pie

...(gradiente)¹

Nótese que es un vector, algunas veces el gradiente se nota como $\overrightarrow{grad}(U)$

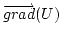
... divergencia²

Nótese que la divergencia es un escalar, ya que es el `producto escalar' de nabla por un campo vectorial

... rotacional³

Nótese que el rotacional es un vector, a veces se representa como $\overrightarrow{rot}(\vec{A})$

Acceso rápido

Secciones Destacados Apuntes

 

© 2003—2024, La web de Física
Dirección de contacto
Créditos