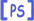Transformadas integrales
pod
Date: Marzo - abril de 2001
Introducción
Este documento presenta brevemente los principios de la teoría de las transformadas integrales, en especial, de la transformada de Laplace y la de Fourier. La transformación de Laplace es de amplia aplicación en el campo de la electrónica y l teoría de circuitos. Por otra parte, la transformada de Fourier, es de amplia aplicación en el análisis de señales, así como en diferentes campos de la física (teoría de la difracción, mecánica cuántica, etc.). Las transformadas integrales se presentan en forma de apuntes esquemáticos y sin demostraciones.
1 Transformadas integrales
![$\displaystyle \bar{F}(s) = \mathcal{I} \big[ f(x) \big] = \int_a^b\!\!f(x) K(s, x) \ensuremath{\mathrm{d}x} . $](img5.png)
Donde
El operador de transformación
![]() es lineal, así como el operación de transformación inversa
es lineal, así como el operación de transformación inversa
![]() .
.
2 Transformada de Laplace
2.1 Definición
![$\displaystyle F(s) = \ensuremath{ \mathcal{L} \left[ f(t) \right] }= \int_0^\infty \!\!f(t) e^{-st} \ensuremath{\mathrm{d}x} . $](img9.png)
Algunos ejemplos son:
![$\displaystyle \ensuremath{ \mathcal{L} \left[ e^{at} \right] }= \frac{1}{s-a} ...
...remath{ \mathcal{L} \left[ \mathbf{J}_0(t) \right] }= \frac{1}{\sqrt{1+s}} , $](img10.png)
2.2 Teoremas fundamentales
Los siguientes teoremas serán útiles para resolver ecuaciones diferenciales así como hallar transformadas inversas.
![$\displaystyle \ensuremath{ \mathcal{L} \left[ f(ct) \right] }= \frac{1}{c} F \left( \frac{s}{c} \right) . $](img27.png)
![$\displaystyle \ensuremath{ \mathcal{L} \left[ t^n f(t) \right] }= (-1)^n \frac{\ensuremath{\mathrm{d}}^n}{\ensuremath{\mathrm{d}s}^n}F(s) . $](img29.png)
2.3 Teoremas de integración y derivación
En utilizar la transformada de Laplace en ecuaciones diferenciales, las condiciones iniciales aparecen en transformar las derivadas de la función incógnita. Para obtener la ecuación general se asigna un valor constante a las condiciones iniciales. Este método suele ser útil tan solo si los coeficientes de la ecuación diferencial son polinomios de orden menor que el grado de la ecuación.
![$\displaystyle \ensuremath{ \mathcal{L} \left[ \frac{\ensuremath{\mathrm{d}f(t)}...
...rm{d}x}} \right] }= s \ensuremath{ \mathcal{L} \left[ f(t) \right] }- f(0) . $](img31.png)
En general, para ![]() , se tiene
, se tiene
![$\displaystyle \ensuremath{ \mathcal{L}_{t} \left[ \frac{\partial u(x,t)}{\parti...
... \right] }= s \ensuremath{ \mathcal{L}_{t} \left[ u(x,t) \right] }- u(x,0) , $](img37.png)
![$\displaystyle \ensuremath{ \mathcal{L}_{t} \left[ \frac{\partial u(x,t)}{\parti...
...{\partial}{\partial x} \ensuremath{ \mathcal{L}_{t} \left[ u(x,t) \right] } . $](img38.png)
En general,
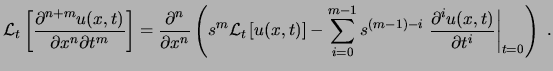
![$\displaystyle \ensuremath{ \mathcal{L} \left[ \int_0^t\!\!f(\tau) \ensuremath{\...
...}\tau} \right] }= \frac{\ensuremath{ \mathcal{L} \left[ f(t) \right] }}{s} . $](img41.png)
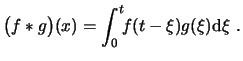
Este producto es asociativo, distributivo respecto la suma y conmutativo.
![$\displaystyle \ensuremath{ \mathcal{L} \left[ \big(f*g\big) \right] }=\ensurema...
...nt_0^t\!\! f(t-\xi) g(\xi) \ensuremath{\mathrm{d}\xi} \right] }= F(s) G(s) . $](img46.png)
2.4 Transformada de Laplace inversa
Existen diversos métodos para hallar la transformada inversa de una función:
- Descomposición en fracciones simples: Aplicable a funciones racionales polinómicas. Se descompone la función en fracciones simples, cuya transformada inversa es conocida (exponenciales, funciones trigonométricas, etc.).
- Teorema de convolución: Aplicable cuando la función es producto de dos transformadas:
![$\displaystyle \ensuremath{ \mathcal{L}^{-1} \left[ F(s) G(s) \right] }= \int^t_0\!\!f(t-\xi) g(\xi) \ensuremath{\mathrm{d}\xi} . $](img50.png)
- Segundo teorema de traslación: Si
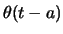 es la función escalón, tenemos
es la función escalón, tenemos
![$\displaystyle \ensuremath{ \mathcal{L}^{-1} \left[ e^{-as} F(s) \right] }= \theta(t-a) f(t-a) . $](img51.png)
![$\displaystyle \ensuremath{ \mathcal{L}^{-1} \left[ F(s) \right] }= \frac{1}{2\p...
...x s} \ensuremath{ \mathcal{L} \left[ f(x) \right] }\ensuremath{\mathrm{d}s} . $](img52.png)
3 Transformada de Fourier
3.1 Integral de Fourier
Extendiendo las series de Fourier a intervalos infinitos se puede deducir el siguiente
![$\displaystyle \frac{1}{2} \Big[ f(x^+) + f(x^-) \Big] = \frac{1}{\pi} \int_0^\i...
...os\alpha (t-x) \ensuremath{\mathrm{d}t}\right]\ensuremath{\mathrm{d}\alpha} . $](img53.png)
Para funciones pares, se tiene
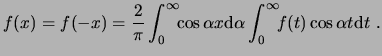
Para funciones impares, se tiene
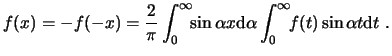
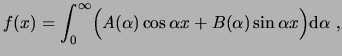
donde
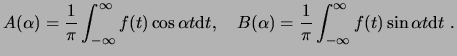
Otra manera más útil de escribir el teorema Integral de Fourier es:
![$\displaystyle f(x) = \frac{1}{2\pi}\int_{-\infty}^\infty\!\!\left[\int_{-\infty...
...ensuremath{\mathrm{d}t} \right] e^{-i\alpha x}\ensuremath{\mathrm{d}\alpha} . $](img58.png)
3.2 Transformada de Fourier
A partir del teorema integral de Fourier, se puede definir la transformada de Fourier:
![$\displaystyle \ensuremath{ \mathcal{F} \left[ f(x) \right] }\equiv F(\alpha) \e...
...t{2\pi}}\int^\infty_{-\infty}\!\!f(t) e^{i\alpha t}\ensuremath{\mathrm{d}t} , $](img60.png)
entonces,
![$\displaystyle \ensuremath{ \mathcal{F}^{-1} \left[ F(\alpha) \right] }= f(x) = ...
...nt^\infty_{-\infty}\!\!F(\alpha)e^{-i\alpha x}\ensuremath{\mathrm{d}\alpha} . $](img62.png)
De igual manera, podemos definir
![$\displaystyle \ensuremath{\mathcal{F}_{S}\left[f(x)\right]}\equiv F_S(\alpha) \...
...{1}{\sqrt{2\pi}}\int^\infty_{0}\!\!f(t)\sin\alpha t\ensuremath{\mathrm{d}t} , $](img64.png)
entonces,
![$\displaystyle \ensuremath{\mathcal{F}^{-1}_{S}\left[F(\alpha)\right]}= f(x) = \...
...{\pi}}\int_0^\infty\!\!F_S(\alpha)\sin\alpha t\ensuremath{\mathrm{d}\alpha} . $](img65.png)
![$\displaystyle \ensuremath{\mathcal{F}_{C}\left[f(x)\right]}\equiv F_C(\alpha) \...
...{1}{\sqrt{2\pi}}\int^\infty_{0}\!\!f(t)\cos\alpha t\ensuremath{\mathrm{d}t} , $](img66.png)
entonces,
![$\displaystyle \ensuremath{\mathcal{F}^{-1}_{C}\left[F(\alpha)\right]}= f(x) = \...
...{\pi}}\int_0^\infty\!\!F_C(\alpha)\cos\alpha t\ensuremath{\mathrm{d}\alpha} . $](img67.png)
3.3 Propiedades de la transformada de Fourier
Los siguientes teoremas, expresan las propiedades más útiles de la transformada de Fourier.
![$\displaystyle \ensuremath{ \mathcal{F} \left[ f(ct) \right] }= \frac{1}{\vert c\vert} F(\frac{\alpha}{c}) . $](img73.png)
En general, si las derivadas sucesivas cumplen las condiciones, tenemos
Si
![]() es una función de varias variables, entonces podemos generalizar el resultado anterior:
es una función de varias variables, entonces podemos generalizar el resultado anterior:
![$\displaystyle \ensuremath{ \mathcal{F} \left[ \frac{\partial^{n+m} u(x,y)}{\par...
...ac{\partial^m}{\partial x^m}
\ensuremath{ \mathcal{F} \left[ f(x) \right] } . $](img80.png)
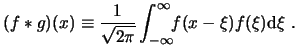
O lo que es lo mismo
![$\displaystyle \ensuremath{ \mathcal{F}^{-1} \left[ F(\alpha) G(\alpha) \right] ...
...rt{2\pi}}\int^\infty_{-\infty}\!\!f(x-\xi) f(\xi)\ensuremath{\mathrm{d}\xi} . $](img84.png)
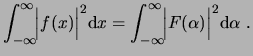
3.4 Transformada de Fourier de las funciones escalón, impulso y delta de Dirac
A partir de la semejanza entre la definición de la función delta de Dirac
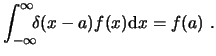
y el teorema integral de Fourier podemos encontrar una representación para la delta de Dirac:
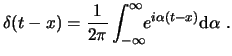
Otra representación posible es el límite de una sucesión de campanas gaussianas
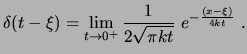
Otra representación de la delta es el límite la función impulso
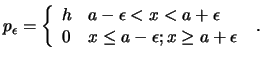
la transformada de Fourier de esta función se puede calcular
![$\displaystyle \ensuremath{ \mathcal{F} \left[ p_\epsilon(x) \right] }= \frac{2 ...
...on}{\sqrt{2\pi}} e^{i\alpha a} \frac{\sin \alpha\epsilon}{\alpha\epsilon} , $](img91.png)
tomando
Así, pues, podemos definir la transformada de Fourier de la función de Dirac se puede definir mediante el límite de dicha función:
![$\displaystyle \ensuremath{ \mathcal{F} \left[ \delta(x-a) \right] }= \lim_{\eps...
...cal{F} \left[ p_\epsilon(x) \right] }= \frac{1}{\sqrt{2\pi}} e^{ia\alpha} . $](img94.png)
Por otra parte, en aplicar la definición habitual de la transformada de Fourier a la función escalón
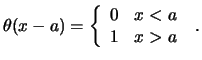
se encuentra que el resultado no existe, pero se puede definir a partir del límite
![$\displaystyle \ensuremath{ \mathcal{F} \left[ \theta(x-a) \right] }= \lim_{\bet...
...ta(x-a) e^{-\beta x} \right] }= \frac{i e^{i\alpha a}}{\sqrt{2\pi} \alpha} . $](img96.png)
3.5 Diferenciación de las transformadas de seno y coseno
Para las transformadas de Fourier existen teoremas de diferenciación análogos a los generales.
![$\displaystyle \ensuremath{\mathcal{F}_{c}\left[f''(x)\right]}= -\alpha^2 F_C(\alpha) - \sqrt{\frac{2}{\pi}} f'(0) . $](img98.png)
![$\displaystyle \ensuremath{\mathcal{F}_{s}\left[f''(x)\right]}= \sqrt{\frac{2}{\pi}} f(0) - \alpha^2 F_S(\alpha) . $](img99.png)