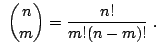Resolución de la sucesión de Fibonacci mediante los métodos matemáticos de la mecánica cuántica
pod
Date: 16 de agosto de 2003
Resumen:
Para acabar, utilizaremos la solución encontrada para demostrar explícitamente algunas de las propiedades más conocidas de la sucesión de Fibonacci, en espacial su relación existente con la razón áurea.
Las técnicas utilizadas en este artículo no precisan de conocimientos reales sobre los detalles matemáticos o fenomenológicos de la mecánica cuántica, ya que las técnicas utilizadas en ésta que se utilizan en el presente artículo son más generales y se estudian en los primeros cursos de las diferentes licenciaturas con contenido matemático medio.
Por este motivo, el presente artículo debería poder ser seguido por cualquier estudiante de primer curso de las licenciaturas de física y de matemáticas, o de segundo ciclo de carreras técnicas, sin gran dificultad. Las técnicas matemáticas utilizadas en la segunda mitad del artículo son muy frecuentes y útiles en estas carreras, por lo que la lectura detallada puede resultar instructiva.
Incluso los estudiantes de bachiller deberían comprender gran parte del documento, dejando a parte detalles matemáticos algo más adelantados.
1 Introducción
Una sucesión es una aplicación entre el conjunto de los números naturales,La forma más simple de caracterizar una sucesión de números es enumerar uno a uno todos sus elementos, por ejemplo en forma de tabla, sin embargo este procedimiento es inviable ya que nos haría falta especificar enteramente infinitos números. La formas más usuales consisten en proporcionar una regla que nos permita calcular cada nuevo término.
El método más completo consiste en dar el término general, es decir, proporcionar una fórmula matemática que nos permita obtener el valor del término n-ésimo sin necesidad de conocer ninguna información más. Un ejemplo de ésto es la sucesión de los números pares,
![]() , que se puede caracterizar según su término general,
, que se puede caracterizar según su término general,
| (1) |
No siempre es posible encontrar el termino general de una sucesión, a veces puede ser muy complicado. Si conseguimos encontrar el término general de una sucesión, decimos que la hemos resuelto.
En algunos casos, es más cómodo dar una regla que nos permita encontrar el valor del término n-ésimo a partir de los términos anteriores, lo que llamamos relación de recurrencia. Por ejemplo, podemos definir la sucesión de los números pares mediante la relación de recurrencia
| (2) |
este método nos obliga a dar información adicional sobre los primeros términos de la sucesión. En este ejemplo, nos es suficiente con especificar
La sucesión de Fibonacci es aquella en que cada término es la suma aritmética de los dos anteriores, es decir, viene definida por la relación de recurrencia
donde tenemos que especificar los valores de
Otra elección de los primeros términos conducirá, naturalmente, a una sucesión de Fibonacci diferente.
Uno de los hechos más conocidos de la sucesión de Fibonacci es que el cociente de dos de sus términos consecutivos tiende al número áureo,
![]() , a medida que
, a medida que ![]() crece, es decir,
crece, es decir,
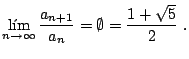 |
(4) |
Además, la convergencia a este límite es alternada, es decir, si un término de acerca al límite por arriba, el siguiente se acercará por debajo, y viceversa.
La sucesión de Fibonacci aparece en diversos fenómenos naturales, como son la reproducción de los conejos [1], la distribución de escamas de una piña [2], en el estudio de las leyes mendelianas de la herencia, etc.
2 Métodos operacionales de la mecánica cuántica
El concepto matemático de operador es de aplicación en prácticamente todas las ramas de la matemática y la física, siendo la mecánica cuántica la rama de la física donde más importancia intrínseca adoptan.
En general, un operador es un objeto matemático que actúa sobre otros objetos matemáticos de cierto tipo, transformandolos en otro objeto --en general, diferente-- de ese mismo tipo. Las funciones de una variable pueden ser consideradas como operadores, ![]() , que actúan sobre un número real,
, que actúan sobre un número real, ![]() , para dar otro número real,
, para dar otro número real, ![]() . Otro ejemplo común en la física y en la tecnología son las transformadas integrales, como la de Fourrier,
. Otro ejemplo común en la física y en la tecnología son las transformadas integrales, como la de Fourrier,
![]() o la de Laplace,
o la de Laplace,
![]() , que transforman una función
, que transforman una función ![]() en otra función diferente,
en otra función diferente,
![]() (en el caso de Laplace).
(en el caso de Laplace).
En mecánica cuántica, los operadores se aplican sobre los elementos, kets, de un espacio vectorial de Hilbert, que suelen se suelen indicar de la forma
![]() . Estos kets contienen toda la información física posible sobre el estado del sistema, incluyendo la denominada función de onda.Un operador
. Estos kets contienen toda la información física posible sobre el estado del sistema, incluyendo la denominada función de onda.Un operador ![]() transforma un estado o ket en otro diferente,
transforma un estado o ket en otro diferente,
| (5) |
Esto se aprovecha en mecánica cuántica para definir operadores que implementen las diferentes acciones que se pueden efectuar sobre un sistema físico, como puede ser medir algunas de sus características, realizar transformaciones de simetría, etc.
3 Métodos operacionales y la sucesión de Fibonacci
Siguiendo la filosofía de la utilización de operadores que hemos visto en el apartado anterior, vamos intentar hallar el término general de la sucesión de Fibonacci utilizando para ello los conceptos de los métodos operacionales.
Definimos el operador siguiente, ![]() , que aplicado al término n-ésimo de la sucesión de Fibonacci nos envuelve el siguiente,
, que aplicado al término n-ésimo de la sucesión de Fibonacci nos envuelve el siguiente,
| (6) |
Mediante este operador, podemos encontrar el término n-ésimo de la sucesión mediante la aplicación reiterada,
por tanto, caracterizando el operador
Para encontrar la solución al término general de la sucesión de Fibonacci reescribiremos la relación de recurrencia que define la sucesión, ecuación (3), en el lenguaje del operador ![]() ,
,
| (8) |
o bien, reordenando términos y sacando factor común tenemos
| (9) |
o lo que es lo mismo
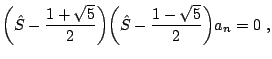 |
(10) |
vemos como, por primera vez, aparece de forma natural el número áureo. Por lo tanto, tenemos dos posibles soluciones posibles para el operador
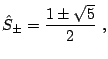 |
(11) |
que, aplicadas a la expresión del termino general, ec. (7), tenemos
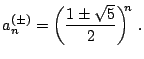 |
(12) |
Dado que tenemos dos soluciones posibles, la solución más general será una combinación lineal de las dos posibilidades,
Las constantes
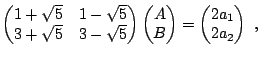 |
(14) |
i, naturalmente, la solución se puede encontrar invirtiendo la matriz
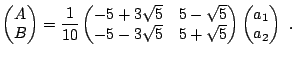 |
(15) |
En el caso más habitual,
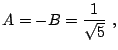 |
(16) |
con lo que la solución final al término general de la ecuación de Fibonacci para este caso más particular se escribe de la forma
![$\displaystyle a_n = \frac{1}{\sqrt{5}} \left[ \bigg( \frac{1 + \sqrt{5}}{2} \bigg)^{\!\!n} - \bigg( \frac{1 - \sqrt{5}}{2} \bigg)^{\!\!n} \right] .$](img41.png) |
(17) |
Podemos simplificar esta última ecuación mediante el desarrollo del binomio de Newton,1
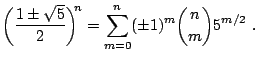 |
(18) |
Substituyendo directamente, obtenemos
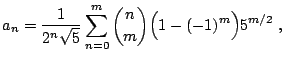 |
(19) |
por tanto, tan sólo contribuyen los términos con
![$\displaystyle a_n = \frac{1}{2^{n-1}} \sum_{k=0}^{\left[(n-1)/{2}\right]} {n \choose 2k+1} 5^{k} ,$](img48.png) |
(20) |
donde
Para comprobar la validez de la fórmula general, ec. (13), podemos utilizar los resultados obtenidos para calcular otra sucesión de Fibonacci, por ejemplo la ![]() y
y ![]() , el resultado obtenido es
, el resultado obtenido es
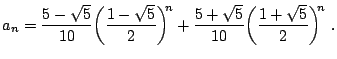 |
(21) |
En la ecuación anterior no es evidente que
![$\displaystyle \frac1{2^n} \sum_{k=0}^{\left[n/2\right]} {n \choose 2k} 5^k$](img59.png) |
|||
![$\displaystyle + \frac1{10\cdot2^{n-1}} \sum_{k=1}^{\left[(n+1)/2\right]} {n \choose 2k-1} 5^k ,$](img60.png) |
(22) |
4 El número de oro
Tal y como hemos dicho anteriormente, el cociente de dos términos consecutivos de la sucesión de Fibonacci tiende al número de oro, de forma alternada. En esta sección veremos que, una vez encontrada la fórmula general ec. (13), demostrar esta afirmación es trivial, y la demostración es válida para cualquier sucesión del tipo de Fibonacci.
Podemos expresar lo dicho de forma matemica definiendo una nueva sucesión, ![]() , como el cociente de dos términos consecutivos de la sucesión de Fibonacci, es decir,
, como el cociente de dos términos consecutivos de la sucesión de Fibonacci, es decir,
| (23) |
El límite de esta nueva sucesión, para
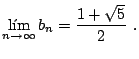 |
(24) |
Teniendo en cuenta la expresión general de ![]() , para cualquier sucesión de Fibonacci, ec. (13), podemos expresar el término general de
, para cualquier sucesión de Fibonacci, ec. (13), podemos expresar el término general de ![]() de forma trivial,
de forma trivial,
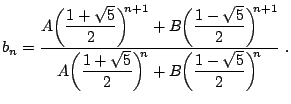 |
(25) |
Dado que
![]() es --en valor absoluto-- menor que la unidad, el término que lo contiene tendirá muy rápidamente a cero a medida que el valor de
es --en valor absoluto-- menor que la unidad, el término que lo contiene tendirá muy rápidamente a cero a medida que el valor de ![]() crece. Por lo tanto, en el límite
crece. Por lo tanto, en el límite
![]() podemos ignorar todos los términos que contienen esta cantidad. Por tanto,
podemos ignorar todos los términos que contienen esta cantidad. Por tanto,
tal y como esperábamos.
Más sutil es demostrar que la convergencia al número de oro es alternada, es decir, que si ![]() es mayor que el número de oro, tanto
es mayor que el número de oro, tanto ![]() como
como ![]() son menores, y viceversa.
son menores, y viceversa.
Para realizar esta demostración debemos calcular el término subdominante de este límite. Será útil tener en cuenta que, para valores de ![]() pequeños en comparación con la unidad, se tiene la aproximación
pequeños en comparación con la unidad, se tiene la aproximación
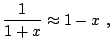 |
(27) |
donde se ignoran términos de orden
Para simplificar la notación, definimos
![]() . Aplicando el desarrollo anterior a la ecuación (26) tenemos, para
. Aplicando el desarrollo anterior a la ecuación (26) tenemos, para ![]() altas,
altas,
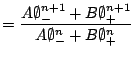 |
(28) | |
![$\displaystyle = \dfrac{ \emptyset_+^{n+1} \left[ 1 + \frac AB \left( \frac{\emp...
...[ 1 + \frac AB \left( \frac{\emptyset_-}{\emptyset_+} \right)^{\!\!n} \right] }$](img76.png) |
(29) | |
![$\displaystyle \approx \emptyset_+ \left[ 1 + \frac AB \left( \frac{\emptyset_-}...
...ft[ 1 - \frac AB \left( \frac{\emptyset_-}{\emptyset_+} \right)^{\!\!n} \right]$](img77.png) |
(30) | |
![$\displaystyle \approx \emptyset_+ \left[ 1 + \frac AB \left( \frac{\emptyset_-}...
...frac AB \left( \frac{\emptyset_-}{\emptyset_+} \right)^{\!\!n} + \cdots \right]$](img78.png) |
(31) | |
![$\displaystyle = \emptyset_+ \left[ 1 - \frac AB \left( \frac{\emptyset_-}{\empt...
...)^{\!\!n} \left\{ 1 - \frac{\emptyset_-}{\emptyset_+} \right\} + \cdots \right]$](img79.png) |
(32) |
donde en el último paso hemos despreciado el término cruzado, ya que sería un infinitesimal de orden superior. Dado que el cociente
5 Conclusiones
En este artículo hemos visto como los métodos operacionales usados, entre otras ramas de la física, por la mecánica cuántica, resultan de gran utilidad en un problema que, aparentemente, no tiene ninguna relación con ello. Estos métodos nos han permitido obtener la fórmula del término general de cualquier sucesión de Fibonacci, donde podemos escoger los dos términos de la sucesión.Además, hemos comprovado que las relaciones existentes entre la sucesión de Fibonacci y el número de oro se pueden comprobar trivialmente a partir de la fórmula general obtenida.
Bibliografía
-
- 1
-
El número de oro. (página web) Dirección url:
http://centros5.pntic.mec.es/cpr.de.aranjuez/foro/circo/fibonac.htm . - 2
-
Sucesión de Fibonacci y la razón áurea. (página web) Dirección url:
http://www.geocities.com/Athens/Acropolis/ 4329/fibo_au.htm - 3
-
La sucesión de Fibonacci. (página web) Dirección url:
http://www.geocities.com/Athens/Acropolis/4329 /fibonac.htm


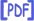
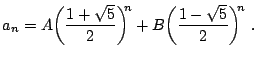
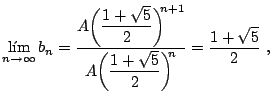
 donde
donde