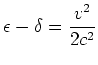Bájatelo LaTeX Post-script Portable Document Format

MICHELSON'S INTERFERENCE EXPERIMENT

H. A. Lorentz


Date: year 1895

1 The experiment

As Maxwell first remarked and as follows from a very simple calculation, the time required by a ray of light to travel from a point $ A$ to a point $ B$ and back to $ A$ must vary when the two points together undergo a displacement without carrying the ether with them. The difference is certainly, a magnitude of second order; but it is sufficiently great to be detected by a sensitive interference method.

The experiment was carried out by Michelson in 1881.1 His apparatus, a kind of interferometer, had two horizontal arms $ P$ and $ Q$ , of equal length and at right angles one to the other. Of the two mutually interfering rays of light the one passed along the arm $ P$ and back, the other along the arm $ Q$ and back. The whole instrument, including the source of light and the arrangement for taking observations, could be revolved about a vertical axis; and those two positions come specially under consideration in which the arm $ P$ or the arm $ Q$ lay as nearly as possible in the direction of the Eart's motion. On the basis of Fresnel's theory it was anticipated that when the apparatus was revolved from on of these principal positions into the other there would be a displacement of the interference fringes.

But of such a displacement -for the sake of brevity we will call it the Maxwell displacement- conditioned by the change in the times of propagation, no trace was discovered, and accordingly Michelson thought himself justified including that while de Earth is moving, the ether does not remain at rest. The correctness of this inference was soon brought into question, for by an oversight Michelson had taken the change in the pase difference, which was to be expected in accordance with the theory, at twice its proper value. If we make the necessary correction, we arrive at displacements no greater than might be masked by errors of observation.

Subsequently Michelson2 took up the investigation anew in collaboration with Morley, enhancing the delicacy of the experiment by causing each pencil to be reflected to and from between a number of mirrors, thereby obtaining the same advantage as if the arms of the eariler apparatus had been considerably lengthened. The mirrors were mounted on a massive stone disc, floating on mercury, and thereforce easily revolved. Each pencil now had to travel a total distance of $ \unit{22} \meter$ , and n Fresnel's theory the displacement to be expected in passing from the one principal position to the other would be $ 0,4$ of the distance between the interference fringes. Nevertheless the rotation produced displacements not exceeding $ 0,02$ of this distance, and these might well be ascribed to errors of observation.

Now, does this result entitle us to assume that the ether takes part in the motion of the Earth, and thereforce that the theory of aberration given by Stokes is the correct one? The difficulties which this theory encounters in explaining aberration seem too great for me to share this opinion, and I would rather try to remove the contradiction between Fresnel's theory and Michelson's result. An hypothesis which I brought forward some time ago,3 and which, as I subsequently learned, has also ocurred to Fitzgerald, 4 enables us to do this. The next paragraph will set out this hypothesis.

2 The contraction hypothesis

To simplify matters we will assume that we are working with apparatus as employed in the first experiments, and that in the one principal position the arm $ P$ lies exactly in the direction of the motion of the Eart. Let $ v$ be the velocity of this motion, $ L$ the length of either the arm, and hence $ 2L$ the path traversed by the rays of light. According to the theory,5 the turning of the pencil travels along $ P$ and back to be longer than the time which the other pencil takes to complete its joourney by

$\displaystyle \frac{Lv^{2}}{c^{3}}$    

There would be this same difference if the translation had no influence and the arm $ P$ were longer than the arm $ Q$ by $ \frac{Lv^{2}}{2c^{2}}$ . Similarly with the second principal position.

Thus we see that the phase differences expected by the theory might also arise if, when the apparatus is revolved, first the one arme and then the other arm were the longer. If follows that the phase differences can be compensated by contrary changes of the dimensions.

If we assume the arm which lies in the direction of the Eart's motion to be shorter than the other by $ \frac{Lv^{2}}{c^{2}}$ , and, at the same time, that the translation has the influence which Fresnel's theory allows it, then the result of the Michelson experiment is explained completely.

Thus one would have to imagine that the motion of a solid body(such as a brass rod or the stone disc employed in the later experiments) through the resting ether exerts upon the dimensions of that body an influence which varies according to the orientation of the body with respect to the direction of motion. If, for example, the dimensions parallel to this direction were changed in the proportion of $ 1$ to $ 1+\delta$ , and those perpendicular in the proportion of $ 1$ to $ 1 + \epsilon$ , then we should have the equation

$\displaystyle \epsilon - \delta = \frac{v^{2}}{2c^{2}}$ (1)

in which the value of one of the quantities $ \delta$ and $ \epsilon$ would remain undetermined. If might be that $ \epsilon = 0$ , $ \delta = - \frac{v^{2}}{2c^{2}}$ , but also $ \epsilon = \frac{v^{2}}{2c^{2}}$ , $ \delta=0$ , or $ \epsilon = \frac{v^{2}}{2c^{2}}$ , and $ \delta = - \frac{v^{2}}{2c^{2}}$ .

3 The contraction in relation to molecular forces I

Surprising as this hypothesis may appear at first sight, yet we shall have to admit that it is by no means far-fetched, as soon as we assume that molecular forces are also transmitted through the ether, like the electric and magnetic forces of which we are able at the present time to make this assertion definitely. If they are so transmitted, the translation will ver probably affect the action between two molecules or atoms in a manner resembling the attraction or repulsion between charged particles. Now, since the form and dimensions of a solid body are ultimately conditioned by the intensity of molecular actions, there cannot fail to be a charge of dimensions as well.

From the theoretical side, therefore, there would be no objection to the hypothesis. As regards its experimental proof, we must first of all note that the lenghtenings and shortenings in question are extraordinarily small. We have $ v^{2}/c^{2} = 10^{-8}$ , and thus, if $ \epsilon = 0$ , the shortening of the one diameter of the Earth would amount to about $ \unit{6,5} \centi\meter$ . The lenght of a meter rod would change, when moved from one principal position into the other, by about $ \unit{200^{-1}}\micro\meter$ . One could hardly hope for success in trying to perceive such small quantities except by means of an interference method. We should have to operate with two perpendicular rods, and with two mutually interfering pensils of light, allowing the one to travel to and from along the first rod, and the other along the second rod. But in this way we should come back once more to the Michelson experiment, and revolving the apparatus we should perceive no displacement of the fringes. Reversing a previous remark, we might now say that the displacement produced by the alternations of length is compensated by the Maxwell displacement.

4 The contraction in relation to molecular forces II

It is worth noticing that we are led to just the same changes of dimensions as have been presumed above if we, firstly, without taking molecular movement into consideration, assume that in a solid body left to itself the forces, attractions or repulsions, acting upon any molecule maintain one another equilibrium, and, secondly -though to be sure, there is no reason for doing so- if we apply to these molecular forces the law which is another place6 we deduced for electrostatics actions. For if we now understand by $ S_{1}$ and $ S_{2}$ not, as formerly, two systems of charged particles, but tow systems of molecules -the second at rest and the first moving with a velocity $ v$ in the direction of the axis of $ x$ - between the dimensions of which the relationship subsutst as previously stated; and if we assume that in both systems the $ x$ components of the forces are the same, while the $ y$ and $ z$ components differ from one another by the factor $ \sqrt{1 - v^{2}/c^{2}}$ , then it is clear that the forces in $ S_{1}$ will be in equilibrium whenever they are so in $ S_{2}$ . If thereforce $ S_{2}$ is the state of equilibrium of a solid body at rest, then the molecules in $ S_{1}$ have precisely those positions in which they can persist under the influcence of translation. The displacement would naturally bring about this disposition of the molecules of its own accord, and thus effect shortening in the direction of motion in the proportion of $ 1$ to $ \sqrt{1 - v^{2}/c^{2}}$ , in accordance with the formula given in the above-mentioned paragraph. This leads to the values

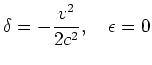$\displaystyle \delta = - \frac{v^{2}}{2c^{2}}, \quad \epsilon = 0$    

in agreement with (1).

In reality the molecules of a body are not at rest, but in every ``state of equilibrium'' there is a stationary movement. What influence this circumstante may have in the phenomenon which we have been considering is a question which we do not here touch upon; in any case the experiments of Michelson and Morley, in consequence of unavoidable errors of observation, afford considerable latitude for the values of $ \delta$ and $ \epsilon$ .

Footnotes

... 1881.1
Michelson, American Journal of Science, 22,1881, p.120
... Michelson2
Michelson and Morley, American Journal of Science, 34, 1887, p.333; Phil. Mag., 24, 1887, p.449.
... ago,3
Lorentz, Zittingaverslagen der Akad. v. We. te Amsterdam, 1892-93, p.74.
... Fitzgerald,4
As Fitzgerald kindly tells me, he has for a long time dealt with his hypothesis in his lectures. The only published reference which I can find to the hypothesis is by Lodge, ``Aberration Problems'' Phill. Trans. R.S., 184 A, 1893.
... theory,5
Cf. Lorentz, Arch. Néer., 2, 1887, pp. 168-176.
... place6
Viz., §23 of the book, "Versuch einer Theories der elektrischen und optischen Erscheinungen in bewegten Körperu."
Volver a la página principal
Acceso rápido Desactivar menú flotante
© 2003—2024, La web de Física
Dirección de contacto
Créditos