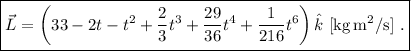Sobre una partícula de 3 kg actúa una fuerza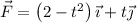 
(N). En el instante t = 0 la partícula se encuentra en el punto (4, 1) m, moviéndose con una velocidad 
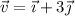(m/s), determinar al cabo de 1 s:
1.la posición de la partícula
2.el momento lineal y el momento angular de la partícula respecto al origen.
La segunda ley de Newton nos dice que
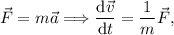
lo que nos da el siguiente sistema de ecuaciones
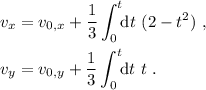
Integrando, tenemos
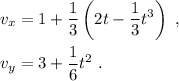
La posición se encuentra integrando una vez más,
lo cual nos da
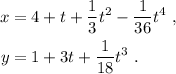
Es decir,
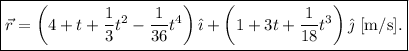
El momento lineal (o cantidad de movimiento) se define como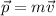 
. Leyendo directamente de (3),
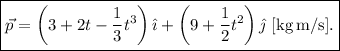
Por otra parte, el momento angular se escribe como un producto vectorial,
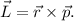
En general, deberíamos hacer el determinante completo para encontrar el producto vectorial. pero en este caso podemos simplificarlo usando la propiedad
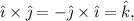
además de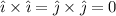 
. Usando esto, tenemos
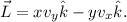
Retomando los resultados anteriores,
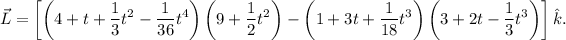
Operando,
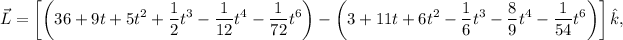
con lo cual, tenemos
