Hallar el trabajo hecho por la fuerza 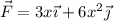 para elevar un punto material desde el origen hasta el punto (2, 4) m:
para elevar un punto material desde el origen hasta el punto (2, 4) m:
1.a lo largo de la recta 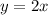 .
.
2.a lo largo de la curva 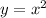 .
.
Para calcular el trabajo hecho por la fuerza, procederemos de la siguiente forma:
Calcularemos el trabajo infinitesimal, que es el producto escalar del vector fuerza por el vector desplazamiento, es decir:
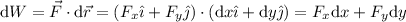
Las variables x e y están relacionadas a través de la ecuación de la trayectoria, cuya forma general es: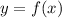 , y que en este caso, distinguiremos entre
, y que en este caso, distinguiremos entre 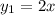 e
e 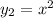 . Por tanto:
. Por tanto:
A lo largo de la recta 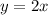
En este caso, tenemos que:
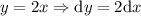
Por tanto, el trabajo infinitesimal será:
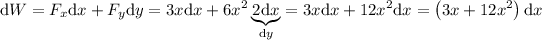
Así pues, el trabajo realizado por la fuerza para elevar el punto a lo largo de la recta es:
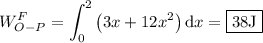
A lo largo de la curva 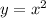 .
.
Procedemos de manera similar al anterior apartado, teniendo en cuenta en este caso que:
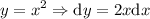
Por tanto, el trabajo infinitesimal será:
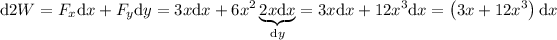
Por último, calculamos el trabajo realizado:
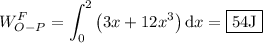
Observamos que el trabajo realizado por la fuerza para elevar el punto material hasta el punto P(2,4) a lo largo de la recta es mayor que el realizado a lo largo de la curva. Es decir, el trabajo depende del camino seguido para ir del punto O(0,0) al punto P(2,4).
De esto, podemos extraer la siguiente conclusión: la fuerza 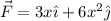 es una fuerza no conservativa, pues el trabajo depende del camino seguido para ir de un punto A a otro punto B.
es una fuerza no conservativa, pues el trabajo depende del camino seguido para ir de un punto A a otro punto B.
Podemos comprobar que la fuerza no es conservativa calculando el rotacional del campo de fuerzas:
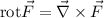
Podemos hallarlo mediante el siguiente determinante (nótese que éste es sólo simbólico):
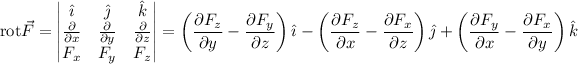
Por tanto:
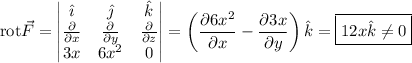
Dado que el rotacional es distinto de cero, la fuerza no es conservativa, tal y como habíamos determinado al observar que el trabajo realizado por la fuerza entre dos puntos dependía de la trayectoria seguida.


