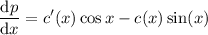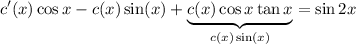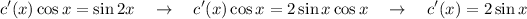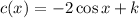Encontrar la solución general de las siguientes ecuaciones diferenciales.
1.
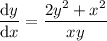
2.
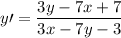
3.
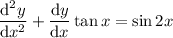
4.
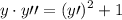
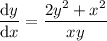
Esta ecuación 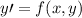 es una ecuación diferencial ordinaria de primer grado homogénea, éstas se definen como
es una ecuación diferencial ordinaria de primer grado homogénea, éstas se definen como 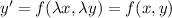 . Comprovemos que esta ecuación es homogénea:
. Comprovemos que esta ecuación es homogénea:
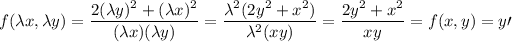
.
Las ecuaciones diferenciales homogéneas son del tipo 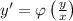 , con lo cual, un cambio útil es
, con lo cual, un cambio útil es
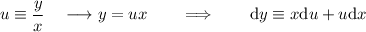
Lo aplicamos a (1) y nos queda
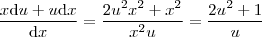
Y lo que nos queda es una ecuación con variables separables:
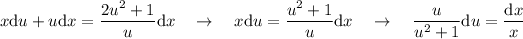
Integrando nos queda que
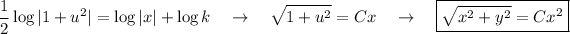
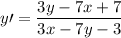
Cuando tenemos una ecuación diferencial del estilo 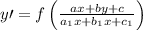 podemos imaginar que en el numerador y en el denominador tenemos la ecuación de dos rectas, sabemos que si
podemos imaginar que en el numerador y en el denominador tenemos la ecuación de dos rectas, sabemos que si
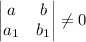
dichas rectas se cortan en un punto, es decir, el sistema formado por sus ecuaciones es compatible determinado. El procedimiento a seguir es, primero de todo resolver el sistema y encontrar el punto, luego trasladar los ejes a ese punto, es decir, hacer un cambio de coordenadas que analíticamente se puede entender como un cambio de variable:
el cambio que debemos realizar es
Si aplicamos el cambio a (7) nos queda que:
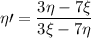
que (se puede comprobar) es una ecuación homogénea, con lo cual, el cambio [ERROR DE LaTeX. Error: 4 ] es el mejor para proceder:
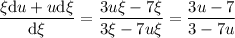
que es ya una ecuación de variables separables. Reordenando nos queda
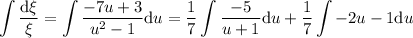
la segunda integral era una integral racional. Finalmente nos queda
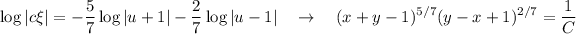
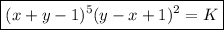
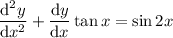
En este caso tenemos una ecuación del estilo 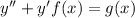 , podemos hacer el cambio
, podemos hacer el cambio 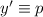 y nos queda
y nos queda
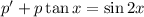
que es una ecuación diferencial lineal de primer orden. La resolveremos de la siguiente manera
Ahora regresamos a (18)
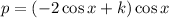
si deshacemos el cambio 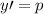 nos queda que
nos queda que
Aplicando algunas identidades trigonométricas
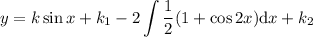
finalmente
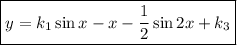
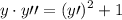
Tenemos una ecuación lineal en la que falta la  , es decir
, es decir 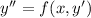
Haremos el siguiente cambio de variable
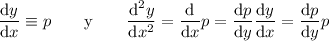
Aplicamos estos cambios a (26) y nos queda
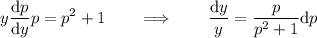
que tras integrar
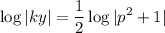
por conveniencia y para ahorrar notación hemos introducido la constante dentro del logaritmo 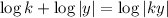 .
.
Trabajando un poco la expresión
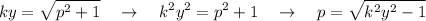
y deshaciendo el cambio de variable llegamos a una expresión integrable
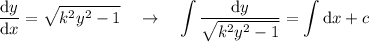
La primera integral se puede mirar en cualquier libro de tablas, 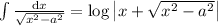 , es decir
, es decir
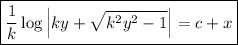
Podemos simplificar esta expresión escribiendo anulando los logaritmos con exponenciales y trabajando un poco la expresión nos queda que
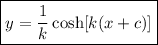

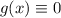 ).
).
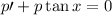

 como una función
como una función 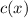 , método que se conoce como
, método que se conoce como