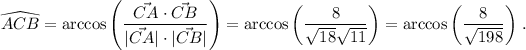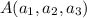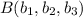La distancia entre dos puntos cualesquiera y es igual al módulo del vector cuyo inicio está en uno de los puntos y cuyo extremo está en el otro. Tomemos dicho vector 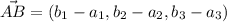(nótese que el resultado sería el mismo si consideráramos el vector 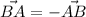). El módulo, que se representa por 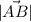, viene dado por la expresión:

(1)

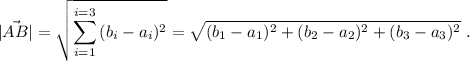
Por lo tanto, en el caso particular que se nos pide, la distancia entre los puntos 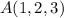y vendrá dada por (1), es decir

(2)

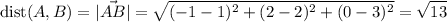
Dados tres puntos 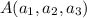, 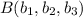y 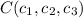, distintos entre sí; Si tomamos estos puntos como vértices de un triángulo 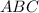, el ángulo 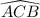de ese triángulo será igual al ángulo formado por los vectores 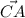y .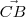

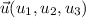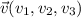El producto escalar de dos vectores no nulos cualesquiera y es igual a

(3)

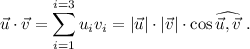
Así, el ángulo entre esos dos vectores será

(4)

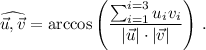
Por lo que en nuestro caso particular, el ángulo 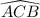será

(5)