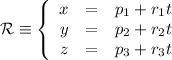Problemas de geometría lineal y espacio afín
Tomamos uno de los cuatro puntos como origen, por ejemplo D. Una vez fijado el origen, los otros tres puntos definen otros tantos tres vectores,
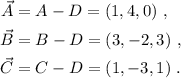
Estos tres vectores definen una matriz,
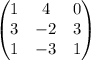
Si el rango de esta matriz es 1, entonces los cuatro puntos están alineados. Si el rango es 2, son coplanares. Si es tres, no son coplanares.
Podemos comprobar fácilmente que el rango es, como mínimo, dos considerando el menor
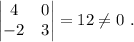
Nos queda únicamenmte comprobar si el rango de la matriz puede ser tres, calculando el determinante total,
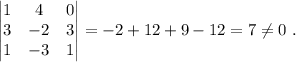
Por lo tanto, el rango de la matriz es tres, y los vectores no son coplanarios.
Dados los planos
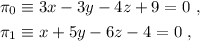
hallar la ecuación de la recta 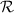 que pasa por el punto
que pasa por el punto 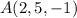 y es paralela a los dos planos.
y es paralela a los dos planos.
El vector perpendicular al plano 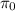 es
es 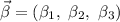 , mientras que el vector perpendicular a la recta
, mientras que el vector perpendicular a la recta 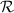 es
es 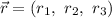 . La proyección del vector
. La proyección del vector 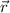 sobre
sobre 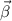 viene dada por el producto escalar,
viene dada por el producto escalar,
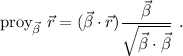
La proyección del vector 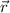 sobre el plano se obtiene restándole su proyección sobre el vector
sobre el plano se obtiene restándole su proyección sobre el vector 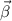 ,
,
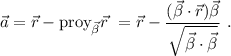
Para asegurarnos que la recta 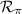 es la proyección sobre el plano de la recta
es la proyección sobre el plano de la recta 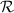 , debemos asegurarnos de que pasa por el punto de intersección entre la recta y el plano. Dicho punto se obtiene por simple substitución en la ecuación del plano de la ecuación de la recta,
, debemos asegurarnos de que pasa por el punto de intersección entre la recta y el plano. Dicho punto se obtiene por simple substitución en la ecuación del plano de la ecuación de la recta,
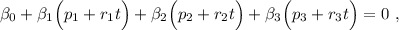
para facilitar el proceso, agrupamos todos los términos dependientes y los independientes, utilizando la notación del producto escalar, tenemos
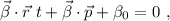
lo que nos da
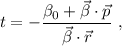
con lo que el punto de intersección será
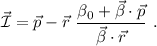
Por lo tanto, la ecuación de la recta 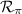 será
será
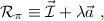
lo que nos da
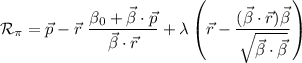
Una recta viene dada por dos puntos, en este caso, como la recta pedida, 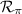 es la proyección de la recta
es la proyección de la recta 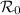 sobre el plano
sobre el plano 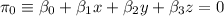 usaremos el punto intersección de
usaremos el punto intersección de 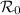 y
y 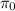 ; lo llamaremos
; lo llamaremos 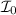 . El segundo punto de la recta,
. El segundo punto de la recta, 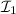 , lo obtendremos al proyectar otro cualquiera de la recta
, lo obtendremos al proyectar otro cualquiera de la recta 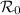 ,
, 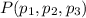 sobre
sobre 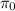 . Esto lo haremos usando una recta
. Esto lo haremos usando una recta 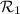 , perpendicular al plano
, perpendicular al plano 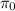 y que pase por
y que pase por 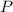 ;
; 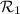 tendrá la dirección de
tendrá la dirección de 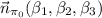 .
.
Para calcular la intersección de 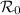 y
y 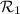 con
con 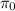 seguiremos el siguiente método. Sea la recta
seguiremos el siguiente método. Sea la recta 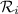 .
.
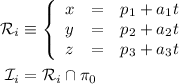
Donde para 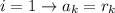 y para
y para 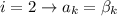 .
.
Si expresamos 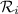 de forma continua
de forma continua
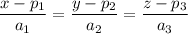
Y ahora resolvemos dos de las tres igualdades, entonces podemos expresarla como intersección de dos planos
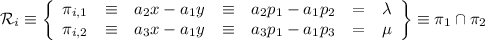
Así podemos reescribir la segunda ecuación de [ref]61[/tex] como 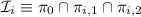 . Para calcular ahora las coordenadas de
. Para calcular ahora las coordenadas de 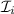 no tenemos, pues, más que resolver el siguiente sistema, que es compatible determinado:
no tenemos, pues, más que resolver el siguiente sistema, que es compatible determinado:
Donde 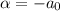 ,
, 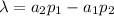 y
y 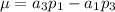 . Lo resolveremos mediante la REGLA DE CRAMER, por lo que:
. Lo resolveremos mediante la REGLA DE CRAMER, por lo que:
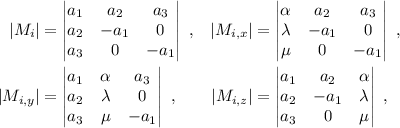
Así, tenemos que 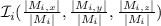 . Que es el punto intersección de
. Que es el punto intersección de 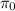 y
y 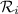 .
.
Una vez obtenidos 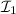 e
e 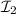 , la recta buscada,
, la recta buscada, 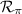 , es la que tiene como vector dirección al vector
, es la que tiene como vector dirección al vector
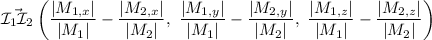
Y pasa por cualquier punto 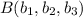 perteneciente al plano
perteneciente al plano 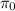 . Entonces podremos escribir
. Entonces podremos escribir 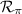 en forma general como sigue
en forma general como sigue
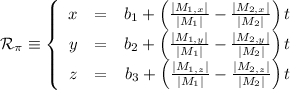
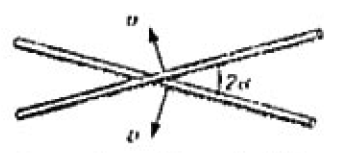
Dos barras se cruzan bajo un ángulo  y se mueven con iguales velocidades
y se mueven con iguales velocidades  y perpendicularmente a si mismas, tal como se indica en la figura. ¿Cuál será la velocidad del punto de cruce de las barras?
y perpendicularmente a si mismas, tal como se indica en la figura. ¿Cuál será la velocidad del punto de cruce de las barras?

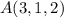 y es perpendicular a la recta
y es perpendicular a la recta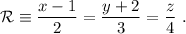

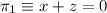 y
y 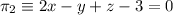 .
.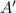 , del punto
, del punto 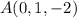 respecto del plano
respecto del plano 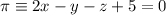 .
.