Problemas de integración
Aunque parece que el problema se ha de resolver con la aplicación de algún teorema rebuscado, se puede aplicar (con la ayuda de cierta picardía) el método de integración por partes.
En primer lugar, calcularemos la integral indefinida asociada, separando nuestra integral en dos
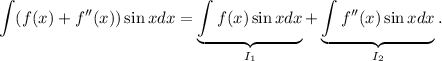
Para expresar 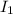 de otra manera, haremos uso del método de integración por partes
de otra manera, haremos uso del método de integración por partes
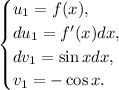
es decir
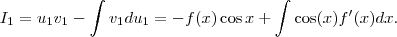
Hacemos lo mismo con 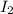 , con una asignación algo diferente
, con una asignación algo diferente
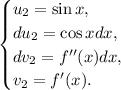
o sea
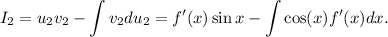
De esta manera
donde se ha añadido la constante de integración 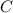 .
.
Aplicando finalmente la regla de Barrow
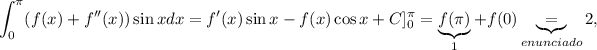
y concluimos que
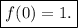
Sean las integrales
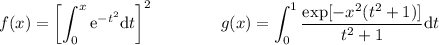
1.Demostrad que 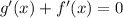 y que
y que 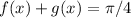
2.A continuación,teniendo en cuenta que 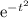 es una función con simetría par,utilizad este resultado para mostrar que
es una función con simetría par,utilizad este resultado para mostrar que
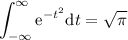
Sea la función 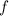 definida mediante
definida mediante
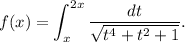
Estudiar las asíntotas y la monotonía de 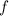 . Dibujar aproximadamente la gráfica de
. Dibujar aproximadamente la gráfica de 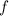 .
.

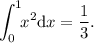

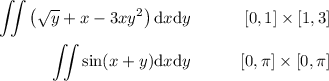
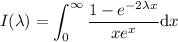
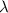 (siendo
(siendo 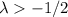 )
)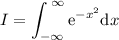
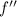 es continua y que
es continua y que 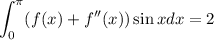 . Sabiendo que
. Sabiendo que 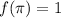 , calcule
, calcule 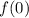 .
.