Problemas de Álgebra vectorial
Nivel: Secundaria
Dados los vectores 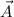 y
y 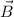 con origen en el punto común
con origen en el punto común 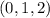 y extremos A(-1,2,3) y B(2,-1,1) respectivamente, calcular:
y extremos A(-1,2,3) y B(2,-1,1) respectivamente, calcular:
1.Producto escalar  .
.
2.Producto vectorial 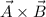 .
.
3.Producto vectorial 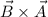 .
.
La velocidad de un móvil es 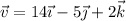 . Una fuerza
. Una fuerza 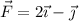 actúa sobre él. Calcula la componente de dicha fuerza en la dirección del movimiento y en la dirección perpendicular a él.
actúa sobre él. Calcula la componente de dicha fuerza en la dirección del movimiento y en la dirección perpendicular a él.
Dados los vectores 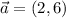 y
y 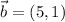 , calcula:
, calcula:
1.El producto escalar de ambos vectores.
2.La proyección de 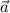 , sobre
, sobre 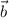
3.Las coordenadas de un vector unitario de la misma dirección que 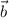
4.Un vector de la misma dirección que 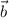 y cuyo módulo sea igual a la proyección de
y cuyo módulo sea igual a la proyección de 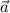 sobre
sobre 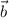 .
.
El producto escalar de dos vectores cualesquiera es igual a la suma del producto de sus coordenadas vstyrdisnsd una a una, es decir, sean 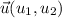 y
y 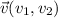 , en el plano su producto escalar es
, en el plano su producto escalar es 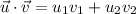 .
.
Así para los vectores dados tenemos que 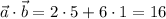 .
.
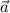 , sobre
, sobre 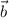
Se define la proyección de un vector 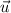 sobre otro
sobre otro 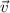 como
como 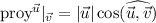 , a partir del producto escalar sabemos que
, a partir del producto escalar sabemos que 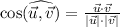 así podemos escribir que la proyección de un vector sobre otro es:
así podemos escribir que la proyección de un vector sobre otro es:
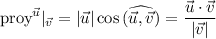
En el caso particular 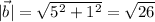 , entonces
, entonces 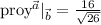 .
.
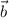
En el caso general un vector unitario 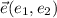 , paralelo a otro no nulo
, paralelo a otro no nulo 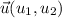 , tenemos que
, tenemos que 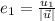 y
y 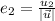 .
.
Para el caso particular y teniendo en cuenta que 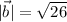 , el vector unitario
, el vector unitario 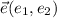 será
será 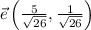 .
.
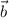 y cuyo módulo sea igual a la proyección de
y cuyo módulo sea igual a la proyección de 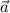 sobre
sobre 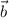 .
.En general y usando los resultados de apartados anteriores, sea 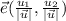 , donde
, donde 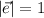 , y por las propiedades de los vectores, multiplicación por un escalar,
, y por las propiedades de los vectores, multiplicación por un escalar, 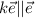 y
y 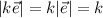 , si tomamos
, si tomamos 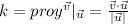 , tenemos que
, tenemos que
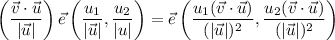
En particular siendo 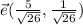 y
y 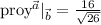 tenemos que
tenemos que
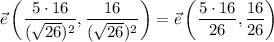
Dados dos vectores 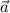 y
y 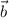 , obtener el vector proyección ortogonal de
, obtener el vector proyección ortogonal de 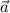 sobre
sobre 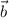 . Aplicarlo al caso en que [ERROR DE LaTeX. Error: 4 ] , [ERROR DE LaTeX. Error: 4 ] y
. Aplicarlo al caso en que [ERROR DE LaTeX. Error: 4 ] , [ERROR DE LaTeX. Error: 4 ] y 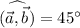 , obtener también la proyección ortogonal de
, obtener también la proyección ortogonal de 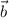 sobre
sobre 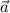 .
.
Halla el momento con respecto al punto P(0,-1,1) del vector unitario con origen en O(2,2,2) y que es paralelo al vector 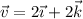 .
.


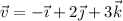 , halla otra de la misma dirección y sentido contrario, de módulo 3.
, halla otra de la misma dirección y sentido contrario, de módulo 3.