Problemas de geometría lineal y espacio afín
Dados los planos
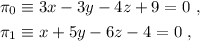
hallar la ecuación de la recta  que pasa por el punto
que pasa por el punto 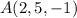 y es paralela a los dos planos.
y es paralela a los dos planos.
Dados el punto 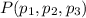 y el plano
y el plano 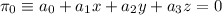 . El punto simétrico,
. El punto simétrico, 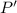 de
de 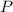 respecto de
respecto de 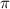 será el punto que cumpla
será el punto que cumpla
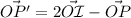
donde 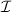 es el punto de intersección entre el plano
es el punto de intersección entre el plano 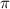 y la recta
y la recta 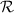 , perpendicular a éste y que pasa por
, perpendicular a éste y que pasa por 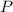 . Matemáticamente:
. Matemáticamente:
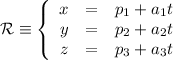
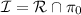
Si expresamos 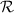 de forma continua
de forma continua
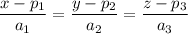
Y ahora resolvemos dos de las tres igualdades, podemos expresar  como intersección de dos planos
como intersección de dos planos
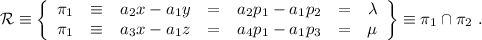
Así podemos reescribir (5.2) como 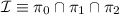 . Para calcular ahora las coordenadas de
. Para calcular ahora las coordenadas de 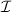 no tenemos, pues, más que resolver el siguiente sistema, que es compatible determinado:
no tenemos, pues, más que resolver el siguiente sistema, que es compatible determinado:
Donde 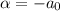 ,
, 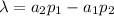 y
y 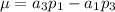 . Lo resolveremos mediante la REGLA DE CRAMER, por lo que:
. Lo resolveremos mediante la REGLA DE CRAMER, por lo que:
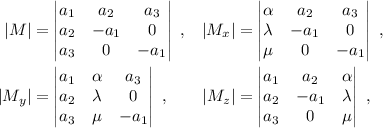
Así, tenemos que 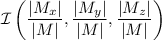 . Si ahora utilizamos este resultado en (1), obtenemos las coordenadas del punto simétrico
. Si ahora utilizamos este resultado en (1), obtenemos las coordenadas del punto simétrico  :
:
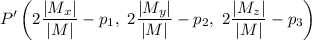
En partircular para el caso dado,
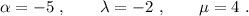
Por lo tanto,
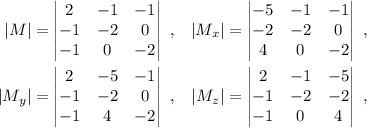
Entonces tenemos que
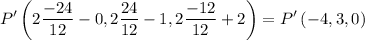
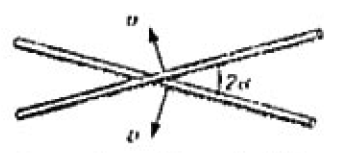
Dos barras se cruzan bajo un ángulo  y se mueven con iguales velocidades
y se mueven con iguales velocidades  y perpendicularmente a si mismas, tal como se indica en la figura. ¿Cuál será la velocidad del punto de cruce de las barras?
y perpendicularmente a si mismas, tal como se indica en la figura. ¿Cuál será la velocidad del punto de cruce de las barras?

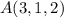 y es perpendicular a la recta
y es perpendicular a la recta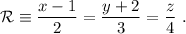

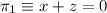 y
y 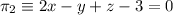 .
.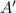 , del punto
, del punto 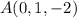 respecto del plano
respecto del plano 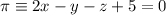 .
.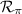 , proyección de la recta
, proyección de la recta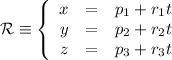
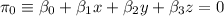 .
.