Problemas de campo magnético estático
Nivel: Primer ciclo
Una esfera sólida de masa 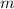 gira uniformemente alrededor de su eje con una carga
gira uniformemente alrededor de su eje con una carga 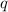 distribuida uniformemente en su superficie. Probar que el momento magnético
distribuida uniformemente en su superficie. Probar que el momento magnético 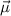 esta relacionado con el momento angular
esta relacionado con el momento angular 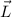 , por:
, por:
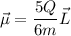
Para resolver este ejercicio consideraré el sistema de referencia en el centro de la esfera, y por la simetría que presenta esta usaré coordenadas esféricas, además no usaré notación vectorial, debido a que tanto el momento magnético como el momento angular están ubicados en una misma dirección.
Luego, como la carga está distribuida uniformemente en la superficie, solamente interesa analizar al cascarón exterior de la esfera sólida, y si a este lo divido en espiras pequeñitas, se tendrá que el momento magnético para cada una de estas es:
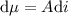
Donde 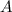 , es el área de la espira, y viene dada por:
, es el área de la espira, y viene dada por:
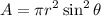
Además el diferencial de corriente, como es conocida la velocidad angular con la que gira la esfera será:
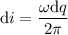
Y como esta cargada uniformemente, el cascarón tendrá una densidad superficial de carga:
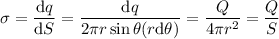
Con lo que se llega a que:
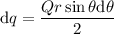
Luego juntando (2), (3) y (5) en (1), e integrando se tiene:
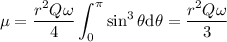
Finalmente tomando en cuenta que 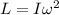 y que para una esfera sólida
y que para una esfera sólida 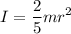 , la ecuación (6) se puede escribir como:
, la ecuación (6) se puede escribir como:
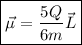
Un disco de radio 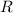 lleva una carga fija de densidad
lleva una carga fija de densidad 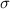 y gira con una velocidad angular
y gira con una velocidad angular 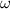 .
.
1.Halle la inducción magnética 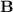 en un punto situado en el eje de simetría del disco a una distancia
en un punto situado en el eje de simetría del disco a una distancia  del centro.
del centro.
2.Halle la inducción magnética 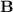 en el centro del disco.
en el centro del disco.
1.Un disco no conductor de pequeño grosor de masa 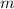 , uniformenente distribuida en toda la superficie del mismo, y radio
, uniformenente distribuida en toda la superficie del mismo, y radio 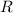 posee una densidad superficial de carga uniforme
posee una densidad superficial de carga uniforme 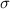 y gira con velocidad angular
y gira con velocidad angular 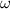 alrededor de su eje. Determine el momento (dipolar) magnético del disco en rotación.
alrededor de su eje. Determine el momento (dipolar) magnético del disco en rotación.
2.Una esfera sólida de radio 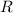 posee una densidad de carga uniforme
posee una densidad de carga uniforme 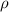 y una carga total
y una carga total 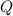 . La esfera gira alrededor de su diámetro con velocidad angular
. La esfera gira alrededor de su diámetro con velocidad angular 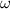 , y posee una masa total
, y posee una masa total 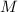 uniformenente distribuida en toda ella. Con la ayuda del resultado del apartado anterior, calcule el momento (dipolar) magnético de la esfera giratoria.
uniformenente distribuida en toda ella. Con la ayuda del resultado del apartado anterior, calcule el momento (dipolar) magnético de la esfera giratoria.
3.Para la esfera sólida, demuestre que los vectores de momento magnético y momento angular están relacionados por 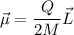 , resultado de validez general para cuerpos con densidades de carga y masa ambas uniformes, con
, resultado de validez general para cuerpos con densidades de carga y masa ambas uniformes, con 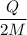 el denominado factor giromagnético.
el denominado factor giromagnético.


