Dr. phil. Copenhagen
(Received July 1913)
Introduction
In order to explain the results of experiments on scattering of ![]() rays by
matter Prof. Rutherford1has given a theory of the structure of atoms. According to this theory, the atom
consist of a positively charged nucleus surrounded by a system of electrons kept
together by attractive forces from the nucleus; the total negative charge of the
electrons is equal to the positive charge of the nucleus. Further, the nucleus
is assumed to be the seat of the essential part of the mass of the atom, and to
have linear dimensions exceedingly small compared with the linear dimensions of
the whole atom. The number of electrons in an atom is deduced to be
approximately equal to half the atomic weight. Great interest is to be
attributed to this atom-model; for, as Rutherford has shown, the
assumption of the existence of nuclei, as those in question, seems to be
necessary in order to account for the results of the experiments on large angle
scattering of the
rays by
matter Prof. Rutherford1has given a theory of the structure of atoms. According to this theory, the atom
consist of a positively charged nucleus surrounded by a system of electrons kept
together by attractive forces from the nucleus; the total negative charge of the
electrons is equal to the positive charge of the nucleus. Further, the nucleus
is assumed to be the seat of the essential part of the mass of the atom, and to
have linear dimensions exceedingly small compared with the linear dimensions of
the whole atom. The number of electrons in an atom is deduced to be
approximately equal to half the atomic weight. Great interest is to be
attributed to this atom-model; for, as Rutherford has shown, the
assumption of the existence of nuclei, as those in question, seems to be
necessary in order to account for the results of the experiments on large angle
scattering of the ![]() rays.2
rays.2
In an attempt to explain some of the properties of matter on the basis of this atom-model we meet, however, with difficulties of a serious nature arising from the apparent instability of the system of electrons: difficulties purposely avoid in atom-models previously considered, for instance, in the one proposed by Sir. J.J. Thomson3 According to the theory of the latter the atom consist of a sphere of uniform positive electrification, inside which the electrons move in circular orbits.
The principal difference between the atom-models proposed by Thomson and Rutherford consist in the circumstance that the forces acting on the electrons in the atom-model of Thomson allow of certain configurations and motion of the electrons for which the system is in a stable equilibrium; such configurations, however, apparently do not exist for the second atom- model. The nature of the difference in question will perhaps be most clearly seen by noticing that among the quantities characterizing the fist atom a quantity appears - the radius of the positive sphere - of dimensions of a length and of the same order of magnitude as the linear extension of the atom, while such a length does not appear among the quantities characterizing the second atom, viz. the charges and masses of the electrons and the positive nucleus; nor can it do determined solely by help of the latter quantities.
The way of considering a problem of this kind has, however, undergone essential alterations in recent years owing to the development of the theory of the energy radiation, and the direct affirmation of the new assumptions introduced in this theory, found by experiments on very different phenomena such as specific heats, photoelectric effect, , & c. The result of the discussion of these questions seems to be a general acknowledgment of the inadequacy of the classical elecrtodynamics in describing the behaviour of system of atomic size.4 Whatever the alteration in the laws of motion of the electrons may be, it seems necessary to introduce in the laws in question a quantity foreign to the classical electrodynamics, i.e., Planck's constant, or as it often is called the elementary quantum of action. By the introduction of this quantity the question of the stable configuration of the electrons in the atoms is essentially changed, as this constant is of such dimensions and magnitude that it, together with the mass and charge of the particles, can determine a length of the order of magnitude required.
This paper is an attempt to show that the application of the above ideas to Rutherford's atom-model affords a basis for a theory of the constitution of atoms. It will further be shown that from this theory we are led to a theory of the constitution of molecules.
In the present first part of the paper the mechanism of the binding of electrons by a positive nucleus is discussed in relation to Planck's theory. It will be shown that it is possible from the point of view taken to account in a simple way for the law of the line spectrum of hydrogen. Further, reason are given for a principal hypothesis on which the considerations contained in the following parts are based.
I wish here to express my thinks to Prof. Rutherford for his kind and encouraging interest in this work.
Part I. - Binding of Electrons by Positive Nuclei.
 . General Considerations
. General Considerations
The inadequacy of the classical electrodynamics in accounting for the properties of atoms from an atom-model as Rutherford's, will appear very clearly if we consider a simple system consisting of a positively charged nucleus of very small dimensions and an electron describing closed orbits around it. For simplicity, let us assume that the mass of the electron is negligibly small in comparison with that of the nucleus, and further, that the velocity of the electron is small compared with that of light.
Let us at first assume that there is no energy radiation.
In this case the electron will describe stationary elliptical orbits. The
frequency of revolution ![]() and the major-axis of the orbit
and the major-axis of the orbit ![]() will depend on the amount of energy
will depend on the amount of energy ![]() which must be transferred to the system
in order to remove the electron to an infinitely great distance apart from the
nucleus. Denoting the charge of the electron and of the nucleus by -
which must be transferred to the system
in order to remove the electron to an infinitely great distance apart from the
nucleus. Denoting the charge of the electron and of the nucleus by -
![]() and
and ![]() respectively and the mass of the electron by
respectively and the mass of the electron by ![]() , we thus get
, we thus get
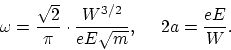 |
(1) |
Let us now, however, take the effect of the energy radiation into account,
calculated in the ordinary way from the acceleration of the electron. In this
case the electron will no longer describe stationary orbits. ![]() will
continuously increase, and the electron will approach the nucleus describing
orbits of smaller and smaller dimensions, and with greater and greater
frequency; the electron on the average gaining in kinetic energy at the same
time as the whole system loses energy. This process will go on until the
dimensions of the orbit are the same order of magnitude as the dimensions of the
electron or those of the nucleus. A simple calculation shows that the energy
radiated out during the process considered will be enormously great compared
with that radiated out by ordinary molecular processes.
will
continuously increase, and the electron will approach the nucleus describing
orbits of smaller and smaller dimensions, and with greater and greater
frequency; the electron on the average gaining in kinetic energy at the same
time as the whole system loses energy. This process will go on until the
dimensions of the orbit are the same order of magnitude as the dimensions of the
electron or those of the nucleus. A simple calculation shows that the energy
radiated out during the process considered will be enormously great compared
with that radiated out by ordinary molecular processes.
It is obvious that the behaviour of such a system will be very different from that of an atomic system occurring in nature. In the first place, the actual atoms in their permanent state to have absolutely fixed dimensions and frequencies. Further, if we consider any process, the result seems always to be that after a certain amount of energy characteristic for the systems in question is radiated out, the system will again settle down in a stable state of equilibrium, in which the distance apart of the particles are of the same order of magnitude as before the process.
Now the essential point in Planck's theory of radiation is that the energy
radiation from an atomic system does not take place in the continuous way
assumed in the ordinary electrodynamics, but that it, on the contrary, takes
place in distinctly separated emissions, the amount of energy radiated out from
an atomic vibrator of frequency ![]() in a single emission being equal to
in a single emission being equal to ![]() , where
, where ![]() is an entire number, and
is an entire number, and ![]() is a universal
constant.5
is a universal
constant.5
Returning to the simple case of an electron and a positive nucleus considered above, let us assume that the electron at the beginning of the interaction with the nucleus was at a great distance apart from the nucleus, and had no sensible velocity relative to the latter. Let us further assume that the electron after interaction has taken place has settled down in a stationary orbit around the nucleus. We shall, for reasons referred to later, assume that the orbit in question is circular: this assumption will, however, make no alteration in the calculations for system containing only a single electron.
Let as now assume that, during the binding of the electron, a homogeneous
radiation is emitted of a frequency ![]() , equal to half the frequency of
revolution of the electron in its final orbit; then from Planck's theory, we
might expect that the amount of energy emitted by the process considered is
equal to
, equal to half the frequency of
revolution of the electron in its final orbit; then from Planck's theory, we
might expect that the amount of energy emitted by the process considered is
equal to ![]() , where
, where ![]() is Planck's constant an entire number. If we
assume that the radiation emitted is homogeneous, the second assumption
concerning the frequency of the radiation suggests itself, since the frequency
of revolution of the electron at the beginning of the emission is 0. The
question, however, of the rigorous validity of both assumptions, and also of the
application made of Planck's theory, will be more closely discussed in
is Planck's constant an entire number. If we
assume that the radiation emitted is homogeneous, the second assumption
concerning the frequency of the radiation suggests itself, since the frequency
of revolution of the electron at the beginning of the emission is 0. The
question, however, of the rigorous validity of both assumptions, and also of the
application made of Planck's theory, will be more closely discussed in ![]() .
.
Putting
| (2) |
| (3) |
If in these expressions we give ![]() different values, we get a series of
values for
different values, we get a series of
values for ![]() ,
, ![]() , and
, and ![]() corresponding to a series of configurations of
the system. According to the above considerations, we are led to assume that
these configurations will correspond to states of the system in which there is
no radiation of energy; states which consequently will be stationary as long as
the system is not disturbed from outside. We see that the value of
corresponding to a series of configurations of
the system. According to the above considerations, we are led to assume that
these configurations will correspond to states of the system in which there is
no radiation of energy; states which consequently will be stationary as long as
the system is not disturbed from outside. We see that the value of ![]() is
greatest if
is
greatest if ![]() has its smallest value 1. This case will therefore correspond
to the most stable of the system, i.e., will correspond to the binding of the
electron for the breaking up of which the greatest amount of energy is required.
has its smallest value 1. This case will therefore correspond
to the most stable of the system, i.e., will correspond to the binding of the
electron for the breaking up of which the greatest amount of energy is required.
Putting in the above expressions ![]() and
and ![]() , and introducing the
experimental values
, and introducing the
experimental values
we get
We see that these values are of the same order of magnitude as the linear dimensions of the atoms, the optical frequencies, and the ionization- potentials.
The general importance of Planck's theory for the discussion of the behaviour of atomic system was originally pointed out by Einstein.6The considerations of Einstein have been developed and applied on a number of different phenomena, especially by Stark, Nernst, and Sommerfield. The agreement as to the order of magnitude between values observed for the frequencies and dimensions of the atoms, and values for these quantities calculated by considerations similar to those given above, has been the subject of much discussion. It was first pointed out by Haas,7 in ann attempt to explain the meaning and the value of Planck's constant on the basis of J.J. Thomson's atom-model, by help of the linear dimensions and frequency of an hydrogen atom. Systems of the kind considered in this paper, in which the forces between the particles vary inversely as the square of the distance, are discussed in relation to Planck's theory by J.W. Nicholson.8 In a series of papers this author has shown that it seems to be possible to account for lines of hitherto unknown origin in the spectra of the stellar nebulae and that of the solar corona, by assuming the presence in these bodies of certain hypothetical elements of exactly indicated constitution. The atoms of these elements are supposed to consist simply of a ring of a few electrons surrounding a positive nucleus of negligibly small dimensions. The ratios between the frequencies corresponding to the lines in question are compared with the ratios between the frequencies corresponding to different modes of vibration of the ring of electrons. Nicholson has obtained a relation to Planck's theory showing that the ratios between the wave-lenth of different sets of lines of the coronal spectrum can be accounted for with great accuracy by assuming that the ratio between the energy of the system and the frequency of rotation of the ring is equal to an entire multiple of Planck's constant. The quantity Nicholson refers to as the energy is equal to twice the quantity which we have denoted above by W. In the latest paper cited Nicholson has found it necessary to give the theory a more complicated form, still, however, representing the ratio of energy to frequency by a simple function of whole numbers.
The excellent agreement between the calculated and observed values of the ratios between the wave-length in question seems a strong argument in favour of the validity of the foundation of Nicholson's calculations. Serious objections, however, may be raised against the theory. These objections are intimately connected with the problem of the homogeneity of the radiation emitted. In Nicholson's calculations the frequency of lines in a line-spectrum is identified with the frequency of vibration of a mechanical system in a distinctly indicated state of equilibrium. As a relation from Planck's theory is used, we might expect that the radiation is sent out in quanta; but systems like those considered, in which the frequency is a function of the energy, cannot emit a finite amount of a homogeneous radiation; for, as soon as the emission of radiation is started, the energy and also the frequency of the system are altered. Further, according to the calculation of Nicholson, the systems are unstable for some modes of vibration. Apart from such objections - which may be only formal (see p. 23)?????? - it must be remarked, that the theory in the form given dies not seem to be able to account for the well-known laws of Balmer and Rydberg connecting the frequencies of the lines in the line- spectra of the ordinary elements.
It will now be attempted to show that the difficulties in question disappear if we consider the problems from the point of view taken in this paper. Before proceeding it may be useful to restate briefly the ideas characterizing the calculations on p. 5. The principal assumptions used are:
- (1)
- That the dynamical equilibrium of the systems in the stationary states can be discussed by help of the ordinary mechanics, while the passing of the systems between different stationary states cannot be treated on that basis.
- (2)
- That the latter is followed by the emission of a homogeneous radiation, for which the relation between the frequency and the amount of energy emitted is the one given by Planck's theory.
In the calculations on page 5 we have further made use of the more special
assumptions, viz., that the different stationary states correspond to the
emission of a different number of Planck's energy-quanta, and that the
frequency of the radiation emitted during the passing of the system from a state
in which no energy is yet radiated out to one of the stationary states, is equal
to half the frequency of revolution of the electron in the latter state. We can,
however (see ![]() ), also arrive at the expressions (3) for the stationary
states by using assumptions of somewhat different from. We shall, therefore,
postpone the discussion of the spacial assumptions, and first show how by the
help of the above principal assumptions, and of the expressions (3) for the
stationary states, we can account for the line-spectrum
of hydrogen.
), also arrive at the expressions (3) for the stationary
states by using assumptions of somewhat different from. We shall, therefore,
postpone the discussion of the spacial assumptions, and first show how by the
help of the above principal assumptions, and of the expressions (3) for the
stationary states, we can account for the line-spectrum
of hydrogen.
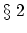 .Emission of Line-spectra
.Emission of Line-spectra
Spectrum of Hydrogen. - General evidence indicates that an atom of
hydrogen consist simply of a single electron rotating round a positive nucleus
of charge ![]() .9
The reformation of
a hydrogen atom, when the electron has been removed to great distances away
from the nucleus - e.g. by the effect of electrical discharge in a vacuum tube
- will accordingly correspond to the binding of an electron by a positive
nucleus considered on p. 5. If in (3) we put
.9
The reformation of
a hydrogen atom, when the electron has been removed to great distances away
from the nucleus - e.g. by the effect of electrical discharge in a vacuum tube
- will accordingly correspond to the binding of an electron by a positive
nucleus considered on p. 5. If in (3) we put ![]() , we get for the total
amount of energy radiated out by the formation of one of the stationary states,
, we get for the total
amount of energy radiated out by the formation of one of the stationary states,
The amount of energy emitted by the passing of the system from a state
corresponding to ![]() to one corresponding to
to one corresponding to ![]() , is
consequently
, is
consequently
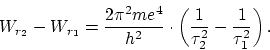
If now we suppose that the radiation is question is homogeneous, and that the amount of energy emitted is equal to
and from this
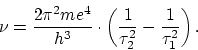 |
(4) |
We see that this expression accounts for the law connecting the lines in the
spectrum of hydrogen. If we put ![]() and let
and let ![]() vary, we get the
ordinary Balmer series. If we put
vary, we get the
ordinary Balmer series. If we put ![]() , we get the series in the
ultra-red observed by
Paschen10and previously suspected by Ritz. If we put
, we get the series in the
ultra-red observed by
Paschen10and previously suspected by Ritz. If we put ![]() and
and
![]() we get series respectively in the extreme ultraviolet and the extreme
ultra-red, which are not observed, but the existence of which may be
expected.
we get series respectively in the extreme ultraviolet and the extreme
ultra-red, which are not observed, but the existence of which may be
expected.
The agreement in question is quantitative as well as qualitative. Putting
we get
The observed value for the factor outside the bracket in the formula (4) is
We agreement between the theoretical and observed values is inside the uncertainty due to experimental errors in the constants entering in the expression for the theoretical value. We shall in
It may be remarked that the fact, that it has not been possibly to observe more
than 12 lines of the Balmer series in experiments with vacuum tubes, while 33
lines are observed in the spectra of some celestial bodies, is just what we
should expect from the above theory. According to the equation (3) the diameter
of the orbit of the electron in the different stationary states is proportional
to ![]() . For
. For ![]() the diameter is equal to
the diameter is equal to
![]() cm, or
equal to mean distance between the molecules in a gas at a pressure of about 7
mm mercury; for
cm, or
equal to mean distance between the molecules in a gas at a pressure of about 7
mm mercury; for ![]() the diameter is equal to
the diameter is equal to
![]() cm,
corresponding to the mean distance of the molecules at a pressure of about 0.02
mm mercury. According to the theory the necessary condition for the appearance
of a great number of lines is therefore a very small density of the gas; for
simultaneously to obtain an intensity sufficient for observation the space
filled with the gas must be very great. If the theory is right, we may
therefore never expect to be able in experiments with vacuum tubes to observe
the lines corresponding to high numbers of the Balmer series of the emission
spectrum of hydrogen; it might, however, be possible to observe the lines by
investigation of the absorption spectrum of this gas. (see
cm,
corresponding to the mean distance of the molecules at a pressure of about 0.02
mm mercury. According to the theory the necessary condition for the appearance
of a great number of lines is therefore a very small density of the gas; for
simultaneously to obtain an intensity sufficient for observation the space
filled with the gas must be very great. If the theory is right, we may
therefore never expect to be able in experiments with vacuum tubes to observe
the lines corresponding to high numbers of the Balmer series of the emission
spectrum of hydrogen; it might, however, be possible to observe the lines by
investigation of the absorption spectrum of this gas. (see ![]() ).
).
It will be observed that we in the above way do not obtain other series of
lines, generally ascribed to hydrogen; for instance, the series first observed
by Pickering11 in the spectrum of the star ![]() Puppis, and the set of series
recently found by Fowler12 by experiments with vacuum tubes containing a mixture of hydrogen
and helium. We shall, however, see that, by help of the above theory, we can
account naturally for these series of lines if we ascribe them to helium.
Puppis, and the set of series
recently found by Fowler12 by experiments with vacuum tubes containing a mixture of hydrogen
and helium. We shall, however, see that, by help of the above theory, we can
account naturally for these series of lines if we ascribe them to helium.
A neutral atom of the latter element consists, according to Rutherford's theory,
of a positive nucleus of charge ![]() and two electrons. Now considering the
binding of a single electron by a helium nucleus, we get putting
and two electrons. Now considering the
binding of a single electron by a helium nucleus, we get putting ![]() in the
expressions (3) on page 5, and proceeding in in exactly the same way as above,
in the
expressions (3) on page 5, and proceeding in in exactly the same way as above,
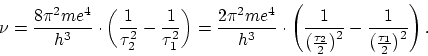
If we in this formula put
The reason why the spectrum considered is not observed in ordinary helium tubes may be that in such tubes the ionization of helium is not so complete in the star considered or in the experiments of Fowler, where a strong discharge was sent through a mixture of hydrogen and helium. The condition for the appearance of the spectrum is, according to the above theory, that helium atoms are present in a state in which they have lost both their electrons. Now we must assume that the amount of energy to be used in removing the second electron from a helium atom is much greater than that to be used in removing the first. Further, it is known from experiments on positive rays, that hydrogen atoms can acquire a negative charge; therefore the presence of hydrogen in the experiments of Fowler may effect that more electrons are removed from some of the helium atoms than would be the case if only helium were present.
Spectra of other substances. -- in case of systems containing more
electrons we must - in conformity with the result of experiments - expect more
complicated laws for the line-spectra than those considered. I shall try to show
that the point of view taken above allows, at any rate, a certain understanding
of the laws observed.
According to Rydberg's theory -- with the generalization given by
Ritz13 - the frequency
corresponding to the lines of the spectrum of an element can be expressed by
where
The circumstance that the frequency can be written as a difference between two
functions of entire numbers suggests an origin of the lines in the spectra in
question similar to the one we have assumed for hydrogen; i.e. that the lines
correspond to a radiation emitted during the passing of the system between two
different stationary states. For system containing more than one electron the
detailed discussion may be very complicated, as there will be many different
configurations of the electrons which can be taken into consideration as
stationary states. This may account for the difference sets of series in the
line spectra emitted from the substances in question. Here I shall only try to
show how, by help of the theory, it can be simple explained that the constant ![]() entering in Rydberg's formula is the same for all substances.
Let us assume that the spectrum in question corresponds to the radiation emitted
during the binding of an electron; and let us further assume that the system
including the electron considered is neutral. The force on the electron, when at
a great distance apart the nucleus and the electrons previously bound, will be
very nearly the same as the above case of the binding of an electron by a
hydrogen nucleus.
The energy corresponding to one of the stationary states will therefore for
entering in Rydberg's formula is the same for all substances.
Let us assume that the spectrum in question corresponds to the radiation emitted
during the binding of an electron; and let us further assume that the system
including the electron considered is neutral. The force on the electron, when at
a great distance apart the nucleus and the electrons previously bound, will be
very nearly the same as the above case of the binding of an electron by a
hydrogen nucleus.
The energy corresponding to one of the stationary states will therefore for
![]() great be very nearly equal to
that given by the expression (3) on p. 5, if
we put
great be very nearly equal to
that given by the expression (3) on p. 5, if
we put ![]() . For
. For ![]() great we consequently get
great we consequently get
in conformity with Rydberg's theory.
 .General Considerations Continued
.General Considerations Continued
We shall now return to the discussion (see p. 7) of the special assumptions used in deducing the expression (3) on p. 5 for the stationary states of a system consisting of an electron rotating round a nucleus.
For one, we have assumed that the different stationary states correspond to an emission of a different number of energy-qyanta. Considering systems in which the frequency is a function of the energy, this assumption, however, may be regarded as improbable; for as soon as one quantum in sent out the frequency is altered. We shall now see that we can leave the assumption used and still retain the equation (2) on p. 5, and thereby the formal analogy with Planck's theory.
Firstly, it will be observed that it has not been necessary, in order to account
for the law of the spectra by help of the expressions (3) for the stationary
states, to assume that in any case a radiation is sent out corresponding to more
than a single energy-quantum, ![]() . Further information on the
frequency of the radiation may be obtained by comparing calculations of the
energy radiation in the region of slow vibrations based on the above assumptions
with calculations based on the ordinary mechanics. As is known, calculations on
the latter basis are in agreement with experiments on the energy radiation in
the named region.
. Further information on the
frequency of the radiation may be obtained by comparing calculations of the
energy radiation in the region of slow vibrations based on the above assumptions
with calculations based on the ordinary mechanics. As is known, calculations on
the latter basis are in agreement with experiments on the energy radiation in
the named region.
Let us assume that the ratio between the total amount of energy emitted and the
frequency of revolution of the electron for the different stationary states is
given by the equation
![]() ,
instead of by the equation
(2). Proceeding in the same way as above, we get in this case instead of (3)
,
instead of by the equation
(2). Proceeding in the same way as above, we get in this case instead of (3)
Assuming as above that the amount of energy emitted during the passing of the
system from a state corresponding to ![]() to one for which
to one for which
![]() is equal to
is equal to ![]() , we get instead of (4)
, we get instead of (4)
We see that in order to get an expression of the same form as the Balmer series we must put
In order to determine ![]() let us now consider the passing of the system between
two successive stationary states corresponding to
let us now consider the passing of the system between
two successive stationary states corresponding to ![]() and
and ![]() ;
introducing
;
introducing
![]() , we get for the frequency of the radiation emitted
, we get for the frequency of the radiation emitted
For the frequency of revolution of the electron before and after the emission we
have
If ![]() is great the ratio between the frequency before and after the emission
will be very near equal to 1; and according to the ordinary electrodynamics we
should therefore expect that the ratio between the frequency of radiation and
the frequency of revolution also very nearly equal to 1. This condition will
only be satisfied if
is great the ratio between the frequency before and after the emission
will be very near equal to 1; and according to the ordinary electrodynamics we
should therefore expect that the ratio between the frequency of radiation and
the frequency of revolution also very nearly equal to 1. This condition will
only be satisfied if ![]() . Putting
. Putting
![]() , we,
however, again arrive at the equation (2) and consequently at the expression
(3) for the stationary states.
, we,
however, again arrive at the equation (2) and consequently at the expression
(3) for the stationary states.
If we consider the passing of the system between two states corresponding to
![]() and
and ![]() , where
, where ![]() is small compared with
is small compared with ![]() , we get with
the same approximation as above, putting
, we get with
the same approximation as above, putting
![]() ,
,
The possibility of an emission of a radiation of such a frequency may also be interpreted from analogy with the ordinary electrodynamics, as an electron rotating round a nucleus in an elliptical orbit will emit a radiation which according to Fourier's theorem can be resolved into homogeneous components, the frequency of which are
We are thus led to assume that the interpretation of the equation (2) is not
that the different stationary states correspond to an emission of different
numbers of energy-quanta, but that the frequency of the energy emitted
during the passing of the system from a state in which no energy is yet radiated
out to one of the different stationary states, is equal to different multiples
of ![]() , where
, where ![]() is the frequency of revolution of the
electron in the state considered. From this assumption we get exactly the same
expressions as before for the stationary states, and from these by help of the
principal assumptions on p. 7 the same expression for the law of the hydrogen
spectrum. Consequently we may regard our preliminary considerations on p. 5 only
as a simple from of representing the results of the theory.
is the frequency of revolution of the
electron in the state considered. From this assumption we get exactly the same
expressions as before for the stationary states, and from these by help of the
principal assumptions on p. 7 the same expression for the law of the hydrogen
spectrum. Consequently we may regard our preliminary considerations on p. 5 only
as a simple from of representing the results of the theory.
Before we leave the discussion of this question, we shall for a moment return to
the question of the significance of the agreement between the observed and
calculated values of the constant entering in the expressions (4) for the Balmer
series of the hydrogen spectrum. From the above consideration it will follow
that, taking the starting-point in the form of the law of the hydrogen
spectrum and assuming that the different lines correspond to a homogeneous
radiation emitted during the passing between different, stationary states, we
shall arrive at exactly the same expression for the constant in question as that
given by (4), if we only assume (1) that the radiation is sent out in quanta ![]() , and (2) that the frequency of the radiation emitted during the passing of
the system between successive stationary states will coincide with the frequency
of revolution of the electron in the region of slow vibrations.
, and (2) that the frequency of the radiation emitted during the passing of
the system between successive stationary states will coincide with the frequency
of revolution of the electron in the region of slow vibrations.
As all the assumptions used in this latter way of representing the theory are of
what we may call a qualitative character, we are justified in expecting -- if
the whole way of considering is a sound one - an absolute agreement between the
values calculated and observed for the constant in question, and not only an
approximate agreement. The formula (40 may therefore be of value in the
discussion of the results of experimental determinations of the constants ![]() ,
, ![]() , and
, and ![]() .
.
While there obviously can be no question of a mechanical foundation of the
calculations given in this paper, it is, however, possible to give a very simple
interpretation of the result of the calculation on p. 5 by help of symbols
taken from the ordinary mechanics. Denoting the angular momentum of the electron
round the nucleus by ![]() , we have immediately for a circular orbit
, we have immediately for a circular orbit
![]() , where
, where ![]() is the frequency of revolution and
is the frequency of revolution and ![]() the kinetic energy of the electron; for a circular orbit we further have
the kinetic energy of the electron; for a circular orbit we further have ![]() (see p. 3) and from (2), p. 5, we consequently get
(see p. 3) and from (2), p. 5, we consequently get
where
If we therefore assume that the orbit of the electron in the stationary states is circular, the result of the calculation on p. 5 can be expressed by the simple condition: that the angular momentum of the electron round the nucleus in a stationary state of the system is equal to an entire multiple of a universal value, independent of the charge on the nucleus. The possible importance of the angular momentum in the discussion of atomic systems in relation to Planck's theory is emphasized by Nicholson.14
The great number of different stationary states we do not observe expect by
investigation of the emission and absorption of radiation. It most of the other
physical phenomena, however, we only observe the atoms of the matter in a single
distinct state, i,e., the state of the atoms at low temperature. From the
preceding considerations we are immediately led to the assumption that the ``
permanent'' state is the one among the stationary states during the formation of
which the greatest amount of energy is emitted. According to the equation (3) on
p. 5, this state is the one which corresponds to ![]() .
.
 . Absorption of Radiation
. Absorption of Radiation
In order to account for Kirchhoff's law it is necessary to introduce assumptions
on the mechanism of absorption of radiation which correspond to those we have
used considering the emission. Thus we must assume that a system consisting of a
nucleus and an electron rotating round it under certain circumstances can
absorb a radiation of a frequency equal to the frequency of the homogenous
radiation emitted during the passing of the system between different stationary
states. Let us consider the radiation emitted during the passing of the system
between two stationary states ![]() and
and ![]() corresponding to values for
corresponding to values for ![]() equal to
equal to ![]() and
and
![]() . As the necessary condition of
the radiation in question was the presence of systems in the state
. As the necessary condition of
the radiation in question was the presence of systems in the state ![]() , we
must assume that the necessary condition for an absorption of the radiation is
the presence of systems in the state
, we
must assume that the necessary condition for an absorption of the radiation is
the presence of systems in the state ![]() .
.
These considerations seems to be in conformity with experiments on absorption in
gases. In hydrogen gas at ordinary conditions for instance there is no
absorption of a radiation of a frequency corresponding to the
line-spectrum of this gas; such an absorption is only observed in
hydrogen gas in a luminous state. This is what we should expect according to the
above. We have on p. 9 assumed that the radiation in question was emitted during
the passing of the systems between stationary states corresponding to ![]() . The state of the atoms in hydrogen gas at ordinary conditions should,
however, correspond to
. The state of the atoms in hydrogen gas at ordinary conditions should,
however, correspond to ![]() ; furthermore, hydrogen atoms at ordinary
conditions combine into molecules, i.e., into system in which the electrons have
frequencies different from those in the atoms (see Part III.) From the
circumstance that certain substances in a non-lumimous state, as, foe
instance, sodium vapour, absorb radiation corresponding to lines in the
line-spectra of the substances, we may, on the other hand, conclude that the
lines in question are emitted during the passing of the system between two
states, one of which is the permanent state.
; furthermore, hydrogen atoms at ordinary
conditions combine into molecules, i.e., into system in which the electrons have
frequencies different from those in the atoms (see Part III.) From the
circumstance that certain substances in a non-lumimous state, as, foe
instance, sodium vapour, absorb radiation corresponding to lines in the
line-spectra of the substances, we may, on the other hand, conclude that the
lines in question are emitted during the passing of the system between two
states, one of which is the permanent state.
How much the above considerations differ from an interpretation based on the
ordinary electrodynamic of perhaps most early shown by the fact that we have
been forced to assume that a system of electrons will absorb a radiation of a
frequency different from the frequency of vibration of the electrons calculated
in the ordinary way. It may in this connexion be of interest to mention a
generalization of the considerations to which we are led by experiments on the
photo-electric effect and which may be able to throw some light on the
problem in question. Let us consider state of the system in which the electron
is free, i.e., in which the electron possesses kinetic energy sufficient to
remove to infinite distances from the nucleus. If we assume that the motion of
the electron is governed by the ordinary mechanics and that there is no (
sensible) energy radiation, the total energy of the system - as in the above
considered stationary states - will be constant. Further, there will be perfect
continuity between the two kinds of states, as the difference between frequency
and dimensions of the system in successive stationary states will diminish
without limit if ![]() increases. In the following considerations we shall for
the sake of brevity refer to the two kinds of states in question as ``
mechanical'' states; by this notation only emphasizing the assumption that the
motion of the electron in both cases can be assumed for by the ordinary
mechanics.
increases. In the following considerations we shall for
the sake of brevity refer to the two kinds of states in question as ``
mechanical'' states; by this notation only emphasizing the assumption that the
motion of the electron in both cases can be assumed for by the ordinary
mechanics.
Tracing the analogy between the two kinds of mechanical states, we might now
expect the possibility of an absorption of radiation, not only corresponding to
the passing of the system between two different stationary states, but also
corresponding to the passing between one of the stationary states and a state in
which the electron is free; and as above, we might expect that the frequency of
this radiation was determined by the equation ![]() , where
, where ![]() is the
difference between the total energy of the system in the two states. As it will
be see, such an absorption of radiation is just what is observed in experiments
on ionization by ultra-violet light and by Röntgen rays. Obviously, we
get in this way the same expression for the kinetic energy of an electron
ejected from an atom by photo-electron effect as that deduced by
Einstein15i.e.,
is the
difference between the total energy of the system in the two states. As it will
be see, such an absorption of radiation is just what is observed in experiments
on ionization by ultra-violet light and by Röntgen rays. Obviously, we
get in this way the same expression for the kinetic energy of an electron
ejected from an atom by photo-electron effect as that deduced by
Einstein15i.e., ![]() , where
, where ![]() is the kinetic energy of the electron ejected,
and
is the kinetic energy of the electron ejected,
and ![]() the total amount of energy emitted during the original binding of the
electron.
the total amount of energy emitted during the original binding of the
electron.
The above considerations may further account for the result of some experiments
of R.W. Wood16 on absorption
of light by sodium vapour. In these experiments, an absorption corresponding to
a very great number of lines in the principal series of the sodium spectrum is
observed, and in addition a continuous absorption which begins at the head of
the series and extends to the extreme ultra-violet. This is exactly what
we should expect according to the analogy in question, and, as we shall see, a
closer consideration of the above experiments allows us to trance the analogy
still further. As mentioned on p. 9 the radii of the orbits of the electrons
will for stationary states, corresponding to high values for ![]() be very
great compared with ordinary atomic dimensions. This circumstance was used as an
explanation of the non-appearance in experiments with vacuum-tubes
of lines corresponding to the higher numbers in the Balmer series of the
hydrogen spectrum. This is also in conformity with experiments on the emission
spectrum of sodium; in the principal series of the emission spectrum of this
substance rather few lines are observed. Now in Wood's experiments the pressure
was not very low, the states corresponding to high values for
be very
great compared with ordinary atomic dimensions. This circumstance was used as an
explanation of the non-appearance in experiments with vacuum-tubes
of lines corresponding to the higher numbers in the Balmer series of the
hydrogen spectrum. This is also in conformity with experiments on the emission
spectrum of sodium; in the principal series of the emission spectrum of this
substance rather few lines are observed. Now in Wood's experiments the pressure
was not very low, the states corresponding to high values for ![]() could
therefore not appear; yet in the absorption spectrum about 50 lines were
detected. In the experiments in question we consequently observe an absorption
of radiation which is not accompanied by a complete transition between two
different stationary states. According to the present theory we must assume that
this absorption is followed by an emission of energy during which the systems
pass back to the original stationary state. If there are no collisions between
the different systems this energy will be emitted as a radiation of the same
frequency as that absorbed, and there will be no true absorption but only a
scattering of the original radiation; a true absorption will not occur unless
the energy in question is transformed by collisions into kinetic energy of free
particles. In analogy we may now from the above experiments conclude that a
bound electron - also in cases in which three is no ionization - will have an
absorbing (scattering) influence on a homogeneous radiation, as soon as the
frequency of the radiation is greater than
could
therefore not appear; yet in the absorption spectrum about 50 lines were
detected. In the experiments in question we consequently observe an absorption
of radiation which is not accompanied by a complete transition between two
different stationary states. According to the present theory we must assume that
this absorption is followed by an emission of energy during which the systems
pass back to the original stationary state. If there are no collisions between
the different systems this energy will be emitted as a radiation of the same
frequency as that absorbed, and there will be no true absorption but only a
scattering of the original radiation; a true absorption will not occur unless
the energy in question is transformed by collisions into kinetic energy of free
particles. In analogy we may now from the above experiments conclude that a
bound electron - also in cases in which three is no ionization - will have an
absorbing (scattering) influence on a homogeneous radiation, as soon as the
frequency of the radiation is greater than ![]() , where
, where ![]() is the total amount
of energy emitted during the binding of the electron. This would be highly in
favour of a theory of absorption as the one sketched above, as there can in such
a case be no question of a coincidence of the frequency of the radiation and a
characteristic frequency of vibration of the electron. If will further be seen
that the assumption, that there will be an absorption (scattering) of any
radiation corresponding to a transition between two different mechanical states,
is in perfect analogy with the assumption generally used that a free electron
will have an absorbing (scattering) influence on light of any frequency.
Corresponding considerations will hold for the emission of radiation.
is the total amount
of energy emitted during the binding of the electron. This would be highly in
favour of a theory of absorption as the one sketched above, as there can in such
a case be no question of a coincidence of the frequency of the radiation and a
characteristic frequency of vibration of the electron. If will further be seen
that the assumption, that there will be an absorption (scattering) of any
radiation corresponding to a transition between two different mechanical states,
is in perfect analogy with the assumption generally used that a free electron
will have an absorbing (scattering) influence on light of any frequency.
Corresponding considerations will hold for the emission of radiation.
In analogy to the assumption used in this paper that the emission of line- spectra is due to the re-formation of atoms after one or more of the lightly bound electrons are removed, we may assume that the homogeneous Röntgen radiation is emitted during the setting down of the systems after one of the firmly bound electrons escapes, e.g. by impact of cathode particles.17 In the next part in this paper, dealing with the constitution of atoms, we shall consider the question more closely and try to show that a calculation based on this assumption is in quantitative agreement with the results of experiments: here we shall only mention briefly a problem with which we meet in such a calculation.
Experiments on the phenomena of X-rays suggest that not only the emission
and absorption of radiation cannot be treated by the help of the ordinary
electrodynamics, but not even the result of a collision between two electrons of
which the one is bound in an atom. This is perhaps most early shown by some very
instructive calculations on the energy of ![]() -particles emitted from
radioactive substances recently published by Rutherford.18
These calculations strongly suggest that
an electron of great velocity in passing through an atom and colliding with the
electrons bound will loose energy in distinct finite quanta. As is immediately
seen, this is very different from what we might expect if the result of the
collisions was governed by the usual mechanical laws. The failure of the
classical mechanics in such a problem might also be expected beforehand from the
absence of anything like equipartition of kinetic energy between free electrons
and electrons bound in atoms. From the point of view of the ``mechanical''
states we see, however, that the following assumption - which is in accord with
the above analogy - might be able to account for the result of Rutherford's
calculation and for the absence of equipartition of kinetic energy; two
colliding electrons, bound or free, will, after the collision as well as before,
be in mechanical states. Obviously, the introduction of such an assumption would
not make any alteration necessary in the classical treatment of a collision
between two free particles. But, considering a collision between a free and a
bound electron, it would follow that the bound electron by the collision could
not acquire a less amount of energy than the difference in energy corresponding
to successive stationary states, and consequently that the free electron which
collides with it could not lose a less amount.
-particles emitted from
radioactive substances recently published by Rutherford.18
These calculations strongly suggest that
an electron of great velocity in passing through an atom and colliding with the
electrons bound will loose energy in distinct finite quanta. As is immediately
seen, this is very different from what we might expect if the result of the
collisions was governed by the usual mechanical laws. The failure of the
classical mechanics in such a problem might also be expected beforehand from the
absence of anything like equipartition of kinetic energy between free electrons
and electrons bound in atoms. From the point of view of the ``mechanical''
states we see, however, that the following assumption - which is in accord with
the above analogy - might be able to account for the result of Rutherford's
calculation and for the absence of equipartition of kinetic energy; two
colliding electrons, bound or free, will, after the collision as well as before,
be in mechanical states. Obviously, the introduction of such an assumption would
not make any alteration necessary in the classical treatment of a collision
between two free particles. But, considering a collision between a free and a
bound electron, it would follow that the bound electron by the collision could
not acquire a less amount of energy than the difference in energy corresponding
to successive stationary states, and consequently that the free electron which
collides with it could not lose a less amount.
The preliminary and hypothetical character of the above considerations needs not to be emphasized. The intention, however, has been to show that the sketched generalization of the theory of the stationary states possibly may afford a simple basis of representing a number of experimental facts which cannot be explained by help of the ordinary electrodynamics, and that assumptions used do not seem to be inconsistent with experiments on phenomena for which a satisfactory explanation has been given by the classical dynamics and the wave theory of light.
 .The permanent State of an Atomic System
.The permanent State of an Atomic System
We shall now return to the main object of this paper - the discussion of the
``permanent'' state of a system consisting of nuclei and bound electrons. For a
system consisting of a nucleus and an electron rotating round it, this state is,
according to the above, determined by the condition that the angular momentum of
the electron round the nucleus is equal to ![]() .
.
On the theory of this paper the only neutral atom which contains a single
electron is the hydrogen atom. The permanent state of this atom should
correspond to the values of ![]() and
and ![]() calculated on p. 5. Unfortunately,
however, we know very little of the behaviour of hydrogen atoms on account of
the small dissociation of hydrogen molecules at ordinary temperatures. In order
to get a closer comparison with experiments, it is necessary to consider more
complicated systems.
calculated on p. 5. Unfortunately,
however, we know very little of the behaviour of hydrogen atoms on account of
the small dissociation of hydrogen molecules at ordinary temperatures. In order
to get a closer comparison with experiments, it is necessary to consider more
complicated systems.
Considering systems in which more electrons are bound by a positive nucleus, a configuration of the electrons which presents itself as a permanent state is in which the electrons are arranged in a ring round the nucleus. In the discussion of this problem on the basis of the ordinary electrodynamics, we meet- apart from the question of the energy radiation - with new difficulties due to the question of the stability of the ring. Disregarding for a moment this latter difficulty, we shall first consider the dimensions and frequency of the systems in relation to Planck's theory of radiation.
Let us consider a ring consisting of ![]() electrons rotating round a nucleus of
charge
electrons rotating round a nucleus of
charge ![]() , the electrons being arranged at equal angular intervals the
circumference of a circle of radius
, the electrons being arranged at equal angular intervals the
circumference of a circle of radius ![]() .
.
The total potential energy of the system consisting of the electrons and the
nucleus is
where
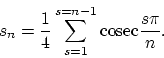
For the radial force exerted on an electron by the nucleus and the other electrons we get
Denoting the kinetic energy of an electron by ![]() and neglecting the
electromagnetic forces due to the motion of the electrons (see Part II), we get,
putting the centrifugal force on an electron equal to the radial force,
and neglecting the
electromagnetic forces due to the motion of the electrons (see Part II), we get,
putting the centrifugal force on an electron equal to the radial force,
or
>From this we get for the frequency of revolution
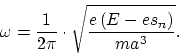
The total amount of energy
equal to the total kinetic energy of the electrons.
We see that the only difference in the above formula and those holding for the
motion of a single electron in a circular orbit round a nucleus is the exchange
of ![]() for
for ![]() . It is also immediately seen that corresponding to the
motion of an electron in an elliptical orbit round a nucleus, there will be a
motion of the
. It is also immediately seen that corresponding to the
motion of an electron in an elliptical orbit round a nucleus, there will be a
motion of the ![]() electrons in which each rotates in an elliptical orbit with
the nucleus in the focus, and the
electrons in which each rotates in an elliptical orbit with
the nucleus in the focus, and the ![]() electrons at any moment are situated at
equal angular intervals on a circle with the nucleus as the centre. The major
axis and frequency of the orbit of the single electrons will for this motion be
given by the expressions (1) on p. 3 if we replace
electrons at any moment are situated at
equal angular intervals on a circle with the nucleus as the centre. The major
axis and frequency of the orbit of the single electrons will for this motion be
given by the expressions (1) on p. 3 if we replace ![]() by
by ![]() and
and ![]() by
by
![]() . Let us now suppose that the system of
. Let us now suppose that the system of ![]() electrons rotating in a
ring round a nucleus is formed in a way analogous to the one assumed for a
single electron rotating round a nucleus. It will thus be assumed that the
electrons, before the binding by the nucleus, were at a great distance apart
from the latter and possessed no sensible velocities, and also that during the
binding a homogeneous radiation is emitted. As in the case of a single electron,
we have here that the total amount of energy emitted during the formation of the
system is equal to the final kinetic energy of the electrons. If we now suppose
that during the formation of the system the electrons at any moment are situated
at equal angular intervals on the circumference of a circle with the nucleus in
the centre, from analogy with the considerations, on p. 5 we are here led to
assume the existence of a series of stationary configurations in which the
kinetic energy per electron is equal to
electrons rotating in a
ring round a nucleus is formed in a way analogous to the one assumed for a
single electron rotating round a nucleus. It will thus be assumed that the
electrons, before the binding by the nucleus, were at a great distance apart
from the latter and possessed no sensible velocities, and also that during the
binding a homogeneous radiation is emitted. As in the case of a single electron,
we have here that the total amount of energy emitted during the formation of the
system is equal to the final kinetic energy of the electrons. If we now suppose
that during the formation of the system the electrons at any moment are situated
at equal angular intervals on the circumference of a circle with the nucleus in
the centre, from analogy with the considerations, on p. 5 we are here led to
assume the existence of a series of stationary configurations in which the
kinetic energy per electron is equal to
![]() , where
, where ![]() is an entire number,
is an entire number, ![]() Planck's constant, and
Planck's constant, and ![]() the frequency of
revolution. The configuration in which the greatest amount of energy is emitted
is, as before, the one in which
the frequency of
revolution. The configuration in which the greatest amount of energy is emitted
is, as before, the one in which ![]() . This configuration we shall assume
to be the permanent state of the system if the electrons in this state are
arranged in a single ring. As for the case of a single 3electron we get that the
angular momentum of each of the electrons is equal to
. This configuration we shall assume
to be the permanent state of the system if the electrons in this state are
arranged in a single ring. As for the case of a single 3electron we get that the
angular momentum of each of the electrons is equal to ![]() . It may
be remarked that instead of considering the single electrons we might have
considered the ring as an entity. This would, however, lead to the same result,
for in this case the frequency of revolution
. It may
be remarked that instead of considering the single electrons we might have
considered the ring as an entity. This would, however, lead to the same result,
for in this case the frequency of revolution ![]() will be replaced by the
frequency
will be replaced by the
frequency ![]() of the radiation from the whole ring calculated from
ordinary electrodynamics, and
of the radiation from the whole ring calculated from
ordinary electrodynamics, and ![]() by the total kinetic energy
by the total kinetic energy ![]() .
.
There may be many other stationary states corresponding to other ways of forming
the system. The assumption of the existence of such states seems necessary in
order to account for the line-spectra of systems containing more than one
electron (p. 11); it is also suggested by the theory of Nicholson mentioned on
p. 6, to which we shall return in a moment. The consideration of the spectra,
however, gives, as far as I can see, no indication of the existence of
stationary states in which all the electrons are arranged in a ring and which
correspond to greater values for the total energy emitted than the one we above
have assumed to be the permanent state.
Further, there may be stationary configurations of a system of ![]() electrons and
a nucleus of charge
electrons and
a nucleus of charge ![]() in which all the electrons are not arranged in a single
ring. The question, however, of the existence of such stationary configurations
is not essential for our determination of the permanent state, as long as we
assume that the electrons in this state of the system are arranged in a single
ring. Systems corresponding to more complicated configurations will be discussed
on p. 24.?????
in which all the electrons are not arranged in a single
ring. The question, however, of the existence of such stationary configurations
is not essential for our determination of the permanent state, as long as we
assume that the electrons in this state of the system are arranged in a single
ring. Systems corresponding to more complicated configurations will be discussed
on p. 24.?????
Using the relation
![]() we get, by help of the above
expressions for
we get, by help of the above
expressions for ![]() and
and ![]() , values for
, values for ![]() and
and ![]() corresponding to
the permanent state of the system which only differ from those given by the
equations (3) on p. 5, by exchange of
corresponding to
the permanent state of the system which only differ from those given by the
equations (3) on p. 5, by exchange of ![]() for
for ![]() .
.
The question of stability of a ring of electrons rotating round a positive charge is discussed in great detail by Sir. J.J. Thomson19 An adaption of Thomson's analysis for the case here considered of a ring rotating round a nucleus of negligibly small linear dimensions is given by Nicholson.20 The investigation of the problem in question naturally divides in two parts: one concerning the stability for displacements of the electrons on the plane of the ring; one concerning displacements perpendicular to this plane. As Nicholson's calculations show, the answer to the question of stability differs very much in the two cases in question. While the ring for the latter displacements in general is stable if the number of electrons is not great; the ring is in no case considered by Nicholson stable for displacement of the first kind.
According, however, to the point of view taken in this paper, the question of stability for displacements of the electrons in the plane of the ring is most intimately connected with the question of the mechanism of the binding of the electrons, and like the latter cannot be treated on the basis of the ordinary dynamics. The hypothesis of which we shall make use in the following is that the stability of a ring of electrons rotating round a nucleus is secured through the above condition of the universal constancy of the angular momentum, together with the further condition that the configuration of the particles is the one by the formation of which the greatest of energy is emitted. As will be shown, this hypothesis is, concerning the question of stability for a displacement of the electrons perpendicular to the plane of the ring, equivalent to that used in ordinary mechanical calculations.
Returning to the theory of Nicholson on the origin of lines observed in the spectrum of the solar corona, we shall now see that the difficulties mentioned on p. 7 may be only formal. In the first place, from the point of view considered above the objection as to the instability of the systems for displacements of the electrons in the plane of the ring may not be valid. Further, the objection as to emission of the radiation in quanta will not have reference to the calculations in question, if we assume that in the coronal spectrum we are not dealing with a true emission but only with a scattering of radiation. This assumption seems probable if we consider the conditions in the celestial body in question: for on account comparatively few collisions to disturb the stationary states and to cause a true emission of light corresponding to the transition between different stationary states; on the other hand there will in the solar corona be intense illumination of light of all frequencies which may excite the natural vibrations of the systems in the different stationary states. If the above assumption is correct, we immediately understand the entirely different from for the laws connecting the lines discussed by Nicholson and those connecting the ordinary line-spectra considered in this paper.
Proceeding to consider systems of more complicated constitution, we shall make use of the following theorem, which can be very simply proved; - ``In every system consisting of electrons and positive nuclei, in which the nuclei are at rest and the electrons move in circular orbits with a velocity small compared with the velocity of light, the kinetic energy will be numerically equal to half the principal energy.''
By help of this theorem we get - as in the previous cases of a single electron or of a ring rotating round a nucleus - that the total amount of energy emitted, by the formation of the systems from a configuration in which the distances apart of the particles are infinitely great and in which the particles have no velocities relative to each other, is equal to the kinetic energy of the electrons in the final configuration.
In analogy with the case of a single ring we are here led to assume that
corresponding to any configuration of equilibrium a series of geometrically
similar, stationary configuration of the system will exist in which the kinetic
energy of every electron is equal to the frequency of revolution multiplied by
![]() where
where ![]() is an entire number and
is an entire number and ![]() Planck's constant. In
any such series of stationary configurations the one corresponding to the
greatest amount of energy emitted will be the one in which
Planck's constant. In
any such series of stationary configurations the one corresponding to the
greatest amount of energy emitted will be the one in which ![]() for every
electron is equal to 1. Considering that the ratio of kinetic energy to
frequency for a particle rotating in a circular orbit is equal to
for every
electron is equal to 1. Considering that the ratio of kinetic energy to
frequency for a particle rotating in a circular orbit is equal to ![]() times
the angular momentum round the center of the orbit, we are therefore led to the
following simple generalization of the hypotheses mentioned on
pp. 15 and 22. ??????
times
the angular momentum round the center of the orbit, we are therefore led to the
following simple generalization of the hypotheses mentioned on
pp. 15 and 22. ??????
``In any molecular system consisting of positive nuclei and electrons in
which the nuclei are at rest relatire to each other and the electrons more in
circular orbits, the angular momentum of every electron round the centre of its
orbit will in the permanent state of the system be equal to ![]() ,
where
,
where ![]() is Planck's constant.''21
is Planck's constant.''21
In analogy with the considerations on p. 23, we shall assume that a configuration satisfying this condition is stable if the total energy of the system is less than in any neighbouring configuration satisfying the same condition of the angular momentum of the electrons.
As mentioned in the introduction, the above hypothesis will be used in a following communication as a basis for a theory of the constitution of atoms and molecules. It will be shown that it leads to results which seem to be in conformity with experiments on a number of different phenomena.
The foundation of the hypothesis has been sought entirely in its relation with Planck's theory of radiation; by help of considerations given later it will be attempted to throw some further light on the formation of it from another point of view.
Part II. - Systems containing only a Single Nucleus22
 General Assumptions
General Assumptions
Following the theory of Rutherford, we shall assume that the atoms of the elements consist of a positively charged nucleus surrounded by a cluster of electrons. The nucleus is the seat of the essential part of the mass of the atom, and has linear dimensions exceedingly small compared with the distance apart of the electrons in the surrounding cluster.
As in the previous paper, we shall assume that the cluster of electrons is
formed by the successive binding by the nucleus of electrons initially nearly at
rest, energy at the same time being radiated away. This will go on until, when
the total negative charge on the bound electrons is numerically equal to the
positive charge on the nucleus, the system will be neutral and no longer able to
exert sensible forces on electrons at distances from the nucleus great in
comparison with the dimensions of the orbits of the bound electrons. We may
regard the formation of helium from ![]() rays as an observed example of a
process of this kind, an
rays as an observed example of a
process of this kind, an ![]() particle on this view being identical with the
nucleus of a helium atom.
particle on this view being identical with the
nucleus of a helium atom.
On account of the small dimensions of the nucleus, its internal structure will not be of sensible influence on the constitution of the cluster of electrons, and consequently will have no effect on the ordinary physical and chemical properties of the atom. The latter properties on this theory will depend entirely on the total charge and mass of the nucleus; the internal structure of the nucleus will be of influence only on the phenomena of radioactivity.
>From the result of experiments on large-angle scattering of
![]() -rays, Rutherford23 found an electric charge on the nucleus corresponding per atom
to a number of electrons approximately equal to half the atomic weight. This
result seems to be in agreement with the number of electrons per atom calculated
from experiments on scattering of
Röntgen radiation.24 The total experimental evidence supports the
hypothesis25 that
the actual number of electrons in a neutral atom with a few exceptions is equal
to the number which indicated the position of the corresponding element in the
series of element arranged in order of increasing atomic weight. For example on
this view, the atom of oxygen which is the eighth element of the series has
eight electrons and a nucleus carrying eight unit charges.
-rays, Rutherford23 found an electric charge on the nucleus corresponding per atom
to a number of electrons approximately equal to half the atomic weight. This
result seems to be in agreement with the number of electrons per atom calculated
from experiments on scattering of
Röntgen radiation.24 The total experimental evidence supports the
hypothesis25 that
the actual number of electrons in a neutral atom with a few exceptions is equal
to the number which indicated the position of the corresponding element in the
series of element arranged in order of increasing atomic weight. For example on
this view, the atom of oxygen which is the eighth element of the series has
eight electrons and a nucleus carrying eight unit charges.
We shall assume that the electrons are arranged at equal angular intervals in
coaxial rings rotating round the nucleus. In order to determine the frequency
and dimensions of the rings we shall use the main hypothesis of the first paper,
viz.; that in the permanent state of an atom the angular momentum of every
electron round the centre of its orbit is equal to the universal value
![]() , where
, where ![]() is Planck's constant.
We shall take as a condition of stability, that the total energy of the system
in the configuration in question is less than in any neighbouring configuration
satisfying the same condition of the angular momentum of the electrons.
is Planck's constant.
We shall take as a condition of stability, that the total energy of the system
in the configuration in question is less than in any neighbouring configuration
satisfying the same condition of the angular momentum of the electrons.
If the charge on the nucleus and the number of electrons in the different rings
is known, the condition in regard to the angular momentum of the electrons will,
as shown in ![]() , completely determine the configuration of the system. i.e.,
the frequency of revolution and the linear dimensions of the rings.
Corresponding to different distributions of the electrons in the rings, however,
there will, in general, be more than one configuration which will satisfy the
condition of the angular momentum together with the condition of stability.
, completely determine the configuration of the system. i.e.,
the frequency of revolution and the linear dimensions of the rings.
Corresponding to different distributions of the electrons in the rings, however,
there will, in general, be more than one configuration which will satisfy the
condition of the angular momentum together with the condition of stability.
In ![]() and
and ![]() it will be shown that, on the general view of the formation
of the atoms, we are led to indications of the arrangement of the electrons in
the rings which are consistent with those suggested by the chemical properties
of the corresponding element.
it will be shown that, on the general view of the formation
of the atoms, we are led to indications of the arrangement of the electrons in
the rings which are consistent with those suggested by the chemical properties
of the corresponding element.
In ![]() will be shown that it is possible from the theory to calculate the
momentum velocity of cathode rays necessary to produce the characteristic
Röntgen radiation from the element, and that this is in approximate agreement
with the experimental values.
will be shown that it is possible from the theory to calculate the
momentum velocity of cathode rays necessary to produce the characteristic
Röntgen radiation from the element, and that this is in approximate agreement
with the experimental values.
In ![]() the phenomena of radioactivity will be briefly considered in relation
of the theory.
the phenomena of radioactivity will be briefly considered in relation
of the theory.
 Configuration and Stability of the System
Configuration and Stability of the System
Let us consider an electron of charge ![]() and mass
and mass ![]() which moves in a circular
orbit of radius
which moves in a circular
orbit of radius ![]() with a velocity
with a velocity ![]() small compared with the velocity of
light. Let us denote the radial force acting on the electrons by
small compared with the velocity of
light. Let us denote the radial force acting on the electrons by
![]() ;
; ![]() will in general be dependent on
will in general be dependent on ![]() . The condition of
dynamical equilibrium gives
. The condition of
dynamical equilibrium gives
Introducing the condition of universal constancy of the angular momentum of the
electron, we have
>From these two conditions we now get
| (5) |
| (6) |
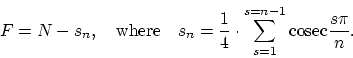
The values for
For systems consisting of nuclei and electrons in which the first are at rest
and the latter move in circular orbits with a velocity small compared with the
velocity of light, we have shown (see part I., p. 21)???? that the total kinetic
energy of the electrons is equal to the total amount of energy emitted during
the formation of the system from an original configuration in which all the
particles are at rest and at infinite distances from each other. Denoting this
amount of energy by ![]() , we consequently get
, we consequently get
| (7) |
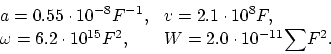 |
(8) |
In neglecting the magnetic forces due to the motion of the electrons we have in
Part I. assumed that the velocities of the particles are small compared with the
velocity of light. The above calculations show that for this to hold, ![]() must
be small compared with 150. As will be seen, the latter condition will be
satisfied for all the electrons in the atoms of elements of low atomic weight
and for a greater part of the electrons contained in the atoms of the other
elements.
must
be small compared with 150. As will be seen, the latter condition will be
satisfied for all the electrons in the atoms of elements of low atomic weight
and for a greater part of the electrons contained in the atoms of the other
elements.
If the velocity of the electrons in not small compared with the velocity of
light, the constancy of the angular momentum no longer involved a constant ratio
between the energy and the frequency of revolution. Without introducing new
assumptions, we cannot therefore in this case determine the configuration of the
systems on the basis of the consideration in Part I. Considerations given later
suggest, however, that the constancy of the angular momentum is the principal
condition. applying this condition for velocities not small compared with the
velocity of light, we get the same expression for ![]() as that given by (1),
while the quantity
as that given by (1),
while the quantity ![]() in the expressions for
in the expressions for ![]() and
and ![]() is replaced by
is replaced by
![]() ,
and in the expression for
,
and in the expression for ![]() by
by
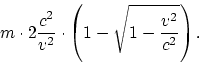
As stated in Part I., a calculation based on the ordinary mechanics given the result, that a ring of electrons rotating round a positive nucleus in general is unstable for displacement of the electrons in the plane of the ring. In order to escape from this difficulty, we have assumed that the ordinary principles of mechanics cannot be used in the discussion of the problem in question, any more than in the discussion of the connected problem of the mechanism of binding of electrons. We have also assumed that the stability for such displacement is secured through the introduction of the hypothesis of the universal constancy of the angular momentum of the electrons.
As is easily shown, the latter assumption in included in the condition of
stability in ![]() . Consider a ring of electrons rotation round a nucleus, and
assume that the system is in dynamical equilibrium and that the radius of the
ring is
. Consider a ring of electrons rotation round a nucleus, and
assume that the system is in dynamical equilibrium and that the radius of the
ring is ![]() , the
, the ![]() , the total kinetic energy
, the total kinetic energy ![]() , and the potential
energy
, and the potential
energy ![]() . As shown in Part i. (p. 21) we have
. As shown in Part i. (p. 21) we have ![]() . Next consider
a configuration of the system in which the electrons, under influence of
extraneous forces, rotate with the same angular momentum round the nucleus in a
ring of radius
. Next consider
a configuration of the system in which the electrons, under influence of
extraneous forces, rotate with the same angular momentum round the nucleus in a
ring of radius
![]() . In this case we have
. In this case we have
![]() , and on account of the uniformity of the angular momentum
, and on account of the uniformity of the angular momentum
![]() and
and
![]() .
Using the relation
.
Using the relation ![]() , we get
, we get
We see that the total energy of the new configuration is greater than in the original. according to the condition of stability in
In considering the stability of a ring of electrons rotating round a nucleus for
displacements of the electrons perpendicular to the plane of the ring, imagine a
configuration of the system in which the electrons are displaced by
![]() respectively, and suppose that the
electrons, under influence of extraneous forces, rotate in circular orbits
parallel to the original plane with the same radial and the same angular
momentum round the axis of the system as before. The kinetic energy is unaltered
by the displacement, and neglecting powers of the quantities
respectively, and suppose that the
electrons, under influence of extraneous forces, rotate in circular orbits
parallel to the original plane with the same radial and the same angular
momentum round the axis of the system as before. The kinetic energy is unaltered
by the displacement, and neglecting powers of the quantities
![]() higher than the second, the increase of the potential energy of the
system is given by
higher than the second, the increase of the potential energy of the
system is given by
where
| (9) |
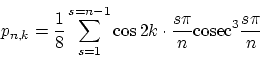
has its smallest value. This condition is identical with the condition of stability for displacements of the electrons perpendicular to the plane of the ring, deduced by help of ordinary mechanical considerations.26
A suggestive illustration is obtained by imagining that the displacements considered are produced by the effect of extraneous forces acting on the electrons in a direction parallel to the axis of the ring. If the displacements are produced infinitely slowly the motion of the electrons will at any moment be parallel to the original plane of the ring, and the angular momentum of each of the electrons round the centre of its orbit will obviously be equal to its original value; the increase in the potential energy of the system will be equal to the work done by the extraneous forces during the displacements we are led to assume that the ordinary mechanics can be used in calculating the vibrations of the electrons perpendicular to the plane of the ring - contrary to the ease of vibrations in the plane of the ring. This assumptions is supposed by the apparent agreement with observations obtained by Nicholson in his theory of the origin of lines in the spectra of the solar corona and stellar nebulae (see Part I. pp. 6 & 23).?????? In addition it will be shown later that the assumption seems to be in agreement with experiments on dispersion.
The following table gives the values of ![]() and
and ![]() -
- ![]() from
from ![]() to
to ![]()
Table 1.
| n | s |
|
n | |
|
| 1 | 0 | 0 | 9 | 3.328 | 13.14 |
| 2 | 0.25 | 0.25 | 10 | 3.863 | 18.13 |
| 3 | 0.577 | 0.58 | 11 | 4.416 | 23.60 |
| 4 | 0.957 | 1.41 | 12 | 4.984 | 30.80 |
| 5 | 1.377 | 2.43 | 13 | 5.565 | 38.57 |
| 6 | 1.828 | 4.25 | 14 | 6.159 | 48.38 |
| 7 | 2.305 | 6.35 | 15 | 6.764 | 58.83 |
| 8 | 2.805 | 9.56 | 16 | 7.379 | 71.65 |
We see from the table that the number of electrons which can rotate in a single
ring round a nucleus of charge ![]() increases only very slowly for increasing
increases only very slowly for increasing ![]() ; for
; for ![]() the maximum value is
the maximum value is ![]() ; for
; for ![]() ; for
; for ![]() ,
, ![]() . We see, further, that a ring of
. We see, further, that a ring of ![]() electrons cannot rotate in a single
ring round a nucleus of charge
electrons cannot rotate in a single
ring round a nucleus of charge ![]() unless
unless ![]() .
.
In the above we have suppose that the electrons move under the influence of a stationary radial force and that their orbits are exactly circular. The first condition will not be satisfied if we consider a system containing several rings of electrons which rotate with different frequencies. If, however, the distance between the rings is not small in comparison with their radii, if the ratio between their frequency is not near to unity, the deviation from circular orbits may be very small and the motion of the electrons to a close approximation may be identical with that obtained on the assumption that the charge on the electrons is uniformly distributed along the circumference of the rings. If the ratio between the radii of the rings is not near to unity, the conditions of stability on this assumption may also be considered sufficient.
We have assumed in ![]() that the electrons in the atoms rotate in coaxial
rings. The calculation indicated that only in the case of systems containing a
great number of electrons will the planes of the rings separate; in the case of
systems containing a moderate number of electrons, all the rings will be
situated in a single plane through the nucleus. For the sake of brevity, we
shall therefore here only consider the latter case.
that the electrons in the atoms rotate in coaxial
rings. The calculation indicated that only in the case of systems containing a
great number of electrons will the planes of the rings separate; in the case of
systems containing a moderate number of electrons, all the rings will be
situated in a single plane through the nucleus. For the sake of brevity, we
shall therefore here only consider the latter case.
Let us consider an electric charge ![]() uniformly distributed along the
circumference of a circle of radius
uniformly distributed along the
circumference of a circle of radius ![]() .
.
At a point distant ![]() from the plane of the ring, and at a distance
from the plane of the ring, and at a distance ![]() from
the axis of the ring, the electrostatic potential is given by
from
the axis of the ring, the electrostatic potential is given by
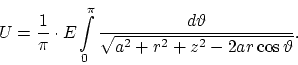
Putting in this expression
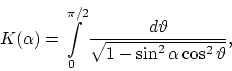
we get for the radial force exerted on an electron in a point in the plane of the ring
where
The corresponding force perpendicular to the plane of the ring at a distance ![]() from the center of the ring and at a small distance
from the center of the ring and at a small distance ![]() from its plane is
given by
from its plane is
given by
where
A short table of the functions
Next consider a system consisting of a number of concentric rings of electrons
which rotate in the same plane round a nucleus of charge ![]() . Let the radial of
the rings be
. Let the radial of
the rings be
![]() , and the number of electrons on the different
rings
, and the number of electrons on the different
rings
![]()
Putting
![]() we get for the radial
force acting on an electron in the
we get for the radial
force acting on an electron in the ![]() th ring
th ring ![]() where
where
the summation is to be taken over all the rings except the one considered.
If we know the distribution of the electrons in the different rings, from the
relation (1) on p. 478,???? we can, by help of the above, determine
![]() . The calculation can be made by successive approximations,
starting from a set of values for the
. The calculation can be made by successive approximations,
starting from a set of values for the ![]() '
'![]() , and from them calculating
the
, and from them calculating
the ![]() '
'![]() , and then redetermining the
, and then redetermining the ![]()
![]() by the relation (1) which
gives
by the relation (1) which
gives
![]() , and
so on.
, and
so on.
As in the case of a single ring it is supposed that the systems are stable for
displacements of the electrons in the plane of their orbits. In a calculation
such as that on p. 480,????? the interaction of the rings
ought strictly to be taken
into account. This interaction will involve that the quantities ![]() are not
constant, as for a single ring rotating round a nucleus, but will vary with the
radii of the rings; the variation in
are not
constant, as for a single ring rotating round a nucleus, but will vary with the
radii of the rings; the variation in ![]() , however, if the ratio between the
radii of the rings is not very near to unity, will be too small to be of
influence on the result of the calculation.
, however, if the ratio between the
radii of the rings is not very near to unity, will be too small to be of
influence on the result of the calculation.
Considering the stability of the systems for a displacement of the electrons
perpendicular to the plane of the rings, it is necessary to distinguish between
displacements in which the centres of gravity of the electrons in the single
rings are unaltered, and displacements in which all the electrons inside the
same ring are displaced in the same direction.
The condition of stability for the first kind of displacements is given by the
condition (5) on p. 481,???? if for every ring we
replace ![]() by a quantity
by a quantity ![]() determined by the condition that
determined by the condition that
![]() is equal to the
component perpendicular to the plane of the ring of the force - due to the
nucleus and the electrons in the other rings - acting on one of the electrons
if it has received a small displacement
is equal to the
component perpendicular to the plane of the ring of the force - due to the
nucleus and the electrons in the other rings - acting on one of the electrons
if it has received a small displacement ![]() . Using the same notation as
above, we get
. Using the same notation as
above, we get
If all the electrons in one of the rings are displaced in the same direction by help of extraneous forces, the displacement will produce corresponding displacements of the electrons in the other rings; and this interaction will be of influence on the stability. For example, consider a system of
The condition of stability is that this expression is positive for arbitrary values
The following Table. containing the values of ![]() and
and ![]() for
every fifth degree from
for
every fifth degree from
![]() to
to
![]() , gives an
estimate of the order of magnitude of these functions: -
, gives an
estimate of the order of magnitude of these functions: -
Table 2.
| |
|
|
|
| 20 | 0.132 | 0.001 | 0.002 |
| 25 | 0.217 | 0.005 | 0.011 |
| 30 | 0.333 | 0.021 | 0.048 |
| 35 | 0.490 | 0.080 | 0.217 |
| 40 | 0.704 | 0.373 | 1.549 |
| 45 | 1.000 | - | - |
| 50 | 1.420 | 1.708 | 4.438 |
| 55 | 2.040 | 1.233 | 1.839 |
| 60 | 3.000 | 1.093 | 1.301 |
| 65 | 4.599 | 1.037 | 1.115 |
| 70 | 7.548 | 1.013 | 1.041 |
![]() indicated the ratio between the radii of the rings
indicated the ratio between the radii of the rings
![]() . The values of
. The values of ![]() show
that unless the ratio of the radii of the rings is nearly unity the effect of
outer rings on the dimensions of inner rings is very small, and that the
corresponding effect of inner rings on outer is to neutralize approximately the
effect of a part of the charge on the nucleus corresponding to the number of
electrons on the ring. The values of
show
that unless the ratio of the radii of the rings is nearly unity the effect of
outer rings on the dimensions of inner rings is very small, and that the
corresponding effect of inner rings on outer is to neutralize approximately the
effect of a part of the charge on the nucleus corresponding to the number of
electrons on the ring. The values of ![]() show that the effect of outer
rings on the stability of inner - though greater than the effect on the
dimensions - is small, but that unless the ratio between the radii is very
great, the effect of inner rings on the stability of outer is considerably
greater than to neutralize a corresponding part of the charge of the nucleus.
show that the effect of outer
rings on the stability of inner - though greater than the effect on the
dimensions - is small, but that unless the ratio between the radii is very
great, the effect of inner rings on the stability of outer is considerably
greater than to neutralize a corresponding part of the charge of the nucleus.
The maximum number of electrons which the innermost ring can contain being
unstable is approximately equal to that calculated on p. 482 for a single ring
rotating round a nucleus. For the outer rings, however, we get considerably
smaller numbers than those determined by the condition (5) if we replace ![]() by
the total charge on the nucleus and on the electrons of inner rings.
by
the total charge on the nucleus and on the electrons of inner rings.
If system of rings rotating round a nucleus in a single plane is stable for small displacements of the electrons perpendicular to this plane, there will in general be no stable configurations of the rings, satisfying the condition of the constancy of the angular momentum of the electrons, in which all the rings are not situated in the plane. An exception occurs in the special case of two rings containing equal numbers of electrons; in this case there may be a stable configuration in which the two rings have equal radii and rotate in parallel planes at equal distances from the nucleus, the electrons in the one ring being situated just opposite the intervals between the electrons in the other ring. The latter configuration, however, is unstable if the configuration in which all the electrons in the two rings are arranged in a single ring is stable.
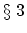 Constitution of Atoms containing very few Electrons
Constitution of Atoms containing very few Electrons
At stated in ![]() , the condition of the universal constancy of the angular
momentum of the electrons, together with the condition of stability, is in most
cases not sufficient to determine completely the constitution of the system. On
the general view of formation of atoms, however, and by making use of the
knowledge of the properties of the corresponding elements, it will be attempted
, in this section and the next, to obtain indications of what configurations of
the electrons may be expected to occur in the atoms. In these considerations we
shall assume that the number of electrons in the atom is equal to the number
which indicates the position of the corresponding element in the series of
elements arranged in order of increasing atomic weight.
, the condition of the universal constancy of the angular
momentum of the electrons, together with the condition of stability, is in most
cases not sufficient to determine completely the constitution of the system. On
the general view of formation of atoms, however, and by making use of the
knowledge of the properties of the corresponding elements, it will be attempted
, in this section and the next, to obtain indications of what configurations of
the electrons may be expected to occur in the atoms. In these considerations we
shall assume that the number of electrons in the atom is equal to the number
which indicates the position of the corresponding element in the series of
elements arranged in order of increasing atomic weight.
Exceptions to this rule will be supposed to occur only at such places in the series where deviation from the periodic law of the chemical properties of the elements are observed. In order to show clearly the principles used we shall first consider with some detail those atoms containing very few electrons.
Forsake of brevity we shall, by the symbol
![]() , refer to a
plane system of rings of electrons rotating round a nucleus of charge
, refer to a
plane system of rings of electrons rotating round a nucleus of charge ![]() ,
satisfying the condition of the angular momentum of the electrons with the
approximation used in
,
satisfying the condition of the angular momentum of the electrons with the
approximation used in ![]() .
.
![]() are the numbers of electrons in
the rings, starting from inside. By
are the numbers of electrons in
the rings, starting from inside. By
![]() and
and
![]() we shall denote the radii and frequency of the rings taken in the same
order. The total amount of energy
we shall denote the radii and frequency of the rings taken in the same
order. The total amount of energy ![]() emitted by the formation of the system
shall simply be denoted by
emitted by the formation of the system
shall simply be denoted by
![]() .
.
![]() Hydrogen.
Hydrogen.
In Part I. we have considered the binding of an electron by
a positive nucleus of
charge ![]() , and have shown that it is possible to account for the Balmer
spectrum of hydrogen on the assumption of the existence of a series of
stationary states in which the angular momentum of the electron round the
nucleus is equal to entire multiplies of the value
, and have shown that it is possible to account for the Balmer
spectrum of hydrogen on the assumption of the existence of a series of
stationary states in which the angular momentum of the electron round the
nucleus is equal to entire multiplies of the value ![]() , where
, where ![]() is Planck's constant. The formula found for the frequencies of the spectrum was
is Planck's constant. The formula found for the frequencies of the spectrum was
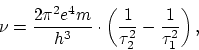
where
For the permanent state of a neutral hydrogen atom we get from the formula (1)
and (2) in ![]() , putting
, putting ![]() ,
,
These values are of the order of magnitude to be expected. For ![]() we
get 0.043, which corresponds to 13 volts; the value for the ionizing potential
of a hydrogen atom, calculated by Sir J.J. Thomson from experiments on positive
rays, is 11 volt.28No other definite data, however are available for hydrogen atoms. For sake of
brevity, we shall in the following denote the values for
we
get 0.043, which corresponds to 13 volts; the value for the ionizing potential
of a hydrogen atom, calculated by Sir J.J. Thomson from experiments on positive
rays, is 11 volt.28No other definite data, however are available for hydrogen atoms. For sake of
brevity, we shall in the following denote the values for ![]() and
and ![]() corresponding to the configuration 1(1) by
corresponding to the configuration 1(1) by ![]() , and
, and ![]() .
.
At distance from the nucleus, great in comparison with ![]() , the system 1
(1) will not exert sensible forces on free electrons. Since, however, the
configuration:
, the system 1
(1) will not exert sensible forces on free electrons. Since, however, the
configuration:
corresponds to a greater value for
![]() Helium.
Helium.
As shown in Part I., using the same assumptions as for hydrogen, we must expect
that during the binding of an electron by a nucleus of charge ![]() , a spectrum
is emitted, expressed by
, a spectrum
is emitted, expressed by
This spectrum includes the spectrum observed by Pickering in the star ![]() Puppis and the spectra recently observed by Folwer in experiments with vacuum
tubes filled with a mixture of hydrogen and helium. These spectra are generally
ascribed to hydrogen.
Puppis and the spectra recently observed by Folwer in experiments with vacuum
tubes filled with a mixture of hydrogen and helium. These spectra are generally
ascribed to hydrogen.
For the permanent state of a positively charge helium atom, we get
At distances from the nucleus great compared with the radius of the bound electron, the system 2(1) will, to a close approximation, act an an electron as a simple nucleus of charge
Since
we see that both electrons in a neutral helium atom are more firmly bound than the electron in a hydrogen atom. Using the values on p. 488,???? we get
these values are of the same order of magnitude as the value observed for the ionization potential in helium, 20.5 volt,29 and the value for the frequency of the ultra-violet absorption in helium determined by experiments on dispersion
The frequency in question may be regarded as corresponding to vibrations in the
plane of the ring (see p. 480).???? The frequency of vibration of the whole ring
perpendicular to the plane, calculated in the ordinary way (see p. 482), is
given by
![]() . The fact that the latter frequency is great
compared with that observed might explain that the number of electrons in a
helium atom, calculated by help of Drude's theory from the experiments on
dispersion, is only about two-thirds of the number to be expected. (Using
. The fact that the latter frequency is great
compared with that observed might explain that the number of electrons in a
helium atom, calculated by help of Drude's theory from the experiments on
dispersion, is only about two-thirds of the number to be expected. (Using
![]() the value calculated is 1.2.)
the value calculated is 1.2.)
For a configuration of a helium nucleus and three electrons, we get
Since
In a later paper it will be shown that the theory offers a simple explanation of the marked in the tendency of hydrogen and helium atoms to combine into molecules.
![]() Lithium.
Lithium.
In analogy with the cases of hydrogen and helium we must expect that during the
binding of an electron by a nucleus of charge ![]() , a spectrum is emitted, given
by
, a spectrum is emitted, given
by
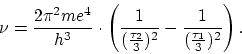
On account of the great energy to be spent in removing all the electrons bound in a lithium atom (see below) the spectrum considered can only be expected to be observed in extraordinary cases.
In a recent note Nicholson32 has drawn attention to the fact that in the spectra of
certain stars, which show the Pickering spectrum with special brightness, some
lines occur the frequencies of which to a close approximation can be expressed
by the formula
where
It is seen that the lines discussed by Nicholson are given by the above formula
if we put ![]() . The lines in question correspond to
. The lines in question correspond to
![]() and 14; if we for
and 14; if we for ![]() put
put
![]() and 15, we get lines
coinciding with lines of the ordinary Balmer-spectrum of hydrogen. If we
in the above formula put
and 15, we get lines
coinciding with lines of the ordinary Balmer-spectrum of hydrogen. If we
in the above formula put ![]() , and 3, we get series of lines in the
ultra-violet. If we put
, and 3, we get series of lines in the
ultra-violet. If we put ![]() we get only a single line in visible
spectrum, viz.: for
we get only a single line in visible
spectrum, viz.: for ![]() which gives
which gives
![]() , or a
wave-length
, or a
wave-length
![]() cm closely coinciding with
the wave-length
cm closely coinciding with
the wave-length
![]() cm of one of the lines of unknown
origin in the table quoted by Nicholson. In this table, however, no lines occur
corresponding to
cm of one of the lines of unknown
origin in the table quoted by Nicholson. In this table, however, no lines occur
corresponding to ![]() .
.
For the permanent state of a lithium atom with two positive charges we get a
configuration
The probably of a permanent configuration in which two electrons move in
different orbits around each other must for lithium be considered still less
probable than for helium, as the ratio between the radii of the orbits would be
still nearer to unity. For a lithium atom with a single positive charge we
shall, therefore, adopt the configuration:
Since
![]() we see that the first two
electrons in a lithium atom very strongly bound compared with the electron in a
hydrogen atom; they are still more rigidly bound than the electrons in a helium
atom.
we see that the first two
electrons in a lithium atom very strongly bound compared with the electron in a
hydrogen atom; they are still more rigidly bound than the electrons in a helium
atom.
>From a consideration of the chemical properties we should expect the following
configuration for the electrons in a neutral lithium atom:
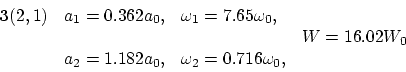
This configuration may be considered as highly probable also from a dynamical
point view. The deviation of the outermost electron from a circular orbit will
be very small, partly on account of the great values of the ratio between the
radii, and of the ratio between the frequencies of the orbits of the inner and
outer electrons, partly also on account of the symmetrical arrangement of the
inner electrons. accordingly, it appears probable that the three electrons will
not arrange themselves in a single ring and from the system:
although
Since ![]() [3(2,1) -
[3(2,1) - ![]() [3(2)] = 0.89W
[3(2)] = 0.89W![]() , we see that the outer
electron in the configuration 3(2,1) is bound even more lightly than the
electron in a hydrogen atom. the difference in the firmness of the binding
corresponds to a difference of 1.4 volts in the ionization potential. A marked
difference between the electron in hydrogen and the outermost electron in
lithium lies also in the greater tendency of the latter electron top leave
the plane of this orbits. The quantity
, we see that the outer
electron in the configuration 3(2,1) is bound even more lightly than the
electron in a hydrogen atom. the difference in the firmness of the binding
corresponds to a difference of 1.4 volts in the ionization potential. A marked
difference between the electron in hydrogen and the outermost electron in
lithium lies also in the greater tendency of the latter electron top leave
the plane of this orbits. The quantity ![]() considered in
considered in ![]() , which gives a
kind of measure for the stability for displacements perpendicular to this plane,
is thus for the outer electron in lithium only 0.55, while for hydrogen it is 1.
This may have a bearing on the explanation of the apparent tendency of lithium
atoms to take a positive charge in chemical combinations with other elements.
, which gives a
kind of measure for the stability for displacements perpendicular to this plane,
is thus for the outer electron in lithium only 0.55, while for hydrogen it is 1.
This may have a bearing on the explanation of the apparent tendency of lithium
atoms to take a positive charge in chemical combinations with other elements.
For a possible negatively charged lithium atom we may expect the configuration:
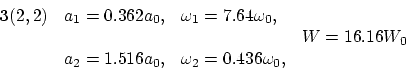
it should be remarked that we have no detailed knowledge of the properties in the atomic state, either for lithium or hydrogen, or for most of the electrons considered below.
![]() Beryllium.
Beryllium.
For reasons analogous to those considered for helium and lithium we may for the
formation of a neutral beryllium atom assume the following states:
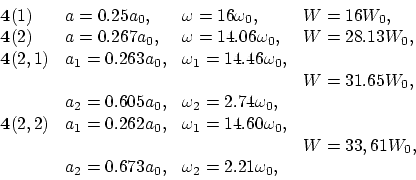
although the configurations:
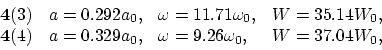
correspond to less values for the total energy than the configuration 4( 2,1) and 4(2,2).
>From analogy we get further for the configuration of a possible negatively
charged atom,
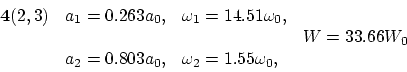
Comparing the outer ring of the atom considered with the ring of a helium atom,
we see that the presence of the inner ring of two electrons in the beryllium
atom markedly charges the properties of the outer ring; partly because the outer
electrons in the configuration adopted for a neutral beryllium atom are more
lightly bound than the electrons in a helium atom, and partly because the
quantity ![]() , which for helium is equal to 2, for the outer ring in the
configuration 4(2,2) is only equal 1.12.
, which for helium is equal to 2, for the outer ring in the
configuration 4(2,2) is only equal 1.12.
Since ![]() [4(2,3)] -
[4(2,3)] - ![]() [4(2,2)] = 0.05W
[4(2,2)] = 0.05W![]() , the beryllium atom
will further have a definite, although very small affinity for free electrons.
, the beryllium atom
will further have a definite, although very small affinity for free electrons.
 Atoms containing greater numbers of electrons
Atoms containing greater numbers of electrons
>From the examples discussed in the former section it will appear that the problem of the arrangement of the electrons in the atoms is intimately connected with the question of the confluence of two rings of electrons rotating round a nucleus outside each other, and satisfying the condition of the universal constancy of the angular momentum. apart from the necessary conditions of stability for displacements of the electrons perpendicular to the plane of the orbits, the present theory gives very little information on this problem. It seems, however, possible by the help of simple considerations to throw some light on the question.
Let us consider two rings rotating round a nucleus in a single plane, the one outside the other. Let us assume that the electrons in the one ring act upon the electrons in the other as if the electric charge were uniformly distributed along the circumference of the ring, and that the ring with this approximation satisfy the condition of the angular momentum of the electrons and stability for displacements perpendicular to their plane.
Now suppose that, by help of suitable imaginary extraneous forces acting parallel to the axis of the rings, we pull the inner ring slowly to one side. During this process, on account of the repulsion from the inner ring, the outer will move to the opposite side of the original plane of the rings. During the displacements of the rings angular momentum of the electrons round the axis of the system will remain constant, and the diameter of the inner ring will increase while that of the outer will diminish. At the beginning of the displacement the magnitude of the extraneous forces to be applied to the original inner ring will increase but thereafter decrease, and at a certain distance between the plane of the rings the system will be in a configuration of equilibrium. This equilibrium, however, will not be stable. If we let the rings slowly return they will either reach their original position, or they arrive at a position in which the ring, which originally was the outer, is now the inner, and vise versa.
If the charge of the electrons were uniformly distributed along the circumference of the rings, we could by the process considered at most obtain an interchange of the rings, but obviously not a junction of them. Taking, however, the discrete distribution of the electrons into account, it can be shown that in the special case when the number of electrons on the two rings are equal, and when the rings rotate in the same direction, the rings will unite by the process, provided that the final configuration is stable. In this case the radii and the frequency of the rings will be equal in the unstable configuration of equilibrium mentioned above. In reaching this configuration the electrons in the one ring will further be situated just opposite the intervals between the electrons in the outer, since such an arrangement will correspond to the smallest total energy. If now we let the rings return to their original plane, the electrons in the one ring will pass into the intervals between the electrons in the other, and from a single ring. Obviously the ring thus formed will satisfy the same condition of the angular momentum of the electrons as the original rings.
If the two rings contain unequal numbers of electrons the system will during a process such as that considered behave very differently, and, contrary to the former case, we cannot expect that the rings will flow together, if by help of extraneous forces acting parallel to the axis of the system they are displaced slowly from their original plane. It may in this connexion be noticed that the characteristic for the displacements considered is not the special assumption about the extraneous forces, but only invariance of the angular momentum of the electrons round the centre of the rings; displacements of this kind take in the present theory a similar position to arbitrary displacements in the ordinary mechanics.
The above considerations may be taken as an indication that there is greater
tendency for the confluence of two rings when each contains the same number of
electrons. Considering the successive binding of electrons by a positive
nucleus, we conclude from this that, unless the charge on the nucleus is very
great, rings of electrons will only join together if they contain equal numbers
of electrons; and that accordingly the numbers of electrons on inner rings will
only be 2, 4, 8, ![]() . If the charge of the nucleus is very great the rings
of electrons first bound, if few in number, will be very close together, and we
must expect that the configuration will be very unstable, and that a gradual
interchange of electrons between the rings will be greatly facilitated.
. If the charge of the nucleus is very great the rings
of electrons first bound, if few in number, will be very close together, and we
must expect that the configuration will be very unstable, and that a gradual
interchange of electrons between the rings will be greatly facilitated.
This assumption in regard to the number of electrons in the rings is strongly supported by the fact that the chemical properties of the elements of low atomic weight vary with a period of 8. Further, it follows that the number of electrons on the outermost ring will always be odd or even, according as the total number of electrons in the atom is add or even. This has a suggestive relation to the fact that the valency of an element of low atomic weight always is odd or even according as the number of the element in the periodic series is odd or even.
For the atoms of the elements considered in the former section we have assumed
that the two electrons first bound are arranged in a single ring, and, further,
that the two next electrons are arranged in another ring. If
![]() 4 the
configuration
4 the
configuration ![]() (4) will correspond to a smaller value for the total
energy than the configuration
(4) will correspond to a smaller value for the total
energy than the configuration ![]() (2,2). The greater the value of
(2,2). The greater the value of ![]() the
closer will the ratio between the radii of the rings in the configuration
the
closer will the ratio between the radii of the rings in the configuration ![]() (2,2) approach unity, and the greater will be the energy emitted by an
eventual confluence of the rings. The particular member of the series of the
elements for which the four innermost electrons will be arranged for the first
time in a single ring cannot be determined from the theory. From a consideration
of the chemical properties we can hardly expect that it will have taken place
before boron (
(2,2) approach unity, and the greater will be the energy emitted by an
eventual confluence of the rings. The particular member of the series of the
elements for which the four innermost electrons will be arranged for the first
time in a single ring cannot be determined from the theory. From a consideration
of the chemical properties we can hardly expect that it will have taken place
before boron (![]() = 5) or carbon
(
= 5) or carbon
(![]() = 6), on account of the observed
trivalency and tetravalency respectively of these elements; on the other hand,
the periodic system of the elements strongly suggests that already in neon
(
= 6), on account of the observed
trivalency and tetravalency respectively of these elements; on the other hand,
the periodic system of the elements strongly suggests that already in neon
(![]() = 10) an inner ring of eight electrons will occur. Unless
= 10) an inner ring of eight electrons will occur. Unless
![]()
![]() 14 the
configuration
14 the
configuration ![]() (4,4) corresponds to smaller value for the total energy
that the configuration
(4,4) corresponds to smaller value for the total energy
that the configuration ![]() (8); already for
(8); already for
![]()
![]() 10 the latter
configuration, however, will be stable for displacements of the electrons
perpendicular to the plane of their orbits. A ring of 16 electrons will not be
stable unless
10 the latter
configuration, however, will be stable for displacements of the electrons
perpendicular to the plane of their orbits. A ring of 16 electrons will not be
stable unless
![]() is very great; but in such a case the simple considerations
mentioned do not apply.
is very great; but in such a case the simple considerations
mentioned do not apply.
The confluence of two rings of equal number of electrons, which rotate round a
nucleus of charge ![]() outside a ring of
outside a ring of ![]() electrons already bound, must be
expected to take place more easily than the confluence of two similar rings
rotating round a nucleus of charge
electrons already bound, must be
expected to take place more easily than the confluence of two similar rings
rotating round a nucleus of charge
![]() ;
for the stability of the rings
for a displacement perpendicular to their plane will (see
;
for the stability of the rings
for a displacement perpendicular to their plane will (see ![]() ) be smaller in
the first than the latter case. This tendency for stability to decrease for
displacements perpendicular to the plane of the ring will be especially marked
for the outer rings of electrons of a neutral atom. In the latter case we must
expect the confluence of rings to be greatly facilitated and in certain cases it
may even happen that the number of electrons in the outer ring may be greater
than in the next, and that the outer ring may show deviations from the
assumption of 1, 2, 4, 8 electrons in the rings, e.g. the configurations 5(2,3) and 6(2,4) instead of the configuration 5(2,2,1) and 6(2,2,2). We shall here not discuss further the intricate question of the
arrangement of the electrons in the outer ring. In the scheme given below the
number of electrons in this rings is arbitrary put equal to the normal valency
of the corresponding element; i.e. for electronegative and electropositive
elements respectively the number of hydrogen atoms and twice the number of
oxygen atoms with which one atom of the element combines.
) be smaller in
the first than the latter case. This tendency for stability to decrease for
displacements perpendicular to the plane of the ring will be especially marked
for the outer rings of electrons of a neutral atom. In the latter case we must
expect the confluence of rings to be greatly facilitated and in certain cases it
may even happen that the number of electrons in the outer ring may be greater
than in the next, and that the outer ring may show deviations from the
assumption of 1, 2, 4, 8 electrons in the rings, e.g. the configurations 5(2,3) and 6(2,4) instead of the configuration 5(2,2,1) and 6(2,2,2). We shall here not discuss further the intricate question of the
arrangement of the electrons in the outer ring. In the scheme given below the
number of electrons in this rings is arbitrary put equal to the normal valency
of the corresponding element; i.e. for electronegative and electropositive
elements respectively the number of hydrogen atoms and twice the number of
oxygen atoms with which one atom of the element combines.
Such an arrangement of the outer electrons is suggested by considerations of
atomic volumes. As is well known, the atomic volume of the elements is a
periodic function of the atomic weights. If arranged in the usual way according
to the periodic system, the elements inside the same column have approximately
the same atomic volume, while this volume changes considerably from one column
to another, being greatest for columns corresponding to the smallest valency 1
and smallest for the greatest valency 4. An approximate estimate of the radius
of the outer ring of a neutral atom can be obtained by assuming that the total
forces due to the nucleus and the inner electrons is equal to that from a
nucleus of charge ![]() , where
, where ![]() is the number of electrons in the ring.
Putting
is the number of electrons in the ring.
Putting ![]() in the equation (1) on p. 478, ??????
and denoted the value of
in the equation (1) on p. 478, ??????
and denoted the value of ![]() for
for ![]() by
by ![]() , we get for
, we get for ![]() ,
, ![]() ; and for
; and for ![]()
![]() . According the arrangement chosen for the electrons will involve a
variation in the dimensions of the outer ring similar to the variation in the
atomic volumes of the corresponding elements. It must, however, be borne in mind
that the experimental determinations of atomic volumes in most cases are deduced
from consideration of molecules rather that atoms.
. According the arrangement chosen for the electrons will involve a
variation in the dimensions of the outer ring similar to the variation in the
atomic volumes of the corresponding elements. It must, however, be borne in mind
that the experimental determinations of atomic volumes in most cases are deduced
from consideration of molecules rather that atoms.
>From the above we are led to the following possible scheme for the arrangement
of the electrons in light atoms: -
| 1(1) | 9(4,4,1) | 17(8,4,4,1) |
| 2(2) | 10(8,2) | 18(8,8,2) |
| 3(2,1) | 11(8,2,1) | 19(8,8,2,1) |
| 4(2,2) | 12(8,2,2) | 20(8,8,2,2) |
| 5(2,3) | 13(8,2,3) | 21(8,8,2,3) |
| 6(2,4) | 14(8,2,4) | 22(8,8,2,4) |
| 7(4,3) | 15(8,4,3) | 23(8,8,4,3) |
| 8(4,2,2) | 16(8,4,2,2) | 24(8,8,4,2,2) |
Without any fuller discussion it seems not unlikely that this constitution of the atoms will correspond to properties of the elements similar with those observed.
In the first place there will be a marked periodicity with a period of 8. Further, the binding of the outer electrons in every horizontal series of the above scheme will become weaker with increasing number of electrons per atom, corresponding to the observed increase of the electropositive character for an increase of atomic weight of the elements in every single group of the periodic system. A corresponding agreement holds for the variation of the atomic volumes.
In the case of atoms of higher atomic weight the simple assumptions used do not
apply. A few indications, however, are suggested from consideration of the
variations in the chemical properties of the elements. At the end of the 3rd
period of 8 elements we meet with the iron-group. This group takes a
particular position in the system of the elements, since it is the first time
that elements of neighbouring atomic weight show similar chemical properties.
This circumstance indicates that the configurations of the electrons in the
elements of this group differ only in the arrangement of the inner electrons.
The fact that the period in the chemical properties of the elements after the
iron-group is no longer 8, but 18, suggests that elements of higher
atomic weight contain a recurrent configuration of 18 electrons in the innermost
rings. The deviation from 2, 4, 8, 16 may be due to a gradual interchange of
electrons between the rings, such as is indicated on p. 495. Since a ring of 18
electrons will not be stable the electrons may be arranged in two parallel rings
(see p. 486). ???????
Such a configuration of the inner electrons will act upon the
outer electrons in very nearly the same way as nucleus of charge
![]() . It
might therefore be possible that with increase of
. It
might therefore be possible that with increase of ![]() another configuration of
the same type will be formed outside the first, such as is suggested by the
presence of a second period of 18 elements.
another configuration of
the same type will be formed outside the first, such as is suggested by the
presence of a second period of 18 elements.
On the same lines, the presence of the group of the rare earths indicates that
for still greater values of ![]() another gradual alteration of the innermost
rings will take place. Since, however, for elements of higher atomic weight than
those of this group, the laws connection the vibration of the chemical
properties with the atomic weight are similar to these between the elements of
low atomic weight, we may conclude that the configuration of the innermost
electrons will be again repeated. The theory, however, is not sufficiently
complete to give a definite answer to such problems.
another gradual alteration of the innermost
rings will take place. Since, however, for elements of higher atomic weight than
those of this group, the laws connection the vibration of the chemical
properties with the atomic weight are similar to these between the elements of
low atomic weight, we may conclude that the configuration of the innermost
electrons will be again repeated. The theory, however, is not sufficiently
complete to give a definite answer to such problems.
 5 Characteristic Röntgen Radiation
5 Characteristic Röntgen Radiation
According to the theory of emission of radiation given in Part I., the ordinary line-spectrum of an element is emitted during the reformation of an atom when one or more of the electrons in the other rings are remover. In analogy it may be supposed that the characteristic Röntgen radiation is sent out during the setting down of the system if electrons in inner rings are removed by some agency, e.g. by impact of cathode particles. This view of the origin of the characteristic Röntgen radiation has been proposed by Sir. J.J. Thomson.
Without any special assumption in regard to the constitution of the radiation,
we can from this view determine the minimum velocity of the cathode rays
necessary to produce the characteristic Röntgen radiation of a spacial type by
calculating the energy necessary to remove one of the electrons from the
different rings. Even if we know the numbers of electrons in the rings, a
rigorous calculation of this momentum energy might still be complicated, and
the result largely dependent on the assumptions used; for, as mentioned in
Part I., p. 19, ??????????
the calculation cannot be performed entirely on the basis of the
ordinary mechanics. We can, however, obtain very simply an approximate
comparison with experiments if we consider the innermost ring and as a first
approximation neglect the repulsion from the electrons in comparison with the
attraction of the nucleus. Let us consider a simple system consisting of a bound
electron rotating in a circular orbit round a positive nucleus of charge ![]() .
>From the expressions (1) on p. 478 ???????
we get for the velocity of the electron, putting
.
>From the expressions (1) on p. 478 ???????
we get for the velocity of the electron, putting ![]() ,
,
The total energy to be transferred to the system in order to remove the
electron to an infinite distance from the nucleus is equal to the kinetic energy
of the bound electron. If, therefore, the electron is removed to a great
distance from the nucleus by impact of another rapidly moving electron, the
smallest kinetic energy possessed by the latter when at a great distance from
the nucleus must necessarily be equal to the kinetic energy of the bound
electron before the collision. The velocity of the free electron therefore
must be at least equal to ![]() .
.
According to Whiddington's
experiments33 the velocity of cathode rays just able to produce the
characteristic Röntgen radiation of the so-called
![]() -type-the
hardest type of radiation observed-from an element of atomic weight
-type-the
hardest type of radiation observed-from an element of atomic weight ![]() is
for elements from Al to Se approximately equal to
is
for elements from Al to Se approximately equal to ![]() cm/sec. As seen
this is equal to the above calculated value for
cm/sec. As seen
this is equal to the above calculated value for ![]() , if we put
, if we put ![]()
Since we have obtained approximate agreement with experiment by ascribing the
characteristic Röntgen radiation of the ![]() -type to the
innermost ring,
it is to be expected that no harder type of characteristic radiation will exist.
This is strongly indicated by observations of the penetrating power of
-type to the
innermost ring,
it is to be expected that no harder type of characteristic radiation will exist.
This is strongly indicated by observations of the penetrating power of
![]() rays.34
rays.34
It is worthy of remark that the theory gives not only nearly the right value for the energy required to remove an electron from the outer ring, but also the energy required to remove an electron from the innermost ring. The approximate agreement between the calculated and experimental values is all the more striking it is recalled that the energies required in the two cases for an element of atomic weight 70 differ by a ratio of 1000.
In connexion with this it should be emphasized that the remarkable homogeneity of the characteristic Röntgen radiation - indicated by experiments on absorption of the rays, as well as by the interference observed in recent experiments on diffraction of Röntgen rays in crystals - is in agreement with the main assumption used in part I. (see p. 7) in considering the emission of line-spectra, viz. that the radiation emitted during the passing of the systems between different stationary states is homogeneous.
Putting in (4) ![]() , we get for the diameter of the innermost ring
approximately
, we get for the diameter of the innermost ring
approximately
![]() cm. For
cm. For ![]() this gives
this gives ![]() cm, a value which is very small in comparison with ordinary atomic
dimensions but still very great compared with the dimensions to be expected for
the nucleus. according to Rutherford's calculation the dimensions of the
latter are of the same order of magnitude as
cm, a value which is very small in comparison with ordinary atomic
dimensions but still very great compared with the dimensions to be expected for
the nucleus. according to Rutherford's calculation the dimensions of the
latter are of the same order of magnitude as ![]() cm.
cm.
 Radioactive Phenomena
Radioactive Phenomena
According to the present theory the cluster of electrons surrounding the nucleus is formed with emission of energy, and the configuration is determined by the condition that the energy emitted is a maximum. The stability involved by these assumptions seems to be in agreement with the general properties of matter. It is, however, in striking opposition to the phenomena of radioactivity, and according to the theory the origin of the latter phenomena may therefore be sought elsewhere than in the electronic distribution round the nucleus.
A necessary consequence of Rutherford's theory of the structure of atoms is
that the ![]() -particles have their origin in the nucleus. On the
present theory it seems also necessary that the nucleus is the seat of the
expulsion of the high-speed
-particles have their origin in the nucleus. On the
present theory it seems also necessary that the nucleus is the seat of the
expulsion of the high-speed ![]() -particles. In the first place,
the spontaneous expulsion of a
-particles. In the first place,
the spontaneous expulsion of a ![]() -particle from the cluster of
electrons surrounding the nucleus would be something quite foreign to the
assumed properties of the system. further, the expulsion of an
-particle from the cluster of
electrons surrounding the nucleus would be something quite foreign to the
assumed properties of the system. further, the expulsion of an
![]() -particle can hardly be expected to
produce a lasting effect on the
stability of the cluster of electrons. The effect of the expulsion will be of
two different kinds. Partly the particle may collide with the bound electrons
during its passing through the atom. This effect will be analogous to that
produced by bombardment of atoms of other substances by
-particle can hardly be expected to
produce a lasting effect on the
stability of the cluster of electrons. The effect of the expulsion will be of
two different kinds. Partly the particle may collide with the bound electrons
during its passing through the atom. This effect will be analogous to that
produced by bombardment of atoms of other substances by ![]() -rays and
cannot be expected to give rise to a subsequent expulsion of
-rays and
cannot be expected to give rise to a subsequent expulsion of
![]() -rays. Partly the expulsion of the particle will involve an
alteration in the configuration of the bound electrons, since the charge
remaining on the nucleus is different from the original. In order to consider
the latter effect let us regard a single ring of electrons rotating round a
nucleus of charge
-rays. Partly the expulsion of the particle will involve an
alteration in the configuration of the bound electrons, since the charge
remaining on the nucleus is different from the original. In order to consider
the latter effect let us regard a single ring of electrons rotating round a
nucleus of charge ![]() , and let us assume that an
, and let us assume that an ![]() -particle is
expelled from the nucleus in a direction perpendicular to the plane of the ring.
The expulsion of the particle will obviously not produce any alteration in the
angular momentum of the electrons; and if the velocity of the
-particle is
expelled from the nucleus in a direction perpendicular to the plane of the ring.
The expulsion of the particle will obviously not produce any alteration in the
angular momentum of the electrons; and if the velocity of the
![]() -particle is small compared with the velocity of the electrons -
as it will be if we consider inner rings of an atom of high atomic
weight - the
ring during the expulsion will expand continuously, and after the expulsion
will take the position claimed by the theory for a stable ring rotating round a
nucleus of charge
-particle is small compared with the velocity of the electrons -
as it will be if we consider inner rings of an atom of high atomic
weight - the
ring during the expulsion will expand continuously, and after the expulsion
will take the position claimed by the theory for a stable ring rotating round a
nucleus of charge
![]() .
The consideration of this simple case strongly
indicates that the expulsion of an
.
The consideration of this simple case strongly
indicates that the expulsion of an ![]() -particle will not have a
lasting effect on the stability of the internal rings of electrons in
the residual atom.
-particle will not have a
lasting effect on the stability of the internal rings of electrons in
the residual atom.
The question of the origin of ![]() -particles may also be considered
from another point of view, based on a consideration of the chemical and
physical properties of the radioactive substances. As is well known, several of
these substances have very similar chemical properties and have hitherto
resisted every attempt to separate them by chemical means. There is also some
evidence that the substances in question show the same
line-spectrum.35 It has been suggested by several writers that the
substances are different only in radio-active properties and atomic
weight but identical in all other physical and chemical respects. according to
the theory, this would mean that the charge on the nucleus, as well as the
configuration of the surrounding electrons, was identical in some of the
elements, the only difference being the mass and the
internal condition of the
nucleus. From the considerations of
-particles may also be considered
from another point of view, based on a consideration of the chemical and
physical properties of the radioactive substances. As is well known, several of
these substances have very similar chemical properties and have hitherto
resisted every attempt to separate them by chemical means. There is also some
evidence that the substances in question show the same
line-spectrum.35 It has been suggested by several writers that the
substances are different only in radio-active properties and atomic
weight but identical in all other physical and chemical respects. according to
the theory, this would mean that the charge on the nucleus, as well as the
configuration of the surrounding electrons, was identical in some of the
elements, the only difference being the mass and the
internal condition of the
nucleus. From the considerations of ![]() this assumption is already strongly
suggested by the fact that the number of radioactive substances is greater than
the number of places at our disposal in the periodic system. If, however, the
assumption is right, the fact that two apparently identical elements emit
this assumption is already strongly
suggested by the fact that the number of radioactive substances is greater than
the number of places at our disposal in the periodic system. If, however, the
assumption is right, the fact that two apparently identical elements emit
![]() -particles of different velocities, shows that the
-particles of different velocities, shows that the
![]() -rays as well as the
-rays as well as the ![]() -rays have their origin in the
nucleus.
-rays have their origin in the
nucleus.
This view of the origin of ![]() - and
- and ![]() -particles explains very
simply the way in which the change in the chemical properties of the
radioactive substances is connected with the nature of the particles emitted.
The results of experiments are expressed in the two rules:-36
-particles explains very
simply the way in which the change in the chemical properties of the
radioactive substances is connected with the nature of the particles emitted.
The results of experiments are expressed in the two rules:-36
1. Whenever an ![]() -particles is expelled the group in
the periodic system to which the resultant product belongs is two
units less than that to which the parent body belongs.
-particles is expelled the group in
the periodic system to which the resultant product belongs is two
units less than that to which the parent body belongs.
2. Whenever a ![]() -particle is expelled the group of
the resultant body is 1 unit greater than that of the parent.
-particle is expelled the group of
the resultant body is 1 unit greater than that of the parent.
As will be seen this is exactly what is to be expected according
to the considerations of ![]() .
.
In escaping from the nucleus, the ![]() -rays may be
expected to collide with the bound electrons in the inner rings. This
will give rise to an emission of a characteristic radiation of the
same type as the characteristic Röntgen radiation emitted from elements
of lower atomic weight by impact of cathode-rays. The assumption that
the emission of
-rays may be
expected to collide with the bound electrons in the inner rings. This
will give rise to an emission of a characteristic radiation of the
same type as the characteristic Röntgen radiation emitted from elements
of lower atomic weight by impact of cathode-rays. The assumption that
the emission of ![]() -rays is due to collisions of
-rays is due to collisions of
![]() -rays with bound electrons is proposed by
Rutherford37 in order
to account for the numerous groups of homogeneous
-rays with bound electrons is proposed by
Rutherford37 in order
to account for the numerous groups of homogeneous ![]() -rays
expelled from certain radioactive substances.
-rays
expelled from certain radioactive substances.
In the present paper it has been attempted to show that the application of Planck's theory of radiation to Rutherford's atom-model through the introduction of the hypothesis of the universal constancy of the angular momentum of the bound electrons, leads to results which seem to be in agreement with experiments.
In a later paper the theory will be applied to systems containing more than one nucleus.
Footnotes
- ... Rutherford1
- E. Rutherford, Phil. Mag. XXI. p. 669 (1911)
- ... rays.2
- See also Geiger and Marsden, Phil. Mag. April 1913.
- ... Thomson3
- J.J. Thomson, Phil. Mag. VII. p. 237 (1904).
- ... size.4
- See f. inst., ``Theorie du ravonnement et les quanta.'' Rapports de la rennion a Bruxeless, Nov. 1911, Paris, 1912.
- ... constant.5
- See f. inst., M. Planck, Ann. d. Phys. XXXI. p. 758 (1910); XXXVII. p. 612 (1912); Verh. Phys. Ges. 1911, p. 138.
- ... Einstein.6
- A. Einstein, Ann. d.Phys. XVII. p. 132 (1905); XX. p. 199 (1906); XXII. p. 180 (1907).
- ... Haas,7
- A.E. Haas, Jahrb. d. Rad. u.El. VII. p. 261 (1910). See further, A.Schidlof, Ann. d. Phys. XXXV. p. 90 ( 1911); E. Wertheimer, Phys. Zietschr. XII. p. 409 (1911), Verh. deutsch. Phys. Ges. 1912, p. 431; F.A. Lindermann, Verh.deutsch.Phys.Ges. 1911, pp. 482, 1107; F. Haber, Verh. deutsch. Phys. Ges. 1911, p. 1117.
- ... Nicholson.8
- J.W. Nicholson, Month. Not. Roy. Astr. Soc. LXXII. pp. 49, 139, 677, 693, 729 (1912).
- ....9
- See f. inst. N. Bohr, Phil. Mag. XXV. p. 24 (1913). The conclusion drawn in the paper cited in strongly supported by the fact that hydrogen, in the experiments on positive rays of Sir. J.J. Thomson, is the only element which never occurs with a positive charge corresponding to the lose of more than one electron (comp. Phil. Mag. XXIV. p. 672 (1912).
- ... Paschen10
- F. Paschen, Ann. d. Phys. XXVII. p.565 (1908).
- ... Pickering11
- E.C. Pickering, Astrophys. J. IV. p. 369 (1896); v. p. 92 ( 1897).
- ... Fowler12
- A. Fowler, Mouth. Not. Roy. Astr. Soc. LXXIII. Dec. 1912.
- ... Ritz13
- W. Ritz, Phys. Zeitschr. IX. p. 521 (1908).
- ... Nicholson.14
- J.W. Nicholson, loc. cit. p. 679.
- ... Einstein15
- A. Einstein, Ann. d. Phys. XVII. p. 146 (1905).
- ... Wood16
- R.W. Wood, Physical Optics, p. 513 (1911).
- ... particles.17
- Compare J.J. Thomson, Phil. Mag. XXIII. p. 456 (1912).
- ... Rutherford.18
- E. Rutherford, Phil. Mag. XXIV. pp. 453 & 893 (1912).
- ... Thomson19
- Loc. cit.
- ... Nicholson.20
- Loc. cit.
- ... constant.''21
- In the considerations leading to this hypothesis we have assumed that the velocity of the electrons is small compared with the velocity of light. The limits of the validity of this assumption will be discussed in Part II.
- ... Nucleus22
- Part I was published in Phil. Mag. XXVI. p. 1 (1913).
- ... Ru\-ther\-ford23
- Comp. also Geiger and Marsden, Phil. Mag. XXV. p. 604 (1913).
- ... radiation.24
- Comp. C.G. Barkla, Phil. Mag. XXI. p. 648 (1911).
- ... hypothesis25
- Comp. A.v.d. Broek, Phys. Zeitschr. XIV. p. 32 (1913).
- ... considerations.26
- Comp. J.W. Nicholson, Month. Not. Roy. Astr. Soc. 72. p. 52 (1912).
- ...; 27
- This value is that calculated
in the first part of the paper.
Using the values
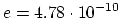 (see R.A. Millikan, Brit. Assoc. Rep.
1912, p. 410),
(see R.A. Millikan, Brit. Assoc. Rep.
1912, p. 410),
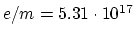 (see P. Gmelin, Ann. d. Phys.
XXVIII. p. 1086 (1909) and A.H. Bucherer, Ann. d. Phys.
XXXVII p. 597 (1912)), and
(see P. Gmelin, Ann. d. Phys.
XXVIII. p. 1086 (1909) and A.H. Bucherer, Ann. d. Phys.
XXXVII p. 597 (1912)), and
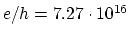 calculated by Planck's theory from the
experiments of E. Warbung G. Leithauser, E. Hupka,
and C. Muller, Ann.d.Phys. XL.
p. 611 (1913)) we get
calculated by Planck's theory from the
experiments of E. Warbung G. Leithauser, E. Hupka,
and C. Muller, Ann.d.Phys. XL.
p. 611 (1913)) we get
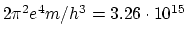 in very
close agreement with observations.
in very
close agreement with observations.
- ... volt.28
- J.J. Thomson, Phil. Mag. XXIV. p. 218 (1912).
- ... volt,29
- J.Franck u. G. Hertz, Verb. d. Deutsch. Phys. Ges. XV. p. 34 (1913).
- ...#tex2html_wrap_inline1450#30
- C. and M. Cuthbertson, Proc. Roy. Soc. A. LXXXIV. p. 13 (1910). In a previous paper (Phil. Mag. Jan. 1913) the author took the values for the refractive index in helium, given by M. and C. Cuthbertson, as corresponding to atmosphere pressure; these values, however, refer to double atmosphere pressure. Consequently the value there given for the number of electrons in a helium atom calculated from Drude's theory has to be divided by 2.)
- ... electrons.31
- See J. Franck, Verh. d. Deutsch. Phys. Ges. XII. p. 613 (1910).
- ... Nicholson32
- J.W. Nicholson, Month. Not. Roy. Astr. Soc. LXXIII. 382 (1913).
- ... experiments33
- R. Whiddington, Proc. Roy. Soc. A. LXXXV. p. 323 (1911).
- ... rays.34
- Comp. E. Rutherford, Phil. Mag. XXIV. p. 453 (1912).
- ...line-spectrum.35
- see A.S. Russel and R. Rossi, Proc. Roy. Soc. A. LXXXVII. p. 478 (1912).
- ... rules:-36
- See A.S. Russell, Chem. News, CVII. p. 49 (1913); G.v. Hevesy, Phys. Zeitschr. XIV. p. 49 (1913); K. Fajaus, Phys. Zeitschr. XIV. pp. 131 & 136 (1913); Verh. d. deutsch. Phys. Ges. XV. p. 240 (1913); F. Soddy, Chem. News, CVII. p. 97 (1913).
- ... Rutherford37
- E. Rutherford, Phil. Mag. XXIV. pp. 453&893 (1912).