Bájatelo

El magnetismo como efecto relativista

Barbol

2003

En los principios de la física existía una parte de ella que se dedicaba a estudiar la electricidad, causada por las cargas, y otra dedicada a estudiar el magnetismo, creada por los imanes. Con el pasar del tiempo se fue descubriendo que el magnetismo era capaz de crear electricidad (ley de Faraday) y, con Maxwell, que la electricidad puede crear magnetismo. Se debía, por tanto, de hablar de una única fuerza electromagnética, pues ambas estaban interrelacionadas.

Sin embargo había un problema, el electromagnetismo no era invariante bajo transformaciones de Galileo, pero sí bajo transformaciones de Lorentz (lo que no debe sorprender, pues fueron creadas para que el electromagnetismo fuese invariante). Esas transformaciones de Lorentz son las mismas a las que llegó Einstein tras suponer que la velocidad de la luz es constante y de igual valor en cualquier sistema de referencia inercial, en lo que se conoce como teoría de la relatividad.

Por tanto, vemos que el electromagnetismo era, antes de Einstein, ya de por si relativista.

La electrostática estudiaba los campos y fuerzas creados por cargas estáticas y el magnetismo los campos y fuerzas creados por corrientes, que no son otra cosa que cargas en movimiento... sin embargo tenía que haber una relación entre ambas: si nos movemos a la misma velocidad que las cargas de las corrientes se tienen que cumplir las leyes de la electrostática. Como ya se dijo antes las transformaciones de Galileo no servían, se tuvieron que emplear las de Lorentz.

Presento aquí un pequeño ejemplo de cómo se hace esto, basado en el libro de Física general de Días de Deus.

Supongamos que tenemos un cable en un laboratorio. Vamos a suponer también que este cable tiene una sección conocida y que por él hacemos circular una corriente. Esta corriente se puede considerar como un flujo de electrones que, en media, se mueven a velocidad $\vec{v}$ .

En una sección finita de cable de longitud tendremos, en general, igual número de cargas positivas como negativas, con lo que la carga neta es nula, es decir $Q=(\rho_{+}+\rho_{-})SL=0$ . De aquí sacamos dos importantes consecuencias para nuestro estudio. En el sistema de referencia del laboratorio, en el cual el cable está quieto y los electrones se mueven a velocidad $\vec{v}$ tenemos:

$\begin{displaymath} (\rho_{+}+\rho_{-})SL=0\Rightarrow\rho_{+}=-\rho_{-} \qquad Q=0\Rightarrow\vec{E}=0 \end{displaymath}$

Ahora supongamos que nos ponemos en el sistema de referencia en el cual los electrones están quietos. En este caso son los protones y el cable los que se mueven a una velocidad $\vec{v'}=-\vec{v}$ .

La totalidad de las cargas positivas en el hilo de longitud en el sistema del laboratorio (el cable quieto) es $Q_{+}=\rho_{+}SL$ , mientras que en el sistema en el cual los electrones están en reposo es $Q'_{+}=\rho'_{+}SL'$ . Donde las áreas son iguales por ser perpendiculares a la dirección del movimiento de las cargas.

Experimentalmente se ha determinado que la carga eléctrica es una invariante en relatividad, por lo que tenemos que, para la densidad de carga positiva, $Q_{+}=Q'_{+}\Rightarrow\rho_{+}L=\rho'_{+}L'$ .

Podemos relacionar y mediante la contracción de Lorentz, que nos dice que $L'=L\sqrt{1-v^{2}/c^{2}}$ , por lo que obtenemos el valor de $\rho'_{+}$ del siguiente modo:

$\begin{displaymath} \rho_{+}L=\rho'_{+}L'\Rightarrow\rho'_{+}=\frac{\rho_{+}L}{L'}=\frac{\rho_{+}}{\sqrt{1-v^{2}/c^{2}}} \end{displaymath}$

Lo mismo podemos hacer con la densidad de carga negativa, $Q_{-}=Q'_{-}\Rightarrow\rho_{-}L=\rho'_{-}L'$ .

Ahora tenemos que tener cuidado, porque en este caso es la longitud en el referencial en que las cargas están en reposo y la longitud para el referencial en el que las cargas se mueven, por tanto $L=L'\sqrt{1-v^{2}/c^{2}}$ , de aquí:

$\begin{displaymath} \rho_{-}L=\rho'_{-}L'\Rightarrow\rho'_{-}=\frac{\rho_{-}L}{L'}=\rho_{-}\sqrt{1-v^{2}/c^{2}} \end{displaymath}$

Y la densidad total de carga es

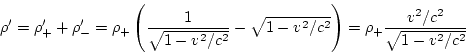
$\begin{displaymath} \rho'=\rho'_{+}+\rho'_{-}=\rho_{+}\left(\frac{1}{\sqrt{1-v^{... ...c^{2}}\right)=\rho_{+}\frac{v^{2}/c^{2}}{\sqrt{1-v^{2}/c^{2}}} \end{displaymath}$

Vemos, por tanto, que merced a la conservación de la carga y a la contracción de Lorentz un cable neutro cuando está quito tiene, en general, una densidad de carga distinta de cero cuando el referencial se desplaza respecto a él.

Entonces, según el teorema de Gauss, esta densidad de carga creará un campo eléctrico diferente de cero, el cual crea una fuerza sobre una carga de prueba de la forma:

$\begin{displaymath} F'=qE'=\frac{q\rho_{+}A(v^{2}/c^{2})}{2\pi\varepsilon_{0}r\sqrt{1-v^{2}/c^{2}}} \end{displaymath}$

Veamos cómo se manifiesta esta fuerza en el referencial en el que el cable está quieto. Según la segunda ley de Newton $\vec{F}=d\vec{p}/dt$ y $\vec{F'}=d\vec{p'}/dt'$ . $\vec{p}=\vec{p'}$ son vectores perpendiculares al movimiento, y según la ecuación de dilatación temporal $dt=dt'/\sqrt{1-v^{2}/c^{2}}$ , por lo que

$\begin{displaymath} \vec{F}=\vec{F'}\sqrt{1-v^{2}/c^{2}}=\frac{qv^{2}\rho_{+}S}{... ...frac{qIv}{2\pi\varepsilon_{0}c^{2}r}=\frac{\mu_{0}qIv}{2\pi r} \end{displaymath}$

Ya que $I=\rho vS$ y $\mu_{0}=1/\varepsilon_{o}c^{2}$ . Como vemos, aunque en el laboratorio no hay campo eléctrico hay una fuerza asociada al campo eléctrico del referencial en el que los electrones se mueven, y que coincide con el resultado observado del magnetismo... ¡son el mismo!

Acceso rápido