the Emission and Transformation of Light
Bern, 17 March 1905
(Received March 18, 1905)
American Journal of Physics, v. 33, n. 5, May 1965
A profound formal distinction exists between the theoretical concepts which physicists have formed regarding gases and other ponderable bodies and the Maxwellian theory of electromagnetic processes in so-called empty space. While we consider the state of a body to be completely determined by the positions and velocities of a very large, yet finite, number of atoms and electrons, we make use of continuous spatial functions to describe the electromagnetic state of a given volume, and a finite number of parameters cannot be regarded as sufficient for the complete determination of such a state. According to the Maxwellian theory, energy is to be considered a continuous spatial function in the case of all purely electromagnetic phenomena including light, while the energy of a ponderable object should, according to the present conceptions of physicists, be represented as a sum carried over the atoms and electrons. The energy of a ponderable body cannot be subdivided into arbitrarily many or arbitrarily small parts, while the energy of a beam of light from a point source (according to the Maxwellian theory of light or, more generally, according to any wave theory) is continuously spread an ever increasing volume.
The wave theory of light, which operates with continuous spatial functions, has worked well in the representation of purely optical phenomena and will probably never be replaced by another theory. It should be kept in mind, however, that the optical observations refer to time averages rather than instantaneous values. In spite of the complete experimental confirmation of the theory as applied to diffraction, reflection, refraction, dispersion, etc., it is still conceivable that the theory of light which operates with continuous spatial functions may lead to contradictions with experience when it is applied to the phenomena of emission and transformation of light.
It seems to me that the observations associated with blackbody radiation, fluorescence, the production of cathode rays by ultraviolet light, and other related phenomena connected with the emission or transformation of light are more readily understood if one assumes that the energy of light is discontinuously distributed in space. In accordance with the assumption to be considered here, the energy of a light ray spreading out from a point source is not continuously distributed over an increasing space but consists of a finite number of energy quanta which are localized at points in space, which move without dividing, and which can only be produced and absorbed as complete units.
In the following I wish to present the line of thought and the facts which have led me to this point of view, hoping that this approach may be useful to some investigators in their research.
1. Concerning a Difficulty with Regard to the Theory of Blackbody Radiation
We start first with the point of view taken in the Maxwellian and the electron theories and consider the following case. In a space enclosed by completely reflecting walls, let there be a number of gas molecules and electrons which are free to move and which exert conservative forces on each other on close approach: i.e. they can collide with each other like molecules in the kinetic theory of gases.1 Furthermore, let there be a number of electrons which are bound to widely separated points by forces proportional to their distances from these points. The bound electrons are also to participate in conservative interactions with the free molecules and electrons when the latter come very close. We call the bound electrons ``oscillators'': they emit and absorb electromagnetic waves of definite periods.
According to the present view regarding the origin of light, the radiation in the space we are considering (radiation which is found for the case of dynamic equilibrium in accordance with the Maxwellian theory) must be identical with the blackbody radiation -- at least if oscillators of all the relevant frequencies are considered to be present.
For the time being, we disregard the radiation emitted and absorbed by
the oscillators and inquire into the condition of dynamical
equilibrium associated with the interaction (or collision) of
molecules and electrons. The kinetic theory of gases asserts that the
average kinetic energy of an oscillator electron must be equal to the
average kinetic energy of a translating gas molecule. If we separate
the motion of an oscillator electron into three components at angles
to each other, we find for the average energy ![]() of one
of these linear components the expression
of one
of these linear components the expression
where
We shall now proceed to present a similar argument regarding the interaction
between the oscillators and the radiation present in the cavity. Herr Planck has
derived2 the condition for the
dynamics equilibrium in this case under the supposition that the radiation can
be considered a completely random process.3 He found
where
If the radiation energy of frequency ![]() is
not continually increasing or
decreasing, the following relations must obtain:
is
not continually increasing or
decreasing, the following relations must obtain:
These relations, found to be the conditions of dynamic equilibrium, not only fail to coincide with experiment, but also state that in our model there can be not talk of a definite energy distribution between ether and matter. The wider the range of wave numbers of the oscillators, the greater will be the radiation energy of the space, and in the limit we obtain
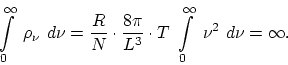
2. Concerning Planck's Determination of the Fundamental Constants
We wish to show in the following that Herr Planck's determination of the fundamental constants is, to a certain extent, independent of his theory of blackbody radiation.
Planck's formula,4 which has
proved adequate up to this point, gives for ![]()
For large values of
It is evident that this equation is identical with the one obtained in Sec. 1 from the Maxwellian and electron theories. By equating the coefficients of both formulas one obtains
or
i.e., an atom of hydrogen weighs
We therefore arrive at the conclusion: the greater the energy density and the wavelength of a radiation, the more useful do the theoretical principles we have employed turn out to be: for small wavelengths and small radiation densities, however, these principles fail us completely.
In the following we shall consider the experimental facts concerning blackbody radiation without invoking a model for the emission and propagation of the radiation itself.
3. Concerning the Entropy of Radiation
The following treatment is to be found in a famous work by Herr W. Wien and is introduced here only for the sake of completeness.
Suppose we have radiation occupying a volume ![]() . We assume that the observable
properties of the radiation are completely determined when the radiation density
. We assume that the observable
properties of the radiation are completely determined when the radiation density
![]() is given for all frequencies.5 Since radiation of different frequencies are
to be considered independent of each other when there is no transfer of heat or
work, the entropy of the radiation can be represented by
is given for all frequencies.5 Since radiation of different frequencies are
to be considered independent of each other when there is no transfer of heat or
work, the entropy of the radiation can be represented by
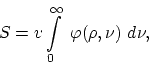
where
![]() can be reduced to a function of a single variable through
formulation of the condition that the entropy of the radiation is
unaltered during adiabatic compression between reflecting walls. We
shall not enter into this problem, however, but shall directly
investigate the derivation of the function
can be reduced to a function of a single variable through
formulation of the condition that the entropy of the radiation is
unaltered during adiabatic compression between reflecting walls. We
shall not enter into this problem, however, but shall directly
investigate the derivation of the function
![]() from the blackbody
radiation law.
from the blackbody
radiation law.
In the case of blackbody radiation, ![]() is such
a function of
is such
a function of ![]() that the
entropy is maximum for a fixed value of energy; i.e.,
that the
entropy is maximum for a fixed value of energy; i.e.,
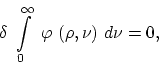
providing
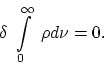
>From this it follows that for every choice of ![]() as a function of
as a function of
![]()
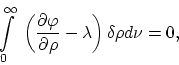
where
The following equation applies when the temperature of a unit volume of
blackbody radiation increases by ![]()
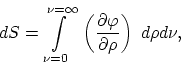
or, since
Since
By comparison one obtains
This is the law of blackbody radiation. Therefore one can derive the law of
blackbody radiation from the function
![]() , and, inversely, one can derive the
function
, and, inversely, one can derive the
function ![]() by integration, keeping in mind the fact
that
by integration, keeping in mind the fact
that ![]() vanishes
when
vanishes
when ![]() .
.
4. Asymptotic from for the Entropy of Monochromatic Radiation at Low Radiation Density
>From existing observations of the blackbody radiation, it is clear that the law
originally postulated by Herr W. Wien,
is not exactly valid. It is, however, well confirmed experimentally for large values of
This formula gives immediately
and then, by using the relation obtained in the preceeding section,
Suppose that we have radiation of energy
If we confine ourselves to investigating the dependence of the entropy on the
volume occupied by the radiation, and if we denote by ![]() the entropy of the
radiation at volume
the entropy of the
radiation at volume ![]() , we obtain
, we obtain
This equation shows that the entropy of a monochromatic radiation of sufficiently low density varies with the volume in the same manner as the entropy of an ideal gas or a dilute solution. In the following, this equation will be interpreted in accordance with the principle introduced into physics by Herr Boltzmann, namely that the entropy of a system is a function of the probability its state.
5. Molecular-Theoretic Investigation of the Dependence of the Entropy of Gases and Dilute solutions on the volume
In the calculation of entropy by molecular-theoretic methods we frequently use the word ``probability'' in a sense differing from that employed in the calculus of probabilities. In particular ``gases of equal probability'' have frequently been hypothetically established when one theoretical models being utilized are definite enough to permit a deduction rather than a conjecture. I will show in a separate paper that the so-called ``statistical probability'' is fully adequate for the treatment of thermal phenomena, and I hope that by doing so I will eliminate a logical difficulty that obstructs the application of Boltzmann' s Principle. here, however, only a general formulation and application to very special cases will be given.
If it is reasonable to speak of the probability of the state of a system, and
futhermore if every entropy increase can be understood as a transition to a
state of higher probability, then the entropy ![]() of a system is a function of
of a system is a function of
![]() , the probability of its instantaneous state. If we have two
noninteracting systems
, the probability of its instantaneous state. If we have two
noninteracting systems ![]() and
and ![]() , we can write
, we can write
If one considers these two systems as a single system of entropy
and
The last equation says that the states of the two systems are independent of each other.
>From these equation it follows that
and finally
The quantity
First we treat the following special case. We consider a number
This system, which, for example, can be an ideal gas or a dilute solution,
possesses an entropy ![]() . Let us imagine transferring all
. Let us imagine transferring all ![]() movable points
into a volume
movable points
into a volume ![]() (part of the volume
(part of the volume ![]() ) without anything else being changed
in the system. This state obviously possesses a different entropy
) without anything else being changed
in the system. This state obviously possesses a different entropy ![]() , and now
wish to evaluate the entropy difference with the help of the Boltzmann
Principle.
, and now
wish to evaluate the entropy difference with the help of the Boltzmann
Principle.
We inquire: How large is the probability of the latter state relative to the
original one? Or: How large is the probability that at a randomly chosen instant
of time all ![]() movable points in the given volume
movable points in the given volume ![]() will be found by chance
in the volume
will be found by chance
in the volume ![]() ?
?
For this probability, which is a ``statistical probability'', one obviously
obtains:
By applying the Boltzmann Principle, one then obtains
It is noteworthy that in the derivation of this equation, from which one can easily obtain the law of Boyle and Gay-Lussac as well as the analogous law of osmotic pressure thermodynamically,6 no assumption had to be made as to a law of motion of the molecules.
6. Interpretation of the Expression for the volume Dependence of the entropy of Monochromatic Radiation in Accordance with Boltzmann's Principle
In Sec. 4, we found the following expression for the dependence of the entropy
of monochromatic radiation on the volume
If one writes this in the from
and if one compares this with the general formula for the Boltzmann principle
one arrives at the following conclusion:
If monochromatic radiation of frequency ![]() and energy
and energy ![]() is enclosed by
reflecting walls in a volume
is enclosed by
reflecting walls in a volume ![]() , the probability that the total radiation
energy will be found in a volume
, the probability that the total radiation
energy will be found in a volume ![]() (part of the volume
(part of the volume ![]() ) at any randomly
chosen instant is
) at any randomly
chosen instant is
>From this we further conclude that: Monochromatic radiation of low density (
within the range of validity of Wien's radiation formula) behaves
thermodynamically as though it consisted of a number of independent energy
quanta of magnitude ![]() .
.
We still wish to compare the average magnitude of the energy quanta of the
blackbody radiation with the average translational kinetic energy of a molecule
at the same temperature. The latter is
![]() , while,
according to the Wien formula, one obtains for the average magnitude of an
energy quantum
, while,
according to the Wien formula, one obtains for the average magnitude of an
energy quantum
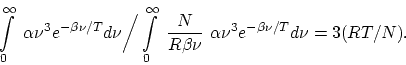
If the entropy of monochromatic radiation depends on volume as though the
radiation were a discontinuous medium consisting of energy quanta of magnitude ![]() , the next obvious step is to investigate whether the laws of
emission and transformation of light are also of such a nature that they can be
interpreted or explained by considering light to consist of such energy quanta.
We shall examine this question in the following.
, the next obvious step is to investigate whether the laws of
emission and transformation of light are also of such a nature that they can be
interpreted or explained by considering light to consist of such energy quanta.
We shall examine this question in the following.
7. Concerning Stokes's Rule
According to the result just obtained, let us assume that, when monochromatic
light is transformed through photoluminescence into light of a different
frequency, both the incident and emitted light consist of energy quanta of
magnitude ![]() , where
, where ![]() denotes the relevant frequency. The
transformation process is to be interpreted in the following manner. Each
incident energy quantum of frequency
denotes the relevant frequency. The
transformation process is to be interpreted in the following manner. Each
incident energy quantum of frequency ![]() is absorbed and generates by
itself-at least at sufficiently low densities of incident energy quanta - a
light quantum of frequency
is absorbed and generates by
itself-at least at sufficiently low densities of incident energy quanta - a
light quantum of frequency ![]() ; it is possible that the absorption of the
incident light quanta can give rise to the simultaneous emission of light quanta
of frequencies
; it is possible that the absorption of the
incident light quanta can give rise to the simultaneous emission of light quanta
of frequencies ![]() etc., as well as to energy of other kinds, e.g.,
heat. It does not matter what intermediate processes give rise to this final
result. If the fluorescent substance is not a perpetual source of energy, the
principle of conservation of energy requires that the energy of an emitted
energy quantum cannot be greater than that of the incident light quantum; it
follows that
etc., as well as to energy of other kinds, e.g.,
heat. It does not matter what intermediate processes give rise to this final
result. If the fluorescent substance is not a perpetual source of energy, the
principle of conservation of energy requires that the energy of an emitted
energy quantum cannot be greater than that of the incident light quantum; it
follows that
or
This is the well-known Stokes's Rule.
It should be strongly emphasized that according to our conception the quantity of light emitted under conditions of low illumination (other conditions remaining constant) must be proportional to the strength of the incident light, since each incident energy quantum will cause an elementary process of the postulated kind, independently of the action of other incident energy quanta. In particular, there will be no lower limit for the intensity of incident light necessary to excite the fluorescent effect.
According to the conception set forth above, deviations from Stokes's Rule are conceivable in the following cases:
1. when the number of simultaneously interacting energy quanta per unit volume is so large that an energy quantum of emitted light can receive its energy from several incident energy quanta;
2. when the incident (or emitted) light is not of such a composition that it corresponds to blackbody radiation within the range of validity of Wien's Law, that is to say, for example, when the incident light is produced by a body of such high temperature that for the wavelengths under consideration Wien's Law is no longer valid.
The last-mentioned possibility commands especial interest. According to the conception we have outlined, the possibility is not excluded that a ``non-Wien radiation'' of very low density can exhibit an energy behavior different from that of a blackbody radiation within the range of validity of Wien's Law.
8. Concerning the Emission of Cathode Rays
Through Illumination of
Solid Bodies
The usual conception that the energy of light is continuously distributed over the space through which it propagates, encounters very serious difficulties when one attempts to explain the photoelectric phenomena, as has been pointed out in Herr Lenard's pioneering paper.7
According to the concept that the incident light consists of energy quanta of
magnitude ![]() , however, one can conceive of the ejection of
electrons by light in the following way. Energy quanta penetrate into the
surface layer of the body, and their energy is transformed, at least in part,
into kinetic energy of electrons. The simplest way to imagine this is that a
light quantum delivers its entire energy to a single electron: we shall assume
that this is what happens. The possibility should not be excluded, however, that
electrons might receive their energy only in part from the light quantum.
, however, one can conceive of the ejection of
electrons by light in the following way. Energy quanta penetrate into the
surface layer of the body, and their energy is transformed, at least in part,
into kinetic energy of electrons. The simplest way to imagine this is that a
light quantum delivers its entire energy to a single electron: we shall assume
that this is what happens. The possibility should not be excluded, however, that
electrons might receive their energy only in part from the light quantum.
An electron to which kinetic energy has been imparted in the interior of the
body will have lost some of this energy by the time it reaches the surface.
Furthermore, we shall assume that in leaving the body each electron must perform
an amount of work ![]() characteristic of the substance. The ejected electrons
leaving the body with the largest normal velocity will be those that were
directly at the surface. The kinetic energy of such electrons is given by
characteristic of the substance. The ejected electrons
leaving the body with the largest normal velocity will be those that were
directly at the surface. The kinetic energy of such electrons is given by
In the body is charged to a positive potential ![]() and is surrounded by
conductors at zero potential, and if
and is surrounded by
conductors at zero potential, and if ![]() is just large
enough to prevent
loss of electricity by the body, if follows that:
is just large
enough to prevent
loss of electricity by the body, if follows that:
where
where
If one takes
![]() , then
, then
![]() is
the potential
in volts which the body assumes when irradiated in a vacuum.
is
the potential
in volts which the body assumes when irradiated in a vacuum.
In order to see whether the derived relation yields an
order of magnitude
consistent with experience, we take
![]() ,
,
![]() (corresponding to the limit of the
solar spectrum toward the ultraviolet) and
(corresponding to the limit of the
solar spectrum toward the ultraviolet) and
![]() .
We obtain
.
We obtain
![]() volts, a
result agreeing in order magnitude with those
of Herr Lenard.9
volts, a
result agreeing in order magnitude with those
of Herr Lenard.9
If the derived formula is correct, then ![]() , when represented in Cartesian
coordinates as a function of the frequency of the incident light, must be a
straight line whose slope is independent of the nature of the emitting
substance.
, when represented in Cartesian
coordinates as a function of the frequency of the incident light, must be a
straight line whose slope is independent of the nature of the emitting
substance.
As far as I can see, there is no contradiction between these conceptions and the properties of the photoelectric observed by Herr Lenard. If each energy quantum of the incident light, independently of everything else, delivers its energy of electrons, then the velocity distribution of the ejected electrons will be independent of the intensity of the incident light; on the other hand the number of electrons leaving the body will, if other conditions are kept constant, be proportional to the intensity of the incident light.10
Remarks similar to those made concerning hypothetical deviations from Stokes's Rule can be made with regard to hypothetical boundaries of validity of the law set forth above.
In the foregoing it has been assumed that the energy of at least some of the
quanta of the incident light is delivered completely to individual electrons. If
one does not make this obvious assumption, one obtains, in place of the last
equation:
For fluorescence induced by cathode rays, which is the inverse process to the
one discussed above, one obtains by analogous considerations:
In the case, of the substances investigated by Herr Lenard,
9. Concerning the Ionization of Gases by Ultraviolet Light Solid Bodies
We shall have to assume that, the ionization of a gas by ultraviolet light, an
individual light energy quantum is used for the ionization of an individual gas
molecule. From this is follows immediately that the work of ionization (i.e.,
the work theoretically needed for ionization) of a molecule cannot be greater
than the energy of an absorbed light quantum capable of producing this effect.
If one denotes by ![]() the (theoretical) work of ionization per gram equivalent,
then it follows that:
the (theoretical) work of ionization per gram equivalent,
then it follows that:
According to Lenard's measurements, however, the largest effective wavelength for air is approximately
An upper limit for the work of ionization can also be obtained from the ionization potentials of rarefied gases. according to J. Stark13 the smallest observed ionization potentials for air (at platinum anodes) is about 10 V.14 One therefore obtains
There is another consequence the experimental testing of which seems to me to be
of great importance. If every absorbed light energy quantum ionizes a molecule,
the following relation must obtain between the quantity of absorbed light ![]() and the number of gram molecules of ionized gas
and the number of gram molecules of ionized gas ![]() :
:
If our conception is correct, this relationship must be valid for all gases
which (at the relevant frequency) show no appreciable absorption without
ionization.
Received 18 March 1905
Footnotes
- ... gases.1
- This assumption is equivalent to the supposition that the average kinetic energies of gas molecules and electrons are equal to each other at thermal equilibrium. It is well known that, with the help of this assumption, Herr Drude derived a theoretical expression for the ratio of thermal and electrical conductivities of metals.
- ... derived2
- M. Planck, Ann. Phys. 1, 99 (1900).
- ... process.3
- This problem can be
formulated in the following manner. We expand the
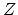 component of the
electrical force (
component of the
electrical force (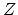 ) at an arbitrary point during the time interval between
) at an arbitrary point during the time interval between 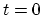 and
and 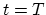 in a Fourier series in which
in a Fourier series in which
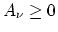 and
and
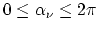 : the time
: the time 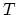 is taken to be very large relative
to all the periods of oscillation that are present:
is taken to be very large relative
to all the periods of oscillation that are present:
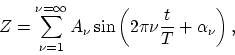
If one imagines making this expansion arbitrary often at a given point in space at randomly chosen instants of time, one will obtain various sets of values of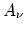 and
and 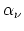 . There then exist for the frequency of occurrence of
different sets of values of
. There then exist for the frequency of occurrence of
different sets of values of 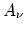 and
and 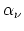 (statistical)
probabilities
(statistical)
probabilities 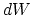 of the form:
of the form:
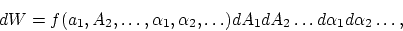
The radiation is then as disordered as conceivable if
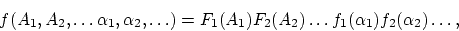
i.e., if the probability of a particular value of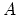 or
or 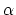 is independent of other values of
is independent of other values of 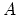 or
or 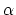 .
The more
closely this condition is fulfilled (namely, that the individual pairs of values
of
.
The more
closely this condition is fulfilled (namely, that the individual pairs of values
of 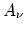 and
and 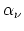 are dependent upon the emission and absorption
processes of specific groups of oscillators) the more closely will radiation in
the case being considered approximate a perfectly random state.
are dependent upon the emission and absorption
processes of specific groups of oscillators) the more closely will radiation in
the case being considered approximate a perfectly random state.
- ... formula,4
- M. Planck, Ann. Phys. 4, 561 (1901).
- ... frequencies.5
- This assumption is an arbitrary one. One will naturally cling to this simplest assumption as long as it is not controverted experiment.
- ... thermodynamically,6
- If
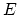 is the energy of the system,
one obtains:
is the energy of the system,
one obtains:
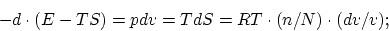
therefore
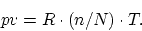
- ... paper.7
- P. Lenard, Ann. Phys., 8, 169, 170 ( 1902).
- ... body.8
- If one assumes that the individual electron is detached from a
neutral molecule by light with the performance of a certain amount of work,
nothing in the relation derived above need be changed; one can simply consider
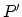 as the sum of two terms.
as the sum of two terms.
- ... Lenard.9
- P.Lenard, Ann. Phys. 8, pp. 163, 185, and Table I, Fig. 2 (1902).
- ... light.10
- P. Lenard, Ref. 9, p. 150 and p. 166-168.
- ...\space 11
- Should
be
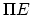 (translator's note).
(translator's note).
- ... volts.12
- P. Lenard, Ann. Phys., 12, 469 (1903).
- ... Stark13
- J. Stark, Die Electrizitët in Gasen (Leipzig, 1902, p. 57)
- ... V.14
- In the interior of gases the ionization potential for negative ions is, however, five times greater.