Secciones Destacados Trabajos

Trabajos Secciones Por rama Por nivel Por tipo Trabajos Otros

Búsqueda

Bájatelo

Isaac Newton

pod

Date: Diciembre 1993

1 Biografía

Isaac Newton; matemático, físico y astrónomo ingles, nacido en Woolsthorpe el día de navidad de 1642¹ y muerto en Londres el 1727, siendo enterrado en el pabellón de los hombres ilustres de la abadía de Westminster.

Se inmortalizó por el descubrimiento de las leyes de la mecánica y la gravitación universal, su explicación de la descomposición de la luz en los diferentes colores, y por sus nobles trabajos relativos al álgebra i la geometría, así como la invención (de forma independiente de Lebnitz) del calculo diferencial.

Otros de sus descubrimientos o invenciones importantes son:

$\bullet$

$\bullet$ obtención de los anillos de Newton (un fenómeno óptico que se produce por la refracción de la luz en materiales de grosor variable),

$\bullet$ otros fenómenos ópticos como anillos de interferencias y el disco de luz blanca,

$\bullet$ tubo de vacío par demostrar la caída de materiales,

$\bullet$ etc.

Estudió en el colegio Trinidad (trinity college) de la universidad de Cambridge. Siguiendo técnicas de su maestro Barrow, familiarizándose con la geometría de Descartes y la aritmética de Wallis, descubrió el método de las tangentes²y el calculo de fluxsiones directas e indirectas (nuestras actuales derivadas), así como el teorema del binomio que lleva su nombre. En 1665 comenzó a pensar sobre la teoría de la gravitación universal, cuando (según la leyenda) le cayó una manzana en su jardín de Woolsthorpe. En 1671 expuso su hipótesis de la composición de la luz blanca, completando de esta forma la explicación dada por Descartes a los fenómenos como el arco iris y la reflexión. En 1675 comunicó a la docta corporación su explicación de los diferentes colores de los cuerpos expuestos a la luz blanca. De la misma forma, dio a conocer la teoría de los colores producidos por la superposición de líneas finas (anillos de Newton). Fue nombrado inspector, y posteriormente director, de la Real Casa de la Moneda, en 1696 y 1699 respectivamente. Seis años mas tarde fue nombrado caballero por la reina Ana.

2 Cronología

Newton vino al mundo en una familia de pequeños propietarios de Woolsthorpe, en el condado de Lincolnshire (Inglaterra), antes de su nacimiento ya era huérfano de padre. Su infancia fue marcada por continuas enfermedades, su familia dudaba que sobreviviera muchos años. A esta temprana edad su principal afición era construir sus propios juguetes. A los tres años, su madre se casó de nuevo con un rector, dejando al joven Isaac con sus abuelos. Comenzó a estudiar en dos escuelas de Woolsthorpe, hasta q ingresó con doce años en la escuela de Grantham. No era un gran estudiante, pero un día se peleó con un compañero y decidió adelantarlo en los estudios: consiguió llegar a ser el primero en su clase.

Al rededor de los quince años, volvió a ayudar a la granja materna, por la muerte de su padrastro. Cuando iba a vender al mercado de Grantham, dejaba su trabajo al criado para leer tratados científicos, de no ser por esta picardía la ciencia se echaría a faltar uno sus principales exponentes en toda la historia. El reverendo William Ayscough, tío de Newton y diplomado por el Trinity College de Cambridge, insistió para que se matriculara en Cambridge, donde consiguió el bachillerato en matemáticas, física y geometría (se matriculó de física ya que quería entender los tratados de astrología, que en aquellos tiempos estaba mezclada con la ciencia real). Nuevamente, volvió a la granja materna, asolada por la peste, donde se dice que observó la caída de una manzana a la vez q veía la luna, cosa que le sirvió de inspiración para su famosa teoría de la gravitación universal. En un principio, no publicó sus resultados dado que no cuadraban con los datos disponibles en la época. Sin embargo, los que estaban equivocados eran los experimentales, cosa que no descubrió hasta años después.

Entre 1656 y 1666 enfocó sus investigaciones a la óptica. Hizo pasar la luz por un pequeño orificio hacia una habitación oscura. Hizo atravesar el haz por un prisma de caras no paralelas, obteniendo una figura similar al arco iris: había demostrado que la luz blanca está compuesta por todos los colores del arco iris. Otro descubrimiento importante en esta época es el telescopio de reflexión axial. Estos descubrimientos fueron compendiados en su primer libro importante, el óptica.

En 1666 aporta a las matemáticas el calculo infinitesimal (que el llamaba cálculo de fluxiones), con la cual cosa se puso al frente de las matemáticas contemporáneas. Este año fue el llamado año milagroso, ya que además de todos estos los descubrimientos ya enumerados realizó la primera formulación de las leyes de la mecánica.

Años posteriores fueron marcados por mejoras intensivas de las técnicas que había ido desarrollando, y culminaron con la publicación el verano de 1687 del libro de ciencia posiblemente más conocido de la historia, los Philosophiae naturalis principia mathematíca (los Principia), donde daba a conocer sus tres leyes para la dinámica, que se pueden resumir de la forma

$\bullet$

$\bullet$ Segunda ley de Newton: Establece que la aceleración sufrida por un cuerpo es proporcional a la resultantes de las fuerzas sobre él aplicadas, siendo la constante de proporcionalidad el recíproco de la masa, $\vec{F} = m \vec{a}$ . Esta ley establece la primera diferencia entre la masa (cantidad de inercia) y su peso (cantidad de fuerza gravitatoria entre dos cuerpos).

$\bullet$ Principio de acción y reacción: Señala que toda fuerza que un cuerpo aplica sobre un segundo siempre va acompañada de una fuerza de igual intensidad, dirección y línea de acción, pero de sentido contrario, que el segundo cuerpo aplica sobre el primero. Este principio es equivalente al principio de conservación de la cantidad de movimiento.

Además, publicaba una relación matemática entre la fuerza gravitatoria entre dos cuerpos en el espació. Postulaba que dicha fuerza debe ser directamente proporcional al producto de cada masa e inversamente proporcional al cuadrado de la distancia entre ambos³. Además, la fuerza siempre es atractiva y en la línea que une ambos cuerpos. Esta proporcionalidad se convierte en una igualdad introduciendo la constante de la gravitación universal, G, de forma que podemos escribir de la forma

$\displaystyle F = G \frac{m_1 m_2}{r^2} \hat{r} ,$

esta es la famosa ley de la gravitación universal. A partir de esta ecuación, pudo deducir matemática mente las órbitas elípticas de Kepler (el matemático errante).

La publicación de los «Principia» le conllevó algunas polémicas; Hooke (que ya lo había molestado cuando se publicó el «óptica») le acusó de plagio, cosa que hoy en día pocos historiadores creen posible. A la muerte de Hooke, el 1703, Newton se burló de su baja estatura con la conocida frase «si he visto más lejos es por que me he subido a hombros de gigantes» (que hoy en día figura en las monedas inglesas). Además, se jactó de haber «roto el corazón» de Hooke. Halley apoyó a Newton, aportando dados experimentales que confirmaban las predicciones de la teoría de Newton.

En 1693, hace 310 años, su perro, llamado Diamante, hizo caer una vela sobre unos manuscritos imposibles de rehacer, cosa que lo hizo caer en una depresión que le conllevó graves problemas psicológicos, de los que finalmente pudo salir airoso. En 1699 fue elegido director de la Casa de la Moneda, como premio a su buen hacer como guardián de dicho instituto.

En 1705 la reina Ana de Inglaterra lo nombró caballero, Sir Isaac Newton, y fue invitado a participar en las sesiones de la cámara de los Lores del parlamento británico. La leyenda cuenta que tan solo pidió la palabra una vez en varios años, cosa que causó gran espectador entre el resto de parlamentarios. Sus palabras fueron algo similar a «¿pueden cerrar la ventana? tengo algo de frío!».

En sus últimos años sufrió una piedra en la vesícula, que lo llevó a la muerte el veinte de marzo de 1727. Parece ser que no sufrió demasiado, hasta el último día hizo vida normal. Hoy en día descansa en la abadía de los hombre míticos de Westminster. El epitafio que reza en su tumba, redactado por Fatio, es el siguiente:

«Felicitaros los mortales que tal y tan grande
adorno del género humano haya existido.»

3 Los descubrimientos, inventos, etc.

3.1 Lista

A continuación mostramos una lista de los principales descubrimientos e inventos que Newton aportó a la historia de la ciencia. Algunos de ellos, los marcados con un asterisco, serán ampliados en apartados posteriores.

$\bullet$ Fuerza centrípeta: Del latín hacia el centro, es la fuerza resultante que causa de todo movimiento circular, dirigida hacia el centro y con una magnitud igual a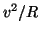

, siendo

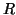el radio de la circunferencia instantánea que describe la trayectoria. Esta ley, aplicada al movimiento de la luna, pudo ser la inspiración a la ley del cuadrado de la distancia de la gravitación universal.

$\bullet$ Descomposición de la luz en colores:* Explicó el fenómeno mediante una teoría corpuscular de a descomposición de la luz blanca en los diferentes colores del arco iris en pasar por prismas transparentes.

$\bullet$ Gravitación universal:* Cuantificó y describió la atracción de los cuerpos por el simple hecho de tener masa.

$\bullet$ Leyes de Kepler: Las demostró matemáticamente a partir de su teoría de la gravitación universal. Las leyes de Kepler sobre las órbitas de los planetas afirman que: 1.- las órbitas son elípticas, con el sol en un foco de la misma; 2.- el radio vector que une el planeta con el sol barre áreas iguales en tiempos iguales; 3.- el cubo del semieje mayor de la elipse orbital de cada planeta es proporcional al cuadrado del período que tarda el planeta.

$\bullet$ Hipótesis corpuscular de la luz: Intentó explicar diversos aspectos de la propagación de la luz suponiendo que estaba formada por pequeños proyectiles, corpúsculos. Ésta fue la teoría dominante hasta los experimentos de doble rendija de Young.

$\bullet$ Mecánica newtoniana:* La mecánica es l parte de la física que se encarga de estudiar el movimiento de los cuerpos y sus causas. La formulación newtoniana es la más sencilla y práctica en la mayoría de situaciones en que no intervienen correcciones relativistas y cuánticas.

$\bullet$ Óptica: Hizo diferentes adelantos en óptica, entre los que destaca el telescopio de reflexión. Probablemente el «Óptica» sea el segundo libro en importancia que publicó a lo largo de su vida.

$\bullet$ Leyes del movimiento:* Las tres leyes que fundamentan la mecánica de Newton fueron publicadas en su libro más importante, los «Principia».

3.2 Mecánica

La mecánica física (estudio del movimiento de la materia en el espacio, y de sus causas) tiene millones de años de antigüedad, aunque los adelantos más importantes no se produjeron hasta a época de Newton.

El concepto del movimiento anterior a Newton, procedente de los antiguos griegos, dependía de la creencia sobre que la tierra era el centro inamovible y fijo del universo. Los objetos tendían a situarse en su nivel natural: tierra, agua, aire y fuego.

Igualmente, el desarrollo de la mecánica newtoniana tiende a comprender la definición y el análisis del movimiento, teniendo en cuenta que las deducciones han de ser aplicadas también en la astronomía para la descripción del movimiento de planetas y astros. Ésto, por primera vez, unifica la física de lo terrestre y lo celestial.

Newton descompuso el movimiento de los cuerpos en dos contribuciones: el movimiento natural y el artificial. El movimiento natural es aquél causado por la gravedad, que tiende a hacer que los objetos se acerquen mutuamente. El movimiento artificial es aquél que está causado por la aplicación de otras fuerzas en el presente o en instantes pasados. El resultado es una línea curvada que puede calcularse a partir de la aplicación de las leyes de la mecánica de Newton.

Newton demostró empíricamente la hipótesi de Galileo sobre la caída de cuerpos en un tubo de vacío, en que la caída de los mismos (el movimiento natural de la materia) es independiente de la masa.

3.3 Teoría de la luz

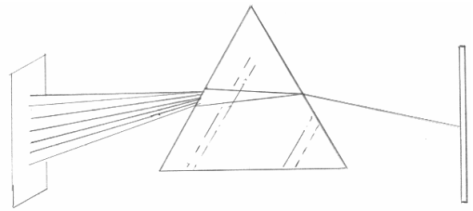
Newton realizó el conocido experimento de doble refracción mediante prismas de vidrio transparente con caras no paralelas. En una primera etapa, el experimento se realiza con tan solo un prisma. Un haz de luz blanca que entra a un cuarto oscuro traviesa un trozo de cristal con caras planas no paralelas y sufre una doble refracción al entrar y salir del mismo. La luz se recoge con una pantalla. El resultado que se obtiene es un haz que contiene todos los colores naturales separados: el rojo, naranja, amarillo, verde, azul, añil y violeta. Ésto se puede ver en la figura 1.

**Figura 1:** Refracción y descomposición de la luz en un prisma de caras no paralelas.

Newton no creía en las afirmaciones de sus coetáneos sobre este fenómeno, que interpretaban que el color se formaba en el prisma, sino que supuso que la luz blanca era una mezcla de haces de los siete colores puros. Cada uno de estos haces posee un grado propio y diferente de refracción en el vidrio. Esta hipótesis también explica la formación del propio arco iris, ya que la luz que se refracta en las gotas de lluvia puede separarse de una forma parecida a la que hemos observado en la figura 1. Para intentar demostrar esta hipótesis, Newton realizó dos experimentos más.

El primer experimento consiste en añadir un segundo prisma, invertido respecto al primero, de forma que el haz de luz se vuelve a reunir para formar de nuevo un haz blanco, tal y como vemos en la figura 2.

**Figura 2:** La luz descompuesta en el primer prisma se vuelve a reunir para formar un nuevo haz blanco.
$\includegraphics[width=16cm]{dosprimes}$

El segundo experimento es el disco de Newton, una ruleta que esta dividida en siete sectores, cada cual pintado con uno de los colores del arco iris. Al hacerlo girar a gran velocidad, la apariencia del disco es blanca.

Posteriormente, Newton quiso encontrar la explicación a la aparición de colores en los diferentes objetos cuando son iluminados por luz blanca. Cada substancia, argumentaba, posee una capacidad selectiva de absorción de cada color diferente. La parte no absorbida de la luz blanca es la única que llega a nuestros ojos, que la interpretan como si fuera una única luz con el color resultante de la combinación de las diferentes contribuciones de cada color natural.

Newton intentó demostrar esta explicación mediante un dispositivo experimental del tipo de la figura 2. Mediante una pantalla opaca con una ranura apropiada, se bloquean seis de los siete colores en los cuales se ha separado la luz al pasar por el primer prisma, dejando pasar tan solo uno de ellos. La luz restante pasa por el segundo prisma sin modificarse en absoluto, ya que en este caso tan sólo resta una de las componentes: el haz es homogéneo. Los objetos iluminados con esta luz serán negros si absorben este color en particular, o de ese mismo color en caso contrario. De esta forma, Newton demostró que el color de cada objeto depende de la iluminación y de la capacidad de absorción de cada color.

3.4 Gravitación universal

En la caída de los cuerpos en arco, según la primera ley de Newton, debe existir una fuerza diferente de cero, ya que sino el cuerpo seguiría una trayectoria rectilínea. Esta fuerza se ha dado a llamar gravedad. Su dirección está en la linea que une los centros de masas de cada cuerpo, y su sentido siempre es atractivo. Newton propuso una pequeña pero revolucionaria idea: que la fuerza que actúa en la caída de los cuerpos en la tierra, y la que crea las órbitas elípticas de los planetas, tienen el mismo origen. Supongamos que estamos en la cima de una gran montaña y que lanzamos un proyectil de forma horizontal. Éste seguirá una trayectoria curva hacia el suelo. Si lanzamos otro proyectil más largo, la curva que describirá será más amplia. Y así sucesivamente, hasta que lancemos el proyectil tan rápidamente que, debido a la curvatura de la tierra, no llegue a chocar contra el suelo y vuelva a nosotros por detrás tras haber dado la vuelta al mundo (hoy en día, la trayectoria de los satélites artificiales se pueden explicar de esta forma). En resumen, el movimiento del proyectil seria una curva cerrada al rededor de la tierra, muy similar a la que describen los planetas en rededor del sol.

Tan solo resta, pues, describir las condiciones en que se produce la atracción gravitatoria en el marco de la teoría de Newton. Según el teorema de Gauss, todos los cuerpos con simetría esférica (la mayoría) se atraen unos a otros como si toda su masa estuviera concentrada en el centro. Además, por el tercer principio de Newton, el de acción y reacción, la atracción debe ser mutua.

Siendo la gravitación una propiedad de la masa, es lógico pensar que la atracción crecerá proporcionalmente con la masa de ambos cuerpos involucrados, es decir, la fuerza gravitatoria debe ser proporcional al producto de las masas de los dos cuerpos.

Para explicar la proporcionalidad inversa con el cuadrado de la distancia. Podemos imaginar que la gravedad se expande en todas direcciones e el espacio de igual forma. Por tanto, podemos considerar que la fuerza se distribuye uniformemente por la superficie de una esfera de radio . La intensidad de la fuerza sera mayor cuanto menor sea la superficie de dicha esfera, ya que al suponer difusión uniforme la fuerza sera inversamente proporcional a la superficie. Dado que la superficie de una esfera se escribe de la forma $S = 4 \pi r^2$ , que crece de forma proporcional al cuadrado de la distancia, la fuerza decrecerá de forma inversamente proporcional a .

Así pues, siguiendo estos razonamientos, u otros equivalentes, Newton llegó a establecer que la fuerza debida a la gravedad entre dos masas, de valores y , separadas una distancia cumple la ecuación,

$\displaystyle F \propto \frac{m_1 m_2}{d^2} ,$

donde el signo $\propto$ indica proporcionalidad. Podemos transformar la proporcionalidad a una igualdad introduciendo la constante de la gravitación universal, G, de la forma,

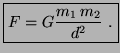
$\displaystyle \boxed{F = G\frac{m_1 m_2}{d^2} .}$

De hecho, el valor de la constante de la gravitación universal no se supo hasta más de medio siglo después de la muerte de Newton. El primero en medirlo fue el excéntrico físico británico Henry Cavendish (1731-1810), que obtuvo el valor

$\displaystyle G = 6,7 \cdot 10^{-11} \mathrm{N \cdot m^2 kg^{-2}} .$

3.5 Teoría del movimiento de Newton

La aceleración, la velocidad y la posición son cantidades vectoriales, es decir, para especificarlas completamente necesitamos indicar una dirección y sentido al mismo tiempo que la magnitud. Por ejemplo, en el movimiento circular uniforme, la velocidad y la aceleración son siempre perpendiculares: la aceleración, de valor

, siempre apunta hacia el centro de la trayectoria, mientras que la velocidad es tangente a la misma.

Los conceptos básico de las leyes del movimientos descritas en la obra magna de Isaac Newton son:

$\bullet$ Masa: la cantidad de materia que contiene un cuerpo, que mide la oposición de un cuerpo a cambiar su estado de movimiento.

$\bullet$ Cantidad de movimiento: en la mecánica newtoniana la cantidad de movimiento se define como el producto de la masa por la velocidad.

$\bullet$ Inercia: la inercia es la propiedad de los cuerpos con masa de oponerse al cambio en su estado de movimiento, es decir, la oposición que presentan a sufrir aceleración bajo influencia de una fuerza.

$\bullet$ Fuerza: es la acción que un cuerpo ejerce sobre otro produciendo uno de los siguientes efectos: cambiar el valor de la velocidad del cuerpo, desviarlo de su trayectoria inicial, producir una deformación o bien cancelar fuerzas producidas por otros cuerpos.

La forma en que la aplicación de una fuerza afecta a los valores de las otras propiedades del movimiento del cuerpo se resumen en las tres leyes de Newton de la mecánica.

$\bullet$ Primera ley de Newton: Si no ejercemos ninguna fuerza sobre un cuerpo, si este esta en reposo tiende a mantenerse en reposo, y si su movimiento es rectilíneo uniforme, permanece de esta forma indefinidamente. Esta ley significó un cambio radical respecto las antiguas creencias aristotélicas del movimiento, que aseguraban que todo movimiento tenia una causa, mientras que Isaac aseguraba que el hecho de mantener el estado de movimiento es lo habitual, y tan solo los cambios en el estado de movimiento están relacionados con la existencia de una acción sobre el cuerpo. Además, el principio de inercia hizo abandonar la teoría del lugar natural que hemos comentado anteriormente.

$\bullet$ Segunda ley de Newton: El cambio instantáneo en cantidad de movimiento es igual a la fuerza motriz impresa, y se efectúa en la misma dirección de la línea recta en que se imprime dicha fuerza. Esta segunda ley se puede expresar de forma matemática mediante, tal vez, la formula más conocida de la física,

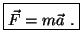
$\displaystyle \boxed{ \vec{F} = m \vec{a} . }$

$\bullet$ Tercera ley de Newton: Cualquier acción efectuada sobre un cuerpo por parte de un segundo, siempre hay una reacción de la misma magnitud y línea de aplicación, pero de sentido opuesto, que el segundo cuerpo efectúa sobre el primero. En el marco de la teoría newtoniana, la acción (o reacción) entre dos cuerpos es recíproca e instantánea, es decir, diferenciación entre acción y reacción es artificial. Además, se pueden producir por contacto (fuerzas de rozamiento) o a distancia (gravitación).

Bibliografía

1: 12000 Grandes, Enciclopedia Universal, páginas 149-154.
Promesca.
2: Diccionario Español, página 960.
Vox.
3: Enciclopedia universal sopena, página 960.
Ed. Sopena, 1985.

Notas al pie

... 1642 ¹

Esta fecha corresponde al calendario juliano vigente en el reino unido en aquella época. En el calendario gregoriano usado en la actualidad dicha fecha corresponde al 4 de Enero de 1643.

... tangentes ²

El método de las tangentes, o de Newton-Raphson, nos permite mejorar sucesivamente una aproximación a la solución de la ecuación

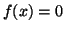. En cada iteración se obtiene un valor 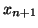$x_{n+1}$ que se obtiene del anterior

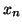según la ecuación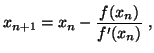

$\displaystyle x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} ,$

que, según ciertas condiciones, mejora la aproximación anterior.

... ambos ³

Si los cuerpos son extensos, se considera el centro de masas de los mismos

Acceso rápido