Ecuaciones de Einstein

pod


Date: Octubre 2004

1 Introducción

Las ecuaciones de Einstein constituyen la base del aparato predictivo de la Relatividad General. De ellas se puede obtener cual es el efecto de la materia sobre la geometría del espacio, y viceversa. La relatividad general se basa en la maquinária matemática de las geometría diferencial de las variedades métricas. Así, pues, para formular las ecuaciones de Einstein, necesitamos recordar algunos de los conceptos de la geometria diferencial en variedades métricas. Todos los índices en las ecuaciones de este documento toman valores de 0 a 3 (considerando un espacio-tiempo de 4 dimensiones, siendo el tiempo la dimensión 0-ésima).

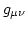Métrica, $ g_{\mu\nu}$ :
Describe cual es la distancia espacio-temporal entro dos sucesos infinitesimalmente juntos.

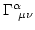Símbolos de Chistoffeld, $ \Gamma^\alpha_{ \mu\nu}$ :
Describen la variación de los vectores de una base 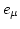$ e_\mu$ . Es decir, la derivada covariante del vector de la base 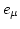$ e_\mu$ a lo largo del vector de la base 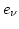$ e_\nu$ es un nuevo vector de componentes 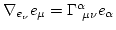$ \nabla_{e_\nu} e_\mu = \Gamma^\alpha_{\ \mu\nu} e_{\alpha}$ . En una variedad con una métrica definida, los símbolos de Chistoffeld se determinan completamente a partir de la métrica,

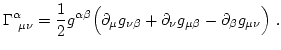
$\displaystyle \Gamma^\alpha_{ \mu\nu} = \frac12 g^{\alpha\beta} \Big( \partial... ... g_{\nu\beta} + \partial_\nu g_{\mu\beta} - \partial_\beta g_{\mu\nu} \Big) .$ (1)

Curva geodésica:
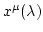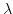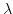Una curva geodésica, $ x^\mu(\lambda)$ , es aquella curva que une cualquiera de sus dos puntos con una distancia espacio-temporal estacionaria. Se puede determinar, para cierto parámetro $ \lambda$ , mediante la siguiente ecuación diferencial (donde los puntos indican derivación parcial respecto $ \lambda$ )

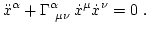
$\displaystyle \ddot x^\alpha+ \Gamma^\alpha_{\ \mu\nu} \, \dot x^\mu \dot x^\nu = 0 \ .$ (2)

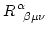Tensor de Riemman, $ {R }^\alpha_{ \beta\mu\nu}$ :
Describe la curvatura de la variedad métrica, es decir, da el grado de desviación relativo de dos curvas geodésicas proximas. Se determina enteramente a partir de los símbolos de Christoffeld,

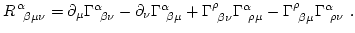
$\displaystyle {R }^\alpha_{ \beta\mu\nu} = \partial_\mu \Gamma^\alpha_{ \bet... ...mma^\alpha_{ \rho\mu} - \Gamma^\rho_{ \beta\mu} \Gamma^\alpha_{ \rho\nu} .$ (3)

Tensor y escalar de Ricci:
Se definen como las diferentes contracciones del tensor de Riemman,

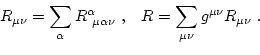
\begin{equation*}\begin{aligned}R_{\mu\nu} & = \sum_\alpha R^{\alpha}_{ \mu\alp... ... , & R & = \sum_{\mu\nu} g^{\mu\nu} R_{\mu\nu} . \end{aligned}\end{equation*}

2 Formulación de las ecuaciones de Einstein

Las ecuaciones de Einstein determinan las características de la variedad métrica, nuestro espacio-tiempo, a partir de la distribución de masa y energía que puebla el espacio. Dicha distribución de masa y energía viene descrito por el tensor de energía-impulso, $ T_{\mu\nu}$ , que se define como la densidad de la componente $ \mu$ -ésima del cuadrimomento que atraviessa una hipersuperfície $ x^\nu$ constante.

Las ecuaciones de Einstein tienen la siguiente forma:

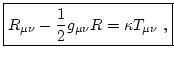$\displaystyle \boxed{ R_{\mu\nu} - \frac12 g_{\mu\nu} R = \kappa T_{\mu\nu} , }$ (5)

donde $ \kappa = 8 \pi G$ , siendo G la constante de la gravitacion universal de Cavendish. A veces, el término izquierdo de las ecuaciones de Einstein se resume definiendo el tensor de Einstein, $ G_{\mu\nu} = R_{\mu\nu} - \frac12 g_{\mu\nu} R$ .

3 Comentarios adicionales

Dado que todos los tensores que aparecen en las Ecuaciones de Einstein son simétricos, tenemos tan sólo diez ecuaciones de Einstein. Cuatro de ellas, las que tienen $ \mu=0$ , no son ecuaciones dinámicas, por lo que tan sólo nos quedan seis ecuaciones dinámicas a resolver.

Dichas ecuaciones determinan como la distribución de masa y energía (descrita por $ T_{\mu\nu}$ ) afectan a la geometría del espacio-tiempo (descrita por $ G_{\mu\nu}$ que, en último término, depende únicamente de la métrica). Y viceversa, determinan como la geometría del espacio-tiempo afecta al movimiento de la masa y energía distribuida por el mismo. Las partículas puntuales se mueven siguiendo las curvas geodésicas que, como hemos vistos, se determinan directamente a partir de la geometría del espacio-tiempo.

4 Constante cosmológica

Para algunas aplicaciones cosmológicas, es común añadir un término más a las ecuaciones de Einstein,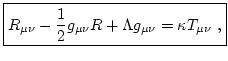

$\displaystyle \boxed{ R_{\mu\nu} - \frac12 g_{\mu\nu} R + \Lambda g_{\mu\nu} = \kappa T_{\mu\nu} , }$ (6)

donde $ \Lambda$ es la llamada constante cosmológica. En la actualidad, dicho término se interpreta como la desnidad de energía del vacío por lo que, de hecho, actualmente se considera como un término más dentro del tensor de energía-impulso.

5 Rango de validez

Para la mayor parte de las aplicaciones de la física en situaciones cotidianas no es necesario recurrir a la relatividad general, y por tanto a las ecuaciones de Einstein, ya que la aproximación de la física Newtoniana es suficiente. La aproximación Newtoniana es válida si, en cierta forma, el campo gravitatorio es suficientemente débil para que la velocidad de escape sea mucho menor que la velocidad de la luz, es decir, si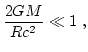

$\displaystyle \dfrac{2G M}{R c^2} \ll 1 ,$ (7)

donde $ M$ es la masa del objeto que crea el campo gravitatorio, y $ R$ la distáncia a su centro de masas.

Por otra parte, la relatividad general tiene soluciones con puntos singulares, como la métrica de Schwarchild que describe los agujeros negros esféricos, o como la singularidad inicial del big bang. En la cercania de dichas singularidades, la relatividad general no es válida: necesita ser reemplazada por una teoría más avanzada, que aún no conocemos (la Teoría de Cuerdas es el candidato mejor situado).

Además, tampoco es posible aplicar la relatividad general en aquellas situaciones donde son importante los efectos cuánticos, como por ejemplo situaciones donde intervengan distáncias muy pequeñas o energías muy altas. Este límite de la teoría, de hecho, está muy relacionado con el anterior, y de nuevo la Teoría de Cuerdas es nuestro más firme candidato para solucionar estos problemas.