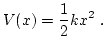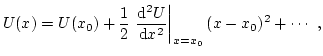Oscilador armónico

pod


Date: Octubre 2004

1 Introducción

El oscilador armónico es uno de los sistemas más estudiados en la física, ya que todo sistema que oscila al rededor de un punto de equilibrio estable se puede estudiar en primera aproximación como si fuera un oscilador.

La característica principal de un oscilador armónico es que está sometido a una fuerza recuperadora, que tiende a devolverlo al punto de equilibrio estable, con una intensidad proporcional a la separación respecto de dicho punto,

$\displaystyle F = - k ( x - x_0 ) \ ,$ (1)

donde k es la constante de recuperación, y $ x_0$ es la posición de equilibrio, que sin pérdida de generalidad podemos tomar $ x_0 = 0$ .

La fuerza recuperadora es conservativa, por lo que tiene asociado una energía potencial,

$\displaystyle V(x) = \frac12 k x^2 \ .$ (2)

2 Casos relevantes

2.1 Oscilador armónico simple

El oscilador armónico simple es el caso más sencillo, donde únicamente se considera la fuerza recuperadora. Teniendo en cuenta que $ F = m a = m \frac{\mathrm{d}^2 x}{\mathrm{d}t^2}$ , la ecuación (1) nos da la siguiente ecuación diferencial

$\displaystyle \boxed{\ddot{x} + \omega_0^2 x = 0 \ ,}$ (3)

donde los puntos indican derivación respecto del tiempo, y $ \omega_0^2 = \sqrt{k/m}$ es la frecuencia natural de vibración. La solución general a esta ecuación se puede escribir de la forma

$\displaystyle x(t) = A \sin \left( \omega_o t + \varphi_0 \right) \ ,$ (4)

donde A y $ \varphi_0$ se obtienen imponiendo las condiciones iniciales.

2.2 Oscilador armónico amortiguado

Este caso más realista consiste en tener en cuenta el rozamiento del aire, que tiende a amortiguar la oscilación. El modelo más usual consiste en tomar un rozamiento proporcional a la velocidad,

$\displaystyle F_r = - b \dot{x} \ ,$ (5)

con lo que la ecuación diferencial, obtenida a partir de la segunda ley de Newton, queda de la forma

$\displaystyle \boxed{ \ddot{x} + 2 \gamma \dot{x} + \omega_0^2 x = 0 \ , }$ (6)

donde $ \gamma = b/2m$ . La solución general a esta ecuación depende de la relación entre $ \gamma$ y $ \omega_0$ . Tenemos tres casos:
Oscilador infraamortiguado:
Este es el caso 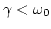$ \gamma < \omega_0$ . La solución es de la forma

$\displaystyle x(t) = A \, \mathrm{e}^{- \gamma t} \sin\left( \omega_1 t + \varphi_0 \right) \ ,$ (7)

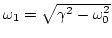donde $ \omega_1 = \sqrt{\gamma^2 - \omega_0^2}$ .

Oscilador crítico:
En este caso 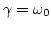$ \gamma = \omega_0$ . La solución general es

$\displaystyle x(t) = \big( A + B t \big) \, \mathrm{e}^{-\gamma t} \ .$ (8)

Oscilador sobreamortiguado:
Por último, tenemos el caso 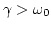$ \gamma > \omega_0$ . La nueva solución general es

$\displaystyle x(t) = A \mathrm{e}^{-\gamma t} \sinh\left(\omega_1 t + \varphi_0 \right) \ ,$ (9)

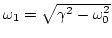donde $ \omega_1 = \sqrt{\gamma^2 - \omega_0^2}$ .

2.3 Oscilador simple forzado

Decimos que un oscilador está forzado si sobre él se aplica una fuerza externa. El caso más interesante es cuando la fuerza de forzamiento es también periódica, por ejemplo sinuosidal,

$\displaystyle F_$for$\displaystyle = f_0 \cos \omega t \ .$ (10)

Esta fuerza se convierte en un término inhomogéneo en la ecuación diferencial del movimiento

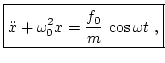$\displaystyle \boxed{ \ddot{x} + \omega^2_0 x = \frac{f_0}{m} \, \cos\omega t \ , }$ (11)

y la solución general es de la forma

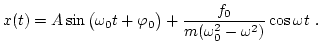$\displaystyle x(t) = A \sin\big( \omega_0 t + \varphi_0 \big) + \frac{f_0}{m (\omega_0^2-\omega^2)} \cos\omega t \ .$ (12)

2.4 Oscilador simple resonante

Como vemos, la solución anterior, ec. (12), es singular en el caso que la fuerza de forzamiento tenga la misma frecuencia que la frecuencia natural del oscilador. En este caso, tenemos un oscilador simple resonante, cuya solución es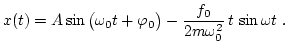

$\displaystyle x(t) = A \sin\big( \omega_0 t + \varphi_0 \big) - \frac{f_0}{2m \omega_0^2} \, t\, \sin\omega t \ .$ (13)

En este caso, obtenemos una solución secular, es decir, cuya amplitud aumenta en el tiempo hasta hacerse muy grande. Físicamente, esta solución no tiene sentido, ya que tarde o temprano el rozamiento, que siempre existe pero que en este caso despreciamos, entrará en juego impidiendo que la amplitud de oscilación crezca indefinidamente.

2.5 Oscilador amortiguado y forzado

En este caso más general incluimos una fuerza de forzamiento del tipo (10) a un oscilador amortiguado. La ecuación diferencial completa es, pues,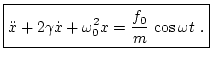

$\displaystyle \boxed{ \ddot{x} + 2 \gamma \dot{x} + \omega^2_0 x = \frac{f_0}{m} \, \cos\omega t \ . }$ (14)

En este caso, la solución general es de la forma

$\displaystyle x(t) = x_$hom$\displaystyle (t) + A_p \cos\big( \omega t + \alpha \big) \ ,$ (15)

donde $ x_$hom$ (t)$ es la solución general del oscilador sin forzar, dada por las ecuaciones (7)-(9) según la relación entre $ \gamma$ y $ \omega_0$ , y además

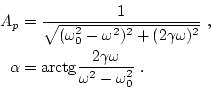\begin{equation*}\begin{aligned}A_p & = \dfrac{1}{ \sqrt{(\omega_0^2-\omega^2)^2... ...ctg} \dfrac{2\gamma\omega}{\omega^2-\omega^2_0} \ . \end{aligned}\end{equation*}

Como vemos, la solución particular, proporcional a $ A_p$ , es la única que importa para tiempos grandes, ya que todas las soluciones de la ecuación homogénea decaen exponencialmente. Así, pues, tenemos un estado estacionario, correspondiente a oscilaciones de amplitud $ A_p$ .

En este caso, la solución es válida para todas las frecuencias de la fuerza de forzamiento. Sin embargo, vemos que la amplitud de respuesta es máxima para una frecuencia: la frecuencia de resonancia,

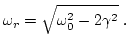$\displaystyle \omega_r = \sqrt{\omega_0^2-2\gamma^2} \ .$ (17)

3 Aplicaciones

Muchos sistemas pueden estudiarse a partir del oscilador armónico: los muelles, los péndulos (en la aproximación de ángulos pequeños), etc.

En general, cualquier sistema que oscila al rededor de un punto de equilibrio estable puede estudiarse, en primera aproximación, a partir del oscilador armónico. Esto se hace evidente si se desarrolla por Taylor la energía potencial al rededor del punto de equilibrio estable,

$\displaystyle U(x) = U(x_0) + \frac12 \left. \dfrac{\mathrm{d}^2 U}{\mathrm{d}x^2} \right\vert _{x=x_0} ( x - x_0)^2 + \cdots \ ,$ (18)

donde no hay término con derivada primera debido a que estamos en un punto de equilibrio, $ \frac{\mathrm{d}U}{\mathrm{d}x} = 0$ . Comparando este desarrollo con la ecuación (2), podemos realizar la identificación

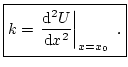$\displaystyle \boxed{ k = \left. \dfrac{\mathrm{d}^2 U}{\mathrm{d}x^2} \right\vert _{x=x_0} \ . }$ (19)

Al ser un punto de equilibrio estable, la derivada es positiva, $ k > 0$ , y por lo tanto la fuerza (1) tiende a restituir la posición de equilibrio.

4 Régimen de aplicabilidad

En primer lugar, todas las ecuaciones obtenidas no son más que casos particulares de la Segunda ley de Newton, y por lo tanto, todas las consideraciones de aplicabilidad de la segunda ley de newton son, a la vez, aplicables a este caso.

Por otra parte, como vemos de la ecuación , el oscilador armónico no es más que la aproximación de quedarse tan solo con el término de segundo orden en el desarrollo de Taylor, por lo que los resultados obtenidos serán válidos si no suponen desplazamientos del equilibrio demasiado grandes, de forma que sea una buena aproximación no tomar en consideración términos de orden superior.

Por último, debemos tener en cuenta que, para los casos con amortiguamiento, tomar la fuerza como proporcional a la velocidad es, de nuevo, una aproximación. En este caso, la expresión del rozamiento viscoso es difícil de obtener, y una aproximación como la que utilizamos suele ser útil, tan solo, en régimen laminar, lo que se suele traducir en pedir que la velocidad de la oscilación no sea excesivamente alta.