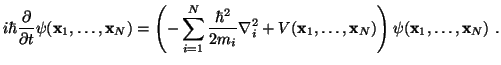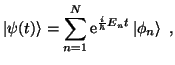Ecuación de Schrödinger

pod


Date: Mayo 2003

1 Formulaciones de la ecuación

1.1 Ecuación de Schrödinger dependiente del tiempo

La ecuación de Schrödinger, en su forma más general, indica la variación que sufre un estado física,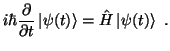 $ \ket{\psi(t)}$ a lo largo del tiempo, cuando el sistema que describe se encuentra sometido a un hamiltoniano de la forma $ \hat H$ . En estas condiciones, la ecuación de Schrödinger se escribe de la forma

$\displaystyle i \hbar \dfrac{\partial}{\partial t} \ket{\psi(t)} = \hat H \ket{\psi(t)} .$ (1)

En la mayor parte de las ocasiones, el hamiltoniano puede escribirse como suma de los operadores de energía cinética y de energía potencial. Además, normalmente se puede descomponer el operador de energía cinética como la suma de la energía cinética de cada partícula, que suele poderse escribir en función del momento lineal (de igual forma que en mecánica cuántica),

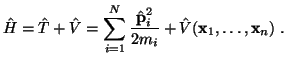$\displaystyle \hat H = \hat T + \hat V = \sum_{i=1}^N \frac{\hat {\bf p}_i^2}{2 m_i} + \hat V({\bf x}_1,\ldots,{\bf x}_n) .$ (2)

Es también común escribir la ecuación de Schrödinger en base de posiciones. En esta base, se define la función de onda $ \psi({\bf x}_1,\ldots,{\bf x}_N;t) = \left\vert \braket{ {\bf x}_1, \ldots, {\bf x}_2 \vert \psi(t) } \right\vert^2$ , que está relacionada con la probabilidad de que en el tiempo $ t$ se encuentre la primera partícula en la posición $ {\bf x}_1$ , la segunda en $ {\bf x}_2$ , etc. Además, el operador momento se puede escribir como una derivada espacial, es decir $ {\bf p}_i = - i\hbar {\bf\nabla}_i$ . Así, pues, la ecuación de Schrödinger toma la forma de una ecuación diferencial en derivadas parciales

$\displaystyle i\hbar \frac{\partial}{\partial t} \psi({\bf x}_1,\ldots,{\bf x}_... ...^2 + V({\bf x}_1,\ldots,{\bf x}_N) \right) \psi({\bf x}_1,\ldots,{\bf x}_N) .$ (3)

La forma en que Erwin Schrödinger derivó su ecuación, partiendo de una analogía entre las ecuaciones de Hamilton-Jacobi y la óptica geométrica, es la versión para una sola partícula, que se escribe de la forma

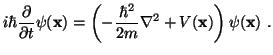$\displaystyle i\hbar \frac{\partial}{\partial t} \psi({\bf x}) = \left( - \frac{\hbar^2}{2m} {\bf\nabla}^2 + V({\bf x}) \right) \psi({\bf x}) .$ (4)

1.2 Ecuación de Schrödinger independiente del tiempo

En los casos en que el hamiltoniano es independiente del tiempo, el estado puede descomponerse en una combinación lineal de los estados propios del hamiltoniano,

$\displaystyle \ket{\psi(t)} = \sum_{n=1}^N \mathrm{e}^{\frac{i}{\hbar} E_n t} \ket{\phi_n} ,$ (5)

donde $ \ket{\phi_n}$ es el estado propio del hamiltoniano (o estado estacionario) con energía $ E_n$ , que son solución de la ecuación de Schrödinger independiente del tiempo, que en general se escribe de la forma

$\displaystyle \hat H \ket{\phi_n} = E_n \ket{\phi_n} ,$ (6)

o bien, en la base de posiciones

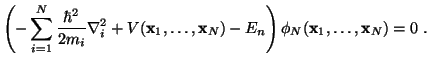$\displaystyle \left( - \sum_{i=1}^N \frac{\hbar^2}{2m_i} {\bf\nabla}_i^2 + V({\bf x}_1,\ldots,{\bf x}_N) - E_n \right) \phi_N({\bf x}_1,\ldots,{\bf x}_N) = 0 .$ (7)

Como podemos ver, esta segunda ecuación es equivalente a haber introducido la separación de variables

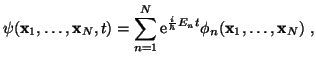$\displaystyle \psi({\bf x}_1,\ldots,{\bf x}_N, t) = \sum_{n=1}^N \mathrm{e}^{\frac{i}{\hbar} E_n t} \phi_n({\bf x}_1,\ldots,{\bf x}_N) ,$ (8)

en la ecuación (3). De hecho, esta es la justificación de la descomposición (5).

2 Parámetros

Las diferentes versiones de la ecuación de Schrödinger contienen los siguientes parámetros:
  • Constante de Plank, 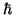$ \hbar$ : es la energía por unidad de frecuencia de cada cuanto de luz. Entra en la ecuación de Schrödinger para satisfacer las relaciones de conmutación canónicas, $ [ x_i, p_j ] = i \hbar \mathbb{I}$ .
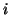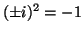  • Constante imaginaria, $ i$ : indica el carácter complejo de las funciones de onda. Representa una cantidad compleja tal que $ (\pm i)^2 = -1$ .
  • Energía propia, 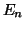$ E_n$ : valor propio del hamiloniano asociado a su n-ésimo estado propio.

3 Condiciones de validez

La ecuación de Schrödinger es útil en aquellas situaciones en que la acción del sistema (la integral temporal de la función lagrangiana) es muy pequeña, comparable al valor de la constante de Plank.

Por otra parte, la ecuación de Schrödinger deja de ser válida en las condiciones siguientes:

  • Cuando la energía cinética, 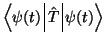$ \Braket{\psi(t)\vert\hat T\vert\psi(t)}$ es comparable a la energía en reposo, en cuyo caso son importantes las correcciones relativistas.
  • Cuando existe creación y destrucción de partículas, en cuyo caso deben utilizarse los métodos de la teoría cuántica de campos (que también pueden incorporar la relatividad).
  • La descomposición (5) y, en general, el formulismo de la ecuación independiente del tiempo tiene sentido tan solo cuando el propio hamiltoniano es también independiente del tiempo.

4 Comentarios

La ecuación de Schrödinger tan solo se puede resolver analíticamente a través del formalismo del operador de evolución, o mediante la teoría de ecuaciones diferenciales una vez se ha escrito en una base concreta (usualmente en la base de posiciones o en la de momentos).

Sin embargo, los problemas de muchas partículas (es decir, más de una), tan solo existe solución exacta para los sistemas en que la ecuación diferencial se puede separar en tantas ecuaciones mono-particulares como partículas existan.

Por otra parte, la ecuación de Schrödinger de una sola partícula (mono-particular) tiene solución analítica en los siguientes casos:

  • Problemas unidimensionales, o que por separación de variables se pueden descomponer en varias ecuaciones unidimensionales, donde el potencial es constante a trozos.
  • Problemas tridimensionales en regiones finitas, rodeadas por paredes impenetrables, con geometría adaptada a algún tipo de coordenadas curvilíneas.
  • Problemas unidimensionales con potenciales cuadráticos en la posición (oscilador harmónico, campos eléctricos y magnéticos constantes y perpendiculares entre si, etc.).

En otros casos, la solución de la ecuación de Schrödinger exige métodos numéricos, o bien simulaciones por ordenador.