Gravitación newtoniana
Barbol
Índice General
- 1. Introducción
- 2. Un poco de matemáticas
- 3. Leyes de Kepler
- 4. Ley de la gravitación universal
- 5. El problema de dos cuerpos (Matemático)
- 6. El problema de dos cuerpos (Fíico)
- 6.1 El potencial gravitatorio
- 6.2 Lagrangiana del problema de dos cuerpos
- 6.3 Teoremas de conservación - Primeras integrales
- 6.4 Ecuaciones de movimiento
- 7. Algunas consideraciones
Prólogo
En estos puntos se parte de las leyes de Kepler, que son leyes empíricas, para desarrollar la teoría gravitatoria clásica.
La primera parte corresponde a un nivel para quien ya tiene avanzado el bachillerato o está en su primer año de carrera pero aún no cursó la asignatura de mecánica.
A partir de la sección 6.2 el nivel ya requiere algunos conocimientos de mecánica analítica, aunque es asequible siempre y cuando nos creamos alguna de los resultados obtenidos.
Se han dado dos métodos diferentes para llegar a los mismos resultados, el primero es un método que he dado en llamar ``matemático'' pues se basa más en las propiedades de la elipse y en resultados matemáticos puros que en los conceptos físicos habituales. El segundo lo denominé ``físico'' y se basa en leyes de conservación generales.
En el último capítulo se dan un par de comentarios de modo muy breve y totalmente cualitativo, pero que sin embargo revierten alguna importancia: la precesión de los ápsides y el problema de la estabilidad de un tercer cuerpo.
1. Introducción
Ya desde antiguo se observó el cielo y se comprobó que existían ciertos cuerpos que no se movían igual que las estrellas, fueron llamados planetas, que significaba errantes, y fueron identificados con deidades.
En la antigua grecia se propusieron diversos sistemas para ordenar el movimiento de estos planetas. Aristarco de Samos propuso que el Sol estaba en el centro del Universo con los planetas girando a su alrededor en órbitas circulares, pero la teoría que triunfó fue la de Ptolomeo, según la cual era la Tierra la que estaba en el centro con el sol girando en torno a él. Esa teoría pasó a la cultura cristiana (y por tanto a la Edad Media europea) a través de Aristóteles y sobrevivió hasta que en la época renacentista Copérnico volvió a introducir la teoría heliocéntrica.
Por el siglo XVI un noble danés llamado Tycho Brahe y aficionado a la astronomía decidió que había que hacer anotaciones precisas de la posición de los planetas en el cielo y cúando se hacían, pues hasta entonces se trabajaban con anotaciones vagas, viejas y poco rigurosas. Pasó, pues, su vida haciendo estas anotaciones y, a su muerte, su discípulo y ayudante Kepler las heredó y trabajó con ellas hasta que encontró ciertas regularidades que expresó en forma de tres leyes en los años 1606 y 1619.
Posteriormente, a finales del s.XVII Newton publicó su ley de la gravitación universal, unificando la fuerza de atracción celeste con la fuerza de atracción terrestre. Esta ley fue considerada como válida hasta el primer cuarto del siglo XX, cuando se publicó la teoría general de la relatividad de la que la teoría de Newton es sólo una aproximación para velocidades no comparables con la velocidad de la luz.
2. Un poco de matemáticas
2.1 Coordenadas polares
Generalemente cuando queremos situar un punto en un plano euclídeo damos una tríada de números ![]() a los que denominamos coordenadas y que se refieren a ese punto de forma única y, además, a ese punto le corresponden únicamente esas coordenadas; a esta tríada se la suele denominar coordenadas cartesianas del punto.
a los que denominamos coordenadas y que se refieren a ese punto de forma única y, además, a ese punto le corresponden únicamente esas coordenadas; a esta tríada se la suele denominar coordenadas cartesianas del punto.
En ocasiones se nos presentan problemas con algún tipo de cualidad que hace aconsejable emplear otro tipo de coordenadas. Por ejemplo, en el caso del cálculo del potencial creado por una carga ![]() de acuerdo con la teoría electromagnética es muy aconsejable la utilización de coordenadas esféricas, pues este potencial tiene lo que se llama simetría esférica. En el caso de estos apuntes las coordenadas más útiles son las denominadas coordenadas polares.
de acuerdo con la teoría electromagnética es muy aconsejable la utilización de coordenadas esféricas, pues este potencial tiene lo que se llama simetría esférica. En el caso de estos apuntes las coordenadas más útiles son las denominadas coordenadas polares.
Las coordenadas polares se definen en un plano (por lo que serán dos) a partir de la distancia desde el origen de coordenadas hasta el punto en cuestión (el vector que une estos dos puntos se denomina radio-vector y el ángulo que forman ese radio-vector con el eje de abscisas de un sistema de referencia cartesiano aleatorio.
Pero es bien sabido del álgebra básica que para referirnos a un sistema de coordenadas en un plano (un espacio
![]() ) necesitaremos dos versores (vectores unitarios) que nos den una base, es decir, linealmente independientes entre si. Parece obvio escoger como uno de las componentes de la base el versor dirigido en la dirección del radio unitario y que denotamos como versor radial (
) necesitaremos dos versores (vectores unitarios) que nos den una base, es decir, linealmente independientes entre si. Parece obvio escoger como uno de las componentes de la base el versor dirigido en la dirección del radio unitario y que denotamos como versor radial (
![]() ), mientras que el otro lo escogemos girando el versor radial
), mientras que el otro lo escogemos girando el versor radial ![]() radianes en el sentido del giro, es el versor transversal (
radianes en el sentido del giro, es el versor transversal (
![]() ).
).
Se puede ver en la imagen (2.1) que las expresiones para estos dos versores son:
A diferencia de los versores base del espacio cartesiano
![]() en el que éstos permanecían siempre constantes, los versores polares varían con la posición del punto, de modo que si éste punto depende de un parámetro
en el que éstos permanecían siempre constantes, los versores polares varían con la posición del punto, de modo que si éste punto depende de un parámetro ![]() entonces el versor radial (y por definición el versor transversal) también variarán. Calculemos cómo son estas variaciones:
entonces el versor radial (y por definición el versor transversal) también variarán. Calculemos cómo son estas variaciones:
en donde
Por tanto vemos que la derivada de un versor polar es linealmente dependientes del otro versor, lo cual es una suerte pues hace innecesario el cálculo de la derivada segunda de los versores, que aparecerá en el desarrollo de la teoría gravitatoria.
2.2 Velocidad y aceleración en polares
Tenemos que, por definición, el vector posición de un punto en polares tiene la forma
![]() donde
donde ![]() es el módulo o distancia y
es el módulo o distancia y
![]() el versor radial. Veamos ahora cómo es el vector velocidad:
el versor radial. Veamos ahora cómo es el vector velocidad:
El primer término de la suma se corresponde con la velocidad radial y el segundo con la velocidad transversal (existe si varía el ángulo
En el caso de la aceleración tenemos:
El primer término se corresponde con la aceleración radial y en él se puede diferenciar el término correspondiente a la aceleración del cuerpo y a la aceleración centrífuga (que se opone a él); el segundo término se corresponde a la aceleración tangencial y se diferencia entre la aceleración de coriolis y la aceleración angular.
2.3 Cónicas
Las curvas cónicas son conocidas y estudiadas desde la antiguedad y reciben el nombre general de cónicas por ser las curvas correspondientes a los cortes de un plano con un cono. Estas curvas reciben nombres diferentes dependiendo de sus características: círculo, elipse, parábola e hipérbola y presentan algunas regularidades que hace que sea útil la introducción de un punto denominado foco.
En general las ecuaciones en cartesianas correspondientes a estas curvas cuando están situadas en un sistema de coordenadas propio son las siguientes:
| Curva | Ecuación | Constantes (referidas al foco) |
| Círculo |
|
|
| Elipse |
|
|
| Parábola | ||
| Hipérbola |
|
|
|
|
En el caso de la elipse (que nos va a interesar especialmente) los focos están a una distancia del origen igual a
![]() sobre el semieje mayor; generalmente a esta distancia se le llama
sobre el semieje mayor; generalmente a esta distancia se le llama
![]() en donde
en donde ![]() es la excentricidad de la elipse.
es la excentricidad de la elipse.
2.3.1 Las cónicas en polares
Vimos en la tabla de la sección anterior las diferentes ecuaciones en coordenadas cartesianas para las curvas cónicas, sin embargo estas expresiones difieren bastante unas de otras y es complicado estudiar su comportamiento en general. Sin embago, cuando pasamos de la forma cartesiana de estas ecuaciones a la forma polar (situando el polo en uno de los focos) encontramos que todas ellas se pueden escribir de la forma
donde
| Curva | Parámetro | Excentricidad |
| Círculo | ||
| Elipse |
|
|
| Parábola | ||
| Hipérbola |
|
3. Leyes de Kepler
3.1 Enunciado de las leyes de Kepler
De los datos recopilados por Tycho Brahe Kepler dedujo tres leyes acerca del movimiento de los planetas. Las dos primeras datan del año 1609 y fueron publicadas en su libro Astronomia Nova, la tercera es del año 1619 y fue publicada en la obra Harmonices Mundi Libri V. Generalmente se enuncian como sigue:
Primera ley
Los planetas describen órbitas elípticas en torno al Sol con éste en uno de sus focos.
Segunda ley
El radio-vector que une el Sol con un planeta barre áreas iguales en tiempos iguales.
Tercera ley
La razón del cubo semieje mayor de una órbita respecto al período al cuadrado del planeta permanece constante.
Más adelante comprobaremos que la primera ley de Kepler se puede generalizar a cualquier tipo de cónica y que la tercera ley de Kepler no es exactamente cierta (sólo es válida cuando la masa de uno de los cuerpos involucrados es despreciable frente a la masa del otro cuerpo).
3.2 Forma matemática de las leyes de Kepler
Conviene expresar matemáticamente las tres leyes de Kepler para poder trabajar con ellas. Veremos que las expresiones de las leyes primera y tercera son triviales, mientras que la expresión matemática de la segunda ley se deduce fácilmente.
3.2.1 Primera ley
Los planetas describen órbitas elípticas en torno al Sol con éste en uno de sus focos.
Es decir, situando el Sol en un foco y llamando ![]() a la distancia entre el Sol y el planeta tenemos que
a la distancia entre el Sol y el planeta tenemos que
en donde
3.2.2 Segunda ley
El radio-vector que une el Sol con un planeta barre áreas iguales en tiempos iguales.
A partir de la imagen (3.2.2) se observa que
![]() , donde
, donde
![]() es el vector superficie del triángulo sombreado en la figura. El cambio de este vector con el tiempo será pues:
es el vector superficie del triángulo sombreado en la figura. El cambio de este vector con el tiempo será pues:
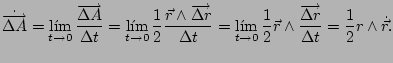
Según la segunda ley de Kepler esta velocidad areolar es constante, con lo que tenemos que en polares el módulo es:
3.2.3 Tercera ley
La razón del cubo semieje mayor de una órbita respecto al período al cuadrado del planeta permanece constante.
Matemáticamente eso se expresa del modo:
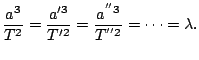
4. Ley de la gravitación universal
Newton publicó en sus Principia Mathematica de 1687 la ley de la gravitación universal que explicaba tanto el movimiento orbital de los objetos celestes como la atracción gravitatoria de los cuerpos sobre la Tierra. Esta ley se puede deducir a partir de la segunda ley de newton de la mecánica clásica y las leyes de kepler y fue considerada como perfectamente válida durante más de doscientos años, hasta que Einstein publicó en 1915 su teoría general de la relatividad, de la que la teoría de Newton era un caso especial a pequeñas velocidades.
La forma matemática de la fuerza que el cuerpo ![]() ejerce sobre un cuerpo
ejerce sobre un cuerpo ![]() es
es
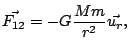
en donde
Hay que hacer notar que bajo la forma anterior de la ley sólo se podría aplicar a masas puntuales, es decir, partículas que tienen toda la masa concentrada en ellas y, si quisiéramos tratar a un cuerpo que ocupe un volumen determinado debemos hacer la suposición de que se puede tratar como una partícula puntual con la masa del cuerpo antes de trabajar con él. Esto implica que la fuerza gravitatoria es lineal (la fuerza total es la suma de todas las fuerzas que actúan). En realidad se comenta que esto es así más adelante, en la sección 6.1.1, con lo que durante hasta esa sección el hecho se dará por cierto sin demostración.
4.1 Deducción de la ecuación de la gravitación universal
De la segunda ley de Newton de la mecánica clásica tenemos que
![]() lo que, sustituyendo la expresión para la aceleración obtenida en la sección 2.2 y aplicada al caso en el que un cuerpo
lo que, sustituyendo la expresión para la aceleración obtenida en la sección 2.2 y aplicada al caso en el que un cuerpo ![]() atrae a un cuerpo
atrae a un cuerpo ![]() tenemos que en general:
tenemos que en general:
Si ahora tomamos la segunda ley de Kepler (sección 3.2.2) y derivamos con respecto al tiempo tenemos:
donde dividimos por
Para ver cuánto vale la resta
![]() debemos obtener el valor de
debemos obtener el valor de ![]() (tomamos la primera ley de Kepler (sección 3.2.1) y derivamos dos veces respecto al tiempo) y el valor de
(tomamos la primera ley de Kepler (sección 3.2.1) y derivamos dos veces respecto al tiempo) y el valor de
![]() como se comprueba fácilmente a partir de la segunda ley de Kepler. Para
como se comprueba fácilmente a partir de la segunda ley de Kepler. Para ![]() tenemos pues:
tenemos pues:
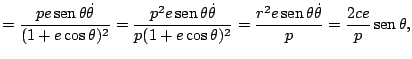 |
||
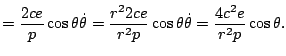 |
Por tanto el valor de la aceleración radial es:
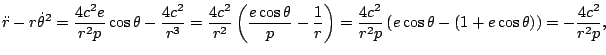
con lo que la expresión de la fuerza de la gravedad queda como:
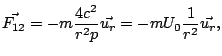
donde se agruparon en el término
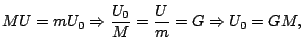
y finalmente llegamos a:
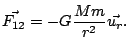
5. El problema de dos cuerpos (Matemático)
Hemos visto que las leyes de Kepler implican la ley de la gravitación universal de Newton, pero para comprobar que ambas son equivalentes tenemos que ver si la ley de Newton implica necesariamente las leyes de Kepler, este problema se conoce como el problema de los dos cuerpos.
5.1 El centro de masas
Supongamos que tenemos dos masas puntuales y, como tales, se atrae según la ley de gravitación de Newton. Para conocer la posición de los cuerpos tendremos que integrar dos veces la ecuación vectorial de Newton, lo que implica que será necesario dar seis cantidades diferentes para tener el problema totalmente resuelto. Estas cantidades pueden ser las tres componentes de los vectores posición de cada una de las partículas o bien tomar las tres componentes del vector posición del centro de masas
![]() y las tres componentes del vector
y las tres componentes del vector
![]() que nos da la posición relativa del segundo cuerpo respecto al primero.
que nos da la posición relativa del segundo cuerpo respecto al primero.
Escogiendo esta segunda posibilidad la solución corresponde a observar cómo evoluciona espacialmente el centro de masas y cómo se mueve un cuerpo respecto al otro. Partiendo de
![]() ,
,
![]() y
y
![]() tenemos que
tenemos que
![]() , que al integrarlo dos veces nos queda
, que al integrarlo dos veces nos queda
![]() . Finalmente, dividiendo por
. Finalmente, dividiendo por
![]() obtenemos que
obtenemos que
![]() , es decir, el centro de masas se mueve con un movimiento rectilíneo uniforme y podemos escoger un sistema de referencia en el que esté en reposo.
, es decir, el centro de masas se mueve con un movimiento rectilíneo uniforme y podemos escoger un sistema de referencia en el que esté en reposo.
5.2 Movimiento relativo de los dos cuerpos
Tenemos que
![]() ,
,
![]() . Si simplificamos las expresiones y las restamos obtenemos la ecuación
. Si simplificamos las expresiones y las restamos obtenemos la ecuación
![]() donde agrupamos en el término
donde agrupamos en el término ![]() las constantes y expresamos el versor como el cociente entre el vector y su módulo. Resolviendo esta ecuación diferencial vectorial de segundo orden que nos da el movimiento relativo entre los cuerpos tendremos ya totalmente resuelto el problema. Este movimiento recibe el nombre de movimiento kepleriano.
las constantes y expresamos el versor como el cociente entre el vector y su módulo. Resolviendo esta ecuación diferencial vectorial de segundo orden que nos da el movimiento relativo entre los cuerpos tendremos ya totalmente resuelto el problema. Este movimiento recibe el nombre de movimiento kepleriano.
5.2.1 Primeras integrales
Si tomamos la ecuación diferencial vectorial anterior y calculamos el producto
![]() observamos que es igual a cero, con lo cual su integral primera será igual a una constante. Si diferenciamos
observamos que es igual a cero, con lo cual su integral primera será igual a una constante. Si diferenciamos
![]() respecto al tiempo vemos que nos da justamente el producto vectorial anterior, por lo que
respecto al tiempo vemos que nos da justamente el producto vectorial anterior, por lo que
![]() donde
donde ![]() es un vector constante. Además vemos que este producto vectorial es justamente el doble de la velocidad areolar, con lo cual hemos llegado a la segunda ley de Kepler.
es un vector constante. Además vemos que este producto vectorial es justamente el doble de la velocidad areolar, con lo cual hemos llegado a la segunda ley de Kepler.
Si ahora hacemos el producto mixto
![]() , con lo que el vector posición de un cuerpo respecto a otro es permanentemente perpendicular a un vector constante, esto implica que el movimiento se da en un plano.
, con lo que el vector posición de un cuerpo respecto a otro es permanentemente perpendicular a un vector constante, esto implica que el movimiento se da en un plano.
5.2.2 Segundas integrales
Más adelante necesitaremos las siguientes dos relaciones:
![]() y
y
![]() . Esta segunda se demuestra derivando respecto al tiempo la igualdad
. Esta segunda se demuestra derivando respecto al tiempo la igualdad
![]() .
.
![$\displaystyle =-\gamma\frac{\vec{r}}{r^{3}}\wedge(\vec{r}\wedge\dot{\vec{r}})=-...
...{r}}\right]=-\frac{nu}{r^{3}}\left[(r\dot{r})\vec{r}-r^{2}\dot{\vec{r}}\right],$](img99.png) |
||
![$\displaystyle =-\frac{\gamma}{r^{2}}[\dot{r}\vec{r}-r\dot{\vec{r}}]=\gamma\frac...
...\rm d\!}\nolimits }{\mathop{\rm d\!}\nolimits t}\left(\frac{\vec{r}}{r}\right).$](img100.png) |
Lo que, al integrar, se convierte en
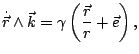
donde
Si ahora multiplicamos escalarmente ![]() por
por
![]() obtenemos:
obtenemos:
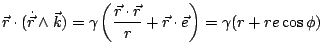 |
en donde pusimos
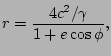
que es la ecuación polar de las cónicas con parámetro igual a
Hay que hacer notar que aún no tenemos resuelto totalmetne el problema, los vectores que hemos empleado para las integraciones (![]() y
y ![]() son perpendiculares entre si y por lo tanto sólo cinco de sus seis componentes son independientes entre si, aún nos falta relacionar el vector posición con el tiempo, esto lo haremos al formular la ecuación de Kepler, en la sección 5.3.
son perpendiculares entre si y por lo tanto sólo cinco de sus seis componentes son independientes entre si, aún nos falta relacionar el vector posición con el tiempo, esto lo haremos al formular la ecuación de Kepler, en la sección 5.3.
5.2.3 Deducción de la tercera ley de Kepler
Ya vimos en la sección 3.2.3 que según Kepler la razón entre el cubo del semieje mayor y el cuadrado del período es constante. Veremos que esto no es del todo cierto.
Durante el desarrollo de las ecuaciones obtuvimos las igualdades
![]() en donde la última igualdad es válida para las órbitas elípticas (ya que usamos el parámetro de la elipse), como es el caso de las órbitas de los planetas.
en donde la última igualdad es válida para las órbitas elípticas (ya que usamos el parámetro de la elipse), como es el caso de las órbitas de los planetas.
Para saber el valor de ![]() (recordemos, la velocidad areolar) nos fijamos en que el área recorrida en el período de la órbita es toda la elipse, de este modo tenemos que
(recordemos, la velocidad areolar) nos fijamos en que el área recorrida en el período de la órbita es toda la elipse, de este modo tenemos que
![]() , donde se usa el resultado
, donde se usa el resultado
![]() . Por tanto tenemos:
. Por tanto tenemos:
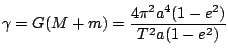 |
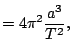 |
|
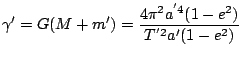 |
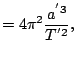 |
con lo cual obtenemos el resultado
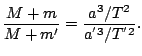
Esa expresión sólo es una constante cuando ![]() y se aproxima mucho cuando
y se aproxima mucho cuando ![]() , como es el caso del Sol y los planetas (salvo los gigantes gaseosos, como Júpiter).
, como es el caso del Sol y los planetas (salvo los gigantes gaseosos, como Júpiter).
Con este resultado observamos que a partir de la ecuación de gravitación universal de Newton podemos llegar a obtener las tres leyes empíricas de Kepler, por lo que ambas son equivalentes y por tanto hablar de las leyes de Kepler implica, necesariamente, hablar de la ley de Newton.
5.2.4 Integral de la energía. Velocidad del cuerpo orbitante
Pasaremos ahora a resolver la integral de la energía, ésta no es una energía desde el punto de vista físico, es un resultado matemático que nos ayuda a conocer cuánto valdrá el módulo del vector velocidad del cuerpo orbitante en cada punto de su órbita. Para una discusión más rigurosa acerca de la energía véase más adelante la sección 6.3.4. El desarrollo es el que sigue:
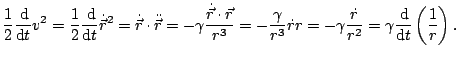
Si ahora integramos esa igualdad llamando a la constante de integración integral de la energía y la denotamos por ![]() obtenemos el resultado
obtenemos el resultado
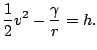
Ahora tendremos en cuenta resultados anteriores para llegar al valor del módulo de la velocidad:
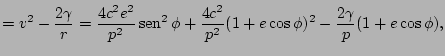 |
||
De este modo llegamos a:
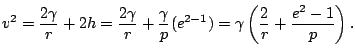
Por tanto vemos que la velocidad depende de la distancia de la partícula al foco, la constante ![]() que depende de la masa y el parámetro y la excentricidad de la órbita. La siguiente tabla es un resumen de los cuatro casos posibles para estos valores.
que depende de la masa y el parámetro y la excentricidad de la órbita. La siguiente tabla es un resumen de los cuatro casos posibles para estos valores.
| Circular | Elíptico | Parabólico | Hiperbólico | |
| Excentricidad | ||||
| Parámetro |
|
|
||
| Integral energía |
|
|
0 | |
| Velocidad cuadrado |
|
|
Como podemos observar el valor de la integral de la energía es negativo cuando la órbita es cerrada. Este resultado es más importante de lo que parece a simple vista, ya que nos permite saber qué tipo de órbita tenemos sólo con conocer el valor de la energía; esto se estudiará con más detalle en la sección 6.3.4.
5.3 Ecuación de Kepler
Esta ecuación también se conoce como ley horaria del movimiento kepleriano elíptico y es la que nos relaciona la posición de un cuerpo con el tiempo. Para empezar definimos el movimiento medio como ![]() , resultado que implica que
, resultado que implica que
![]() .
.
Ahora bien, en la sección anterior obtuvimos el resultado
![]() y sabemos que
y sabemos que
![]() , por tanto:
, por tanto:
![$\displaystyle \dot{r}^{2}=n^{2}a^{3}\left(\frac{2}{r}-\frac{1}{a}\right)-\frac{n^{2}a^{4}(1-e^{2})}{r^{2}}=\frac{n^{2}a^{2}}{r^{2}}[a^{2}e^{2}-(a-r)^{2}],
$](img144.png)
por tanto, sacando la raíz cuadrada, obtenemos la ecuación que liga la distancia
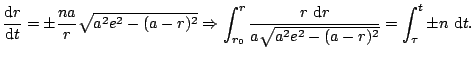
Esta integral no es fácil de resolver en principio, pero realizando el cambio de variable
![]() y escogemos el signo positivo nos queda:
y escogemos el signo positivo nos queda:
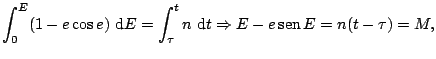
ecuación conocida como ecuación de Kepler y que no tiene solución analítica, con lo que está tabulada y se tiene que resolver mediante aproximaciones. Durante la resolución de la ecuación diferencial nos vimos obligados a introducir dos nuevas variables: mientras
6. El problema de dos cuerpos (Físico)
Ya hemos resuelto completamente el problema de dos cuerpos de un modo bastante alejado de conceptos físicos habituales como son la energía o las leyes de simetría. En esta sección nos ocuparemos de este caso a partir de la mecánica analítica y terminaremos concluyendo de nuevo las ecuaciones de Kepler como consecuencias físicas.
6.1 El potencial gravitatorio
A partir de la ley de gravitación universal vemos que la fuerza gravitatoria entre el Sol y los planetas uno a uno es
![]() en donde
en donde ![]() es la masa del Sol y
es la masa del Sol y ![]() la masa del planeta correspondiente. Es decir, en el cálculo de la fuerza gravitatoria que ejerce el Sol sobre otro cuerpo siempre aparece el término
la masa del planeta correspondiente. Es decir, en el cálculo de la fuerza gravitatoria que ejerce el Sol sobre otro cuerpo siempre aparece el término
![]() al que denominaremos campo gravitatorio producido por el Sol. Podemos generalizar la expresión al campo producido por cualquier cuerpo sin más que sustituír la masa del Sol por la masa del cuerpo tratado.
al que denominaremos campo gravitatorio producido por el Sol. Podemos generalizar la expresión al campo producido por cualquier cuerpo sin más que sustituír la masa del Sol por la masa del cuerpo tratado.
Este campo vectorial tiene dimensiones de fuerza partido por masa, es decir, dimensiones de aceleración. Si calculamos el campo creado por la Tierra en la superficie de ésta (es decir, ![]() es la masa terrestre y
es la masa terrestre y ![]() el radio terrestre) obtenemos un valor aproximado de
el radio terrestre) obtenemos un valor aproximado de
![]() , valor de sobra conocido. Ahora podemos manejar un poco la expresión del campo gravitatorio para llegar a un resultando muy interesante:
, valor de sobra conocido. Ahora podemos manejar un poco la expresión del campo gravitatorio para llegar a un resultando muy interesante:
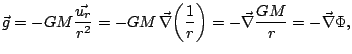
es decir, el campo gravitatorio se puede escribir como gradiente de un campo escalar, lo cual implica que el campo gravitatorio es conservativo. Esta función
Hay que hacer notar que para definir ![]() tenemos que realizar una integral y por tanto el potencial gravitatorio no está completamente determinado, sólo las diferencias de potencial son significativas. Generalmente esto se soluciona atribuyendo el valor
tenemos que realizar una integral y por tanto el potencial gravitatorio no está completamente determinado, sólo las diferencias de potencial son significativas. Generalmente esto se soluciona atribuyendo el valor ![]() a
a ![]() . Con esta convención la expresión para el potencial es:
. Con esta convención la expresión para el potencial es:
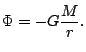
Si la masa no es la de una partícula potencial, sinó que se trata de una distribución volumétrica de densidad ![]() , o bien una superficial de densidad
, o bien una superficial de densidad ![]() o bien una lineal de densidad
o bien una lineal de densidad ![]() tenemos respectivamente que:
tenemos respectivamente que:
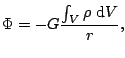 |
|
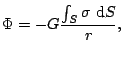 |
|
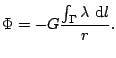 |
Si calculamos el trabajo por unidad de masa que debe realizarse sobre un cuerpo situado en un campo gravitatorio para desplazarlo una distancia
![]() tenemos:
tenemos:
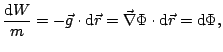
es decir, la diferencia de potencial gravitatorio nos da el trabajo por unidad de masa necesario para trasladar un cuerpo de un punto a otro dentro de un campo gravitatorio. Entonces, para calcular el trabajo necesario tendremos que multiplicar la variación de potencial gravitatorio por la masa del cuerpo en cuestión, esta nueva función se denomina energía potencial y es igual a
En definitiva, un cuerpo cualquiera, por el simple hecho de estar en un campo gravitatorio, tendrá asociado una energía potencial que se suele referir como energía potencial ``del cuerpo'', a pesar de estar asociada a la presencia del campo.
6.1.1 Campo exterior de una esfera maciza y una hueca
Para calcular el campo exterior de una esfera hueca de radio interior ![]() , radio exterior
, radio exterior ![]() y densidad homogénea
y densidad homogénea ![]() tenemos que calcular la integral
tenemos que calcular la integral
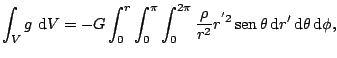
en donde
6.2 Lagrangiana del problema de dos cuerpos
Ya se ha visto anteriormente que el centro de masas en el problema de dos cuerpos se mueve a velocidad uniforme. Por otro lado se puede demostrar que los vectores que van desde el centro de masas a cada uno de los cuerpos ![]() y
y ![]() son
son
![]() y
y
![]() .
.
Por otra parte la lagrangiana de un sistema de dos partículas será la suma de las energías cinéticas de las dos partículas menos la energía potencial, es decir,
![]() . Juntando esta expresión con las dos anteriores tenemos que la lagrangiana queda en la forma
. Juntando esta expresión con las dos anteriores tenemos que la lagrangiana queda en la forma
![]() , donde
, donde
![]() es la masa reducida del sistema, es decir, la lagrangiana es equivalente a la de una sola partícula con masa la masa reducida del sistema en un campo con potencial
es la masa reducida del sistema, es decir, la lagrangiana es equivalente a la de una sola partícula con masa la masa reducida del sistema en un campo con potencial ![]() . Una vez resuelto el problema se pueden volver a calcular los vectores
. Una vez resuelto el problema se pueden volver a calcular los vectores
![]() y
y
![]() , pero esto carece de interés en la mayoría de los casos y es más útil conocer el movimiento relativo de los cuerpos.
, pero esto carece de interés en la mayoría de los casos y es más útil conocer el movimiento relativo de los cuerpos.
6.3 Teoremas de conservación - Primeras integrales
Al haber eliminado del estudio el movimiento del centro de masas por ser éste uniforme la conservación del momento lineal no añade nada nuevo a la descripción del movimiento, así que no se discutirá.
6.3.1 Conservación del momento angular
Como la energía potencial de la partícula sólo depende de la distancia de ésta al centro de masas el problema posee un tipo de simetría que se denomina simetría esférica, es decir, el comportamiento de la partícula no depende de la orientación de ésta, sinó sólo (como ya se ha apuntado) de su distancia al centro de masas. Bajo estas condiciones decimos que el momento angular del sistema se conserva, es decir,
![]() .
.
Esta relación implica que el vector posición y el vector momento son siempre perpendiculares a un vector constante, por lo que tenemos que el movimiento ocurre en un plano. Si ahora expresamos nuestra lagrangiana en coordenadas polares tenemos
![]() y resolviendo la ecuación de lagrange para el ángulo obtenemos:
y resolviendo la ecuación de lagrange para el ángulo obtenemos:
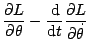 |
||
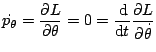 |
||
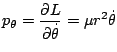 |
Por tanto la cantidad
![]() constituye una integral primera del movimiento que denotaremos
constituye una integral primera del movimiento que denotaremos ![]() y va asociada al momento angular, permaneciendo constante con el tiempo. El significado geométrico de este valor es evidente, recordando que la velocidad areolar es
y va asociada al momento angular, permaneciendo constante con el tiempo. El significado geométrico de este valor es evidente, recordando que la velocidad areolar es
![]() tenemos la segunda ecuación de Kepler como consecuencia de la conservación del momento angular.
tenemos la segunda ecuación de Kepler como consecuencia de la conservación del momento angular.
6.3.2 Conservación de la energía
Ante la ausencia de fuerzas disipativas tenemos que la energía total ![]() de un sistema se conserva, en el problema que estamos tratando la expresión toma la forma siguiente:
de un sistema se conserva, en el problema que estamos tratando la expresión toma la forma siguiente:
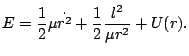
6.3.3 Energía centrífuga. Potencial efectivo
En la expresión de la energía podemos diferenciar tres sumandos que pasamos a asociar a los tipos de energía habituales. El primer sumando se reconoce fácilmente como la energía cinética de la partícula de masa ![]() , ya que
, ya que ![]() es la velocidad a la que se traslada. El tercer sumando es la forma genérica del otencial con el que estamos tratando.
es la velocidad a la que se traslada. El tercer sumando es la forma genérica del otencial con el que estamos tratando.
Es el segundo sumando el que hay que analizar más en detalle, tenemos que la energía la podemos expresar mediante
![]() , si la consideramos como una energía potencial podemos calcular su fuerza asociada como
, si la consideramos como una energía potencial podemos calcular su fuerza asociada como
![]() , que no es ni más ni menos que la fuerza centrífuga, una fuerza fictícea que aparece en sistemas giratorios. Por tanto, podemos considerar que la energía del problema en cuestión se puede separar en la energía cinética de la partícula y un potencial efectivo que agrupa tanto al potencial gravitatorio como al potencial centrífugo:
, que no es ni más ni menos que la fuerza centrífuga, una fuerza fictícea que aparece en sistemas giratorios. Por tanto, podemos considerar que la energía del problema en cuestión se puede separar en la energía cinética de la partícula y un potencial efectivo que agrupa tanto al potencial gravitatorio como al potencial centrífugo:
![]() .
.
En el caso del potencial gravitatorio vemos que el potencial toma la forma
![]() , con lo cual el potencial efectivo es
, con lo cual el potencial efectivo es
![]() , que se anula en el infinito debido a la elección de que
, que se anula en el infinito debido a la elección de que
![]() .
.
6.3.4 Estudio cualitativo de las órbitas
Teniendo en cuenta las consideraciones anteriores acerca de la energía podemos sacar algunas conclusiones. En la imagen (6.3.3) podemos diferenciar tres regiones. En la primera tenemos ![]() y el movimiento no está confinado. Una partícula con esos niveles de energía vendrá desde el infinito hasta encontrarse con una barrera de potencial en su
y el movimiento no está confinado. Una partícula con esos niveles de energía vendrá desde el infinito hasta encontrarse con una barrera de potencial en su ![]() que provocará su progresivo alejamiento creciendo
que provocará su progresivo alejamiento creciendo ![]() indefinidamente. Hay que tener en cuenta que la velocidad de la partícula en un punto
indefinidamente. Hay que tener en cuenta que la velocidad de la partícula en un punto ![]() determinado será la diferencia entre la energía
determinado será la diferencia entre la energía ![]() que posea la partícula y el valor de
que posea la partícula y el valor de ![]() .
.
Cuando la energía total sea negativa (estos valores negativos se deben a la exigencia de que el potencial se anule en el infinito, nada más) y su valor se encuentra entre cero y el valor mínimo del potencial efectivo la partícula oscilará entre un ![]() y un
y un ![]() , que son las distancias apsidales de la órbita.
, que son las distancias apsidales de la órbita.
Si la energía coincide con el valor mínimo del potencial efectivo entonces la partícula siempre se encuentra a una distancia ![]() fija, siendo
fija, siendo ![]() y el movimiento será, por tanto, circular.
y el movimiento será, por tanto, circular.
Para valores inferiores al valor mínimo del potencial efectivo no existen movimientos reales, pues implicarían velocidades imaginarias.
6.4 Ecuaciones de movimiento
A partir de la expresión de conversación de la energía podemos despejar ![]() y obtenemos:
y obtenemos:
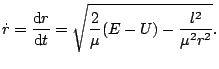
De este modo podemos obtener ![]() y, por lo tanto,
y, por lo tanto, ![]() y el problema estaría solucionado, sin embargo resulta de mayor interés obtener la trayectoria en función de
y el problema estaría solucionado, sin embargo resulta de mayor interés obtener la trayectoria en función de ![]() y
y ![]() . Haciendo
. Haciendo
![]() y sustituyendo los valores ya conocidos de
y sustituyendo los valores ya conocidos de
![]() y
y ![]() (que es la ecuación anterior) obtenemos:
(que es la ecuación anterior) obtenemos:
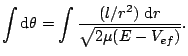
Si sustituímos el valor del potencial efectivo en la ecuación y hacemos el cambio de variables ![]() obtenemos:
obtenemos:
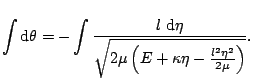
Resolviendo esta integral por medio de tablas obtenemos que
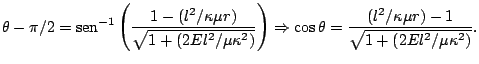
Que, como se puede ver sin más que un simple juego algebraico, es la ecuación en coordenadas polares para una cónica con uno de los focos centrado en el polo en la que el parámetro vale
![]() y la excentricidad está relacionada con la energía mediante
y la excentricidad está relacionada con la energía mediante
![]() , esto se corresponde con la primera ecuación de Kepler y es, como vimos, una consecuencia de la conservación de la energía.
, esto se corresponde con la primera ecuación de Kepler y es, como vimos, una consecuencia de la conservación de la energía.
Con esa correspondencia entre la excentricidad y la energía podemos volver hacer la siguiente relación:
| Energía | Excentricidad | Órbita |
| No tiene sentido | ||
| Circular | ||
|
|
Elíptica | |
| Parabólica | ||
| Hiperbólica |
Ahora se pueden repetir casi igualmente los pasos de las secciones 5.2.3, 5.2.4 y 5.3 para llegar a encontrar la tercera ley de Kepler y la ecuación de Kepler, por lo cual no lo repetiremos aquí.
7. Algunas consideraciones
7.1 Precesión de los ápsides
El hecho de que la fuerza de la gravedad varíe con la inversa del cuadrado de la distancia de los cuerpos implica que toda órbita elípticaes perfectamente cerrada, es decir, el punto en el que se encuentran los ápsides no variará. Fue Newton quien apuntó esta cualidad y la propuso como método para falsar su teoría.
Estrictamente es de esperar una pequeña precesión de los ápsides, una variación de su posición cuando el cuerpo realiza una órbita completa debido a la influencia de los otros cuerpos del Sistema Solar. Esta precesión es muy pequeña y se detecta mejor en los planetas interiores. Por ejemplo, para Mercurio se comprobó que la precesión equivale a 574 segundos de arco por siglo. Cálculos detallados probaron que la precesión que cabría esperar como influencia de los otros planetas es de 531 segundos de arco por siglo, había por tanto un déficit de 43 segundos de arco por siglo sin explicación.
Se hicieron cálculos para intentar determinar un posible planeta interior más cercano al Sol que Mercurio, al que incluso se le llegó a llamar Vulcano, sin embargo este planeta nunca se encontró donde debería estar para explicar las imprecisiones de Mercurio. Fue con la llegada de la teoría general de la relatividad que se consiguió explicar este déficit de 43 segundos de arco merced a un término que, si se desprecia por ser pequeño, nos conduce a la expresión de Newton de la ley universal de la gravitación.
7.2 El problema de tres cuerpos
Hemos visto que el problema de dos cuerpos es completamente resoluble, sin embargo si añadimos un tercer cuerpo al sistema nos encontramos ante unas complicaciones que hacen que, en general, el problema no sea resoluble de forma analítica y hay que abordarlos con herramientas como la teoría de perturbaciones.
Otro problema de interés es el problema restringido de tres cuerpos, es decir, suponiendo que la masa del tercer cuerpo es despreciable frente a la de los otros dos tendríamos que encontrar los lugares donde ese cuerpo se podría encontrar en equilibrio estable (ya que la presencia de este cuerpo no perturba a la órbita relativa de los otros dos).
Este problema fue resuelto por Lagrange, que encontró cinco puntos de equilibrio en los que un tercer cuerpo se movería a la par con el otro sistema. Por ejemplo, en el sistema Sol-Tierra el tercer cuerpo orbitaría a la misma velocidad que la Tierra. De estos cinco puntos tres (![]() ,
, ![]() y
y ![]() ) corresponden a un equilibrio inestable y los otros dos (
) corresponden a un equilibrio inestable y los otros dos (![]() y
y ![]() ) a equilibrio estable.
) a equilibrio estable.
El punto ![]() permite una visión constante del Sol y por eso en él está situado el observatorio solar SOHO, en el punto
permite una visión constante del Sol y por eso en él está situado el observatorio solar SOHO, en el punto ![]() , que siempre estará tapado del Sol por la Tierra, se prevee situar un telescopio espacial. Estos dos satélites se tienen que estabilizar aproximadamente cada tres semanas.
, que siempre estará tapado del Sol por la Tierra, se prevee situar un telescopio espacial. Estos dos satélites se tienen que estabilizar aproximadamente cada tres semanas.
En los puntos estables ![]() y
y ![]() se prevee encontrar asteroides y partículas de polvo que cayeron en ese pozo de potencial. En efecto, se han encontrado estos asteroides (que se suelen llamar griegos y troyanos o simplemente troyanos) en dichos puntos en diversos sistemas, por ejemplo, los sistemas Sol-Tierra, Tierra-Luna, Sol-Júpiter, Sol-Saturno..., con lo cual la solución al problema obtiene un importante respaldo como solución útil y no una simple curiosidad académica, como fue considerado durante mucho tiempo.
se prevee encontrar asteroides y partículas de polvo que cayeron en ese pozo de potencial. En efecto, se han encontrado estos asteroides (que se suelen llamar griegos y troyanos o simplemente troyanos) en dichos puntos en diversos sistemas, por ejemplo, los sistemas Sol-Tierra, Tierra-Luna, Sol-Júpiter, Sol-Saturno..., con lo cual la solución al problema obtiene un importante respaldo como solución útil y no una simple curiosidad académica, como fue considerado durante mucho tiempo.


![\includegraphics[width=0.3\textwidth]{polar}](img3.png)
![\includegraphics[width=0.25\textwidth]{areolar}](img46.png)
![\includegraphics[width=0.4\textwidth]{cm}](img76.png)
![\includegraphics[width=0.4\textwidth]{kepler}](img139.png)
![\includegraphics[width=0.4\textwidth]{centro}](img172.png)
![\includegraphics[width=0.4\textwidth]{efec}](img201.png)
![\includegraphics[width=0.4\textwidth]{trojans}](img226.png)