Teorema de no clonado

pod

Date: Noviembre 2004

1 El teorema

1.1 Enunciado

El teorema de no clonado asegura que no existe ningún procedimiento por el cual pueda copiarse un el estado cuántico de un sistema a otro sistema idéntico.

Consideramos que el estado del sistema a copiar viene dado por un ket de estado $\Ket{\alpha}$ . Disponemos un sistema físico idéntico al primero en el cual tenemos la intención de copiar el estado del primer sistema. El inicial estado de este segundo subsistema, $\Ket\beta$ , no nos interesa, lo único que nos interesa es que el estado final del sistema en su conjunto sea de la forma $\Ket\alpha \otimes \Ket\beta$ .

Consideremos una base de estado $\Ket{a_i}$ , según la cual podemos descomponer el estado a copiar,

$\displaystyle \Ket\alpha = \sum_i a_i \Ket{a_i} .$

(1)

El procedimiento de copiado vendrá representado mediante un operador unitario y lineal. Si el procedimiento de clonado ha de funcionar, el operador debe ser capaz de duplicar los vectores de la base,

$\displaystyle U \Ket{a_i} \otimes \Ket\beta = \Ket{a_i} \otimes \Ket{a_i} .$

(2)

Veamos, pues, el resultado de aplicar el operador de clonado al estado completo,

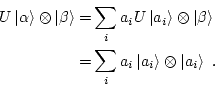$\begin{equation*}\begin{aligned}U \Ket\alpha \otimes \Ket\beta = & \sum_i a_i U ... ...a \ = & \sum_i a_i \Ket{a_i} \otimes \Ket{a_i} . \end{aligned}\end{equation*}$

Sin embargo, este estado no es $\Ket\alpha \otimes \Ket\alpha$ , que se descompone de la forma

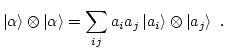$\displaystyle \Ket\alpha \otimes \Ket\alpha = \sum_{ij} a_i a_j \ket{a_i} \otimes \ket{a_j} .$

(4)

Por lo tanto, el procedimiento de clonado funcionará tan sólo si

$\displaystyle a_i a_j = a_i \delta_{ij} ,$

(5)

lo cual, en general, no es cierto.

1.3 Comentarios

El teorema de no clonado fue formulado por primera vez por Wootters, Zurek y Dieks en 1982. La simplicidad de su demostración sorprendió a la comunidad científica, que no entendía como pudo pasar inadvertido a tantas generaciones de físicos, sobre todo por sus importantísimas implicaciones y los grandes esfuerzos de investigación en esta temática que, a lo largo de la segunda mitad del siglo XX, se llevó a cabo por una gran cantidad de científicos.

2 Implicaciones

2.1 En la computación cuántica

El teorema de no clonado impone fuertes restricciones a los adelantos en computación cuántica, ya que impide realizar copias de seguridad de los datos, almacenarlos de forma permanente etc. El mismo procedimiento de computación cuántica queda dificultado, ya que no es posible registrar los estados intermedios para la detección --y corrección-- de errores en el proceso.

2.2 En la criptografía cuántica

En contra partida, el teorema de no clonado es esencial para la criptografía cuántica, ya que asegura que es imposible que un tercer observador (espía) copie la señal que las dos partes amigas se intercambian entre si. Así, pues, si el emisor del mensaje cifrado se asegura que cada bit cuántico se envía tan sólo una vez (una sola copia del sistema cuántico que transporta el mensaje), la criptografía cuántica es infalible.

2.3 Sobre las paradojas de la mecánica cuántica

De forma más fundamental, el teorema de no clonado impide la transmisión de señales a velocidad mayor de la velocidad de la luz. Para entender esta afirmación, supongamos que el teorema de no clonado es falso. Consideramos dos electrones, por ejemplo, muy separados entre si y con un estado entrelazado. Si un emisor situado en las cercanías de uno de estos estados decide realizar una medida colapsando la función de onda de todo el conjunto mediante un determinado operador, el receptor (situado en las cercanías del segundo electrón) puede conocer qué operador ha utilizado el emisor (transmitiéndole, pues, información), simplemente realizando un análisis estadístico sobre una gran cantidad de copias del estado sin colapsar.

No obstante, este protocolo no es factible ya que, por el teorema de no clonado, el receptor no puede copiar el estado de su electrón sin colapsar el estado.