Física Cuántica
pod
Date: Septiembre - Octubre del 2001
Introducción
Los apuntes recogidos en el presente documento corresponden al temario de la asignatura de tercer curso (finales del primer ciclo) Física Quàntica de la Facultad de Física de la Universidad de Barcelona. Se tratan en primer lugar los grandes hechos experimentales que llevaron a la revolución que la mecánica cuántica supuso en la concepción de nuestro universo, pasando posteriormente a exponer brevemente los principales métodos de cálculo en que se basa la física cuántica, sin entrar en detalles abstractos sobre los espacios de Hilbert y la notación de Dirac. Por último, se resuelven algunos ejemplos simples de sistemas cuánticos, como son el caso de pozos unidimensionales y el átomo de hidrógeno. En general, los resultados se incluyen sin demostración.
1. Propiedades corpusculares de la radiación
1.1 Radiación del cuerpo negro
Un cuerpo negro es aquel que absorbe toda la radiación electromagnética que incide en su superficie. El teorema de Kirchoff, que afirma que todo buen emisor es buen un buen absorbente y viceversa, nos asegura que el cuerpo negro es también un emisor perfecto. Se observa que el espectro de emisión del cuerpo negro depende de la temperatura, según una densidad espectral de energía
La densidad total de energía viene dada por
![]() . La radiancia
. La radiancia ![]() , flujo por
unidad de tiempo de energía emitida, se relaciona con la densidad total de energía por
, flujo por
unidad de tiempo de energía emitida, se relaciona con la densidad total de energía por
![]() . La
mismas relaciones son ciertas para la densidad espectral de energía i la radiancia espectral.
. La
mismas relaciones son ciertas para la densidad espectral de energía i la radiancia espectral.
Stefan dedujo que la radiancia se relaciona con la temperatura según
![]() , donde
, donde
![]() es la constante de Stefan-Boltzmann. Wien dedujo también que
es la constante de Stefan-Boltzmann. Wien dedujo también que
![]() , de donde se deduce la ley del desplazamiento, que afirma que la frecuencia donde se
emite el máximo de potencia es proporcional a la temperatura.
, de donde se deduce la ley del desplazamiento, que afirma que la frecuencia donde se
emite el máximo de potencia es proporcional a la temperatura.
Max Plank dedujo experimentalmente la expresión definitiva
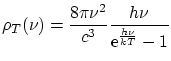
donde
Esta expresión se puede justificar suponiendo que
![]() representa el número de modos en la cavidad con
frecuencia entre
representa el número de modos en la cavidad con
frecuencia entre ![]() y
y
![]() . Si se supone que la energía de los modos sigue la distribución de Boltzmann
discreta
. Si se supone que la energía de los modos sigue la distribución de Boltzmann
discreta
![]() donde
donde
![]() y
y ![]() es una constante de
normalización
es una constante de
normalización
![]() . La energía media de cada modo viene dada por
. La energía media de cada modo viene dada por
Comparando con la ley de Plank, vemos que
El límite
![]() da que la energía media de los modos es
da que la energía media de los modos es ![]() (teorema de equipartición), resultado que
resulta muy errónea a frecuencias altas (catástrofe ultravioleta). Los experimentos confirman la ley de Plank con
(teorema de equipartición), resultado que
resulta muy errónea a frecuencias altas (catástrofe ultravioleta). Los experimentos confirman la ley de Plank con
![]() y la discretización de la energía.
y la discretización de la energía.
1.2 Efecto fotoeléctrico
Basado en la emisión de electrones sobre un metal (cátodo). En 1905 A. Einstein predijo que en este proceso, la luz se comporta como compuesta por partículas (fotones) de energía
Si para desprender el electrón del átomo se necesita una energía ![]() (función de trabajo), la energía cinética del
electrón vendrá dada por
(función de trabajo), la energía cinética del
electrón vendrá dada por
![]() . Esto indica que existe una frecuencia mínima para la cual la energía del
fotón no es suficiente para desprender el electrón,
. Esto indica que existe una frecuencia mínima para la cual la energía del
fotón no es suficiente para desprender el electrón,
![]() .
.
Si entre el ánodo y el cátodo se establece un potencial tal que repele los electrones salientes, llegará un momento que
tan solo los electrones más rápidos podrán llegar al cátodo, se tendrá ![]() . El potencial de corte será, pues
. El potencial de corte será, pues
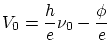
1.2.1 Efecto Compton
El experimento de Compton consiste en la dispersión de rayos X por una lámina fina de granito. Se observa que según el ángulo de dispersión, la longitud de onda de parte de la luz cambia, mientras que parte de la luz permanece con la misma frecuencia. Al aumentar el ángulo de desviación, la diferencia entre ambas partes de la luz aumenta.
Supongamos que el electrón incidente ![]() interacciona con un electrón en reposo, produciendo un nuevo fotón
interacciona con un electrón en reposo, produciendo un nuevo fotón
![]() formando un ángulo
formando un ángulo ![]() , mientras que el electrón retrocede con una energía
cinética
, mientras que el electrón retrocede con una energía
cinética ![]() en un ángulo
en un ángulo ![]() respecto la dirección de incidencia.
respecto la dirección de incidencia.
La conservación de la energía relativista, y las dos componentes del momento lineal, obtenemos las ecuaciones
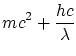 |
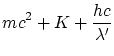 |
||
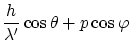 |
|||
| 0 | 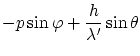 |
Donde
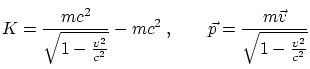
La solución a estas ecuaciones es
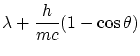 |
|||
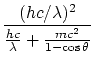 |
|||
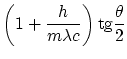 |
Los dos picos se producen por que no solo los electrones desvían los fotones, también los núcleos lo hacen. Como la diferencia de longitud de onda es inversamente proporcional a la masa de la partícula que produce la desviación, y los núcleos son miles de veces mas pesados que los electrones, la diferencia de longitud de onda producida por los núcleos no se aprecia en comparación a la producida por los electrones.
2. Primeros modelos atómicos
2.1 Modelo atómico
La materia se considera formada por entes mínimos que forman los diferentes elementos de la tabla período: átomos, que, conminándose, dan lugar a todas las substancias conocidas. Constituyen pruebas a favor de este modelo la pila de Volta (1745-1827) i la electrólisis del NaCl (Faraday, 1791-1867).Se consideraba que los átomos estaban formada por una nube cargada positivamente, en la cual se incrustan electrones, haciendo neutro el átomo (modelo pastel de pasas).
2.2 Modelo de Rutherford
Rutherford realizó un experimento de dispersión de partículas
Rutherford supuso, entonces, que las partículas ![]() eran dispersadas por otras partículas positivas, siguiendo la
ley de Coulom
eran dispersadas por otras partículas positivas, siguiendo la
ley de Coulom
![]() . Según la mecánica, la trayectoria debe ser una hipérbola, recorrida de forma que
la energía y el momento angular se mantienen constantes. Si
. Según la mecánica, la trayectoria debe ser una hipérbola, recorrida de forma que
la energía y el momento angular se mantienen constantes. Si ![]() es el parámetro de impacto, el momento angular se puede
escribir como
es el parámetro de impacto, el momento angular se puede
escribir como
![]() donde
donde ![]() es la velocidad en el infinito. Igualmente, la energía se puede escribir
es la velocidad en el infinito. Igualmente, la energía se puede escribir
![]() . Se puede demostrar que el ángulo
. Se puede demostrar que el ángulo ![]() de dispersión (ángulo entre las dos asíntotas) viene
dado por
de dispersión (ángulo entre las dos asíntotas) viene
dado por
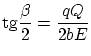
Sea ![]() el número de partículas
el número de partículas ![]() que inciden por
que inciden por
![]() ,
,
![]() el número de partículas que
salen dispersadas por cada átomo por ángulo sólido. El ángulo sólido que ocupa el detector de partículas
el número de partículas que
salen dispersadas por cada átomo por ángulo sólido. El ángulo sólido que ocupa el detector de partículas ![]() a la
salida, se traduce en que recoge las partículas que vienen con un intervalo de parámetros de impacto al rededor de
a la
salida, se traduce en que recoge las partículas que vienen con un intervalo de parámetros de impacto al rededor de ![]() .
Por tanto
.
Por tanto
![]() será el número de partículas que pasan en ese intervalo, es decir, que pasan por la
superficie
será el número de partículas que pasan en ese intervalo, es decir, que pasan por la
superficie
![]() . Por tanto
. Por tanto
Si aplicamos la expresión del ángulo de dispersión, tenemos
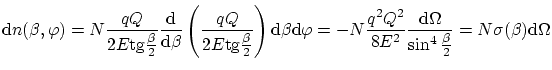
donde
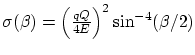 se conoce como
sección eficaz.
se conoce como
sección eficaz.
Ajustando los parámetros de la sección eficaz, Rutherford podía saber la carga del núcleo. Encontró que la carga era
siempre un múltiplo entero de la carga del electrón,
![]() , donde
, donde ![]() coincidía con el número del elemento en la
tabla de Mendeleiev, dando significado al número atómico.
coincidía con el número del elemento en la
tabla de Mendeleiev, dando significado al número atómico.
Rutherford encontró que su modelo explicaba muy bien los resultados para diversos materiales. Por lo tanto, los átomos debían estar compuestos de un núcleo positivo, y los electrones al rededor de él. Para medir el tamaño del núcleo, aumentó la energía hasta que pudieran traspasar totalmente la barrera repulsiva del núcleo,
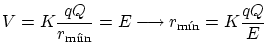
Obtuvo que los núcleos eran cuatro ordenes de magnitud más pequeños que el átomo en si.
Como el modelo funciona correctamente, el electrón ha de estar lejos del núcleo, a la distancia del radio atómico. Para que no colapse a la atracción del núcleo, el electrón por tanto ha de estar girando. Sin embargo, según la electrodinámica, un electrón girando ha de perder energía por radiación y caer sobre el núcleo.
2.3 Modelo de Borh
Para arreglar los problemas del modelo de Rutherford, Borh (1885-1962) introdujo los siguientes postulados:- Los electrones circulan en órbitas circulares estables.
- No hay radiación electromagnética mientras el electrón no cambia de órbita.
- Las órbitas son tales que
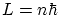 , siendo
, siendo 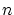 un número natural.
un número natural.
- La radiación se produce cuando el electrón salta de órbita, su frecuencia es
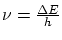 donde
donde
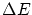 es la diferencia de energía entre ambas órbitas.
es la diferencia de energía entre ambas órbitas.
Del tercer postulado se deducen los radios de las orbitas posibles
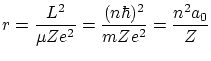
donde
Según la mecánica, la energía de una órbita de este tipo es
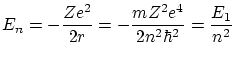
donde
En realizar una transición de orbita, se emite un fotón de frecuencia
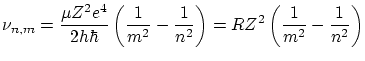
donde
2.4 Experimento de Franck-Hertz
En el experimento de Franck-Hertz se lanzan electrones desde un cátodo a una cavidad, llena de vapor de Hg (la cantidad de Hg se controla a partir de la temperatura). A partir de cierto punto, se establece un potencial de frenado entre el ánodo y un electrodo en forma de rejilla. Si el potencial acelerador de los electrones (entre el cátodo y la rejilla) es suficientemente grande, éstos llegaran al ánodo y establecerán cierta corriente.Sin embargo, si los electrones van demasiado rápidos, provocaran colisiones con los átomos de mercurio, siendo frenados y excitando los electrones del Hg. Si continuamos aumentando el potencial acelerador, aunque se los electrones se frenen por los átomos de mercurio, volverán a acelerarse y de nuevo podrán provocar corriente entre la rejilla y el ánodo. De esta forma, conforme aumentamos el potencial acelerador, la corriente va aumentando, disminuyendo bruscamente en el momento que los electrones son capaces de excitar el mercurio.
Por otra parte, los átomos de mercurio excitados realizaran la transición de relajación en un tiempo
![]() , emitiendo luz de acuerdo con el modelo de Borh. Esta radiación, efectivamente observada, confirma los
postulados de Borh.
, emitiendo luz de acuerdo con el modelo de Borh. Esta radiación, efectivamente observada, confirma los
postulados de Borh.
En el caso del mercurio, los saltos de corriente bruscos se producen a intervalos de
![]() , energía que corresponde
a la de ionización del mercurio. Por otra parte, la luz emitida tiene una longitud de onda de
, energía que corresponde
a la de ionización del mercurio. Por otra parte, la luz emitida tiene una longitud de onda de
![]() .
.
2.5 Espectro de rayos X
Röntgen descubrió los rayos X en 1895, cuando aceleraba electrones emitidos por un cátodo mediante un potencial del orden de
El espectro de los rayos X tiene un fondo, causado por la radiación de frenado, conocida de la electrodinámica, que se
genera cuando los electrones son frenados bruscamente al llegar al ánodo. El espectro se termina el una longitud de
onda ![]() , que se corresponde con la energía cinética máxima de los electrones, que no depende del material.
, que se corresponde con la energía cinética máxima de los electrones, que no depende del material.
Sin embargo, aparecen dos líneas de emisión muy pronunciadas ![]() i
i ![]() , que no parecían tener explicación.
, que no parecían tener explicación.
Por otra parte, si se hace incidir el rayo X sobre el mismo material del ánodo que lo ha generado, se observa un espectro de absorción que crece según la longitud de onda, dando un salto en dos posiciones que, además, no coinciden con las líneas de emisión.
Se cree que los electrones que inciden sobre el átomo ionizan los electrones de las órbitas mas profundas. Los
siguientes electrones del átomo van rápidamente a ocupar los espacios libres. La línea ![]() se origina por los
electrones del segundo nivel que van a ocupar el lugar perdido en el nivel fundamental, mientras que la línea
se origina por los
electrones del segundo nivel que van a ocupar el lugar perdido en el nivel fundamental, mientras que la línea ![]() se origina cuando son los del segundo nivel los que bajan. Por otra parte, no se pueden absorber los fotones de estas
líneas ya que, cuando inciden a un átomo en reposo, este tiene el segundo y el tercer nivel completamente llenos.
se origina cuando son los del segundo nivel los que bajan. Por otra parte, no se pueden absorber los fotones de estas
líneas ya que, cuando inciden a un átomo en reposo, este tiene el segundo y el tercer nivel completamente llenos.
Moseley encontró una ley que predice la longitud de onda de la línea ![]()
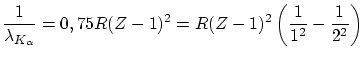
Esta ecuación recuerda la fórmula de Borh, donde se ha apantallado una carga
2.6 Sommerfeld
Observando que las líneas de los espectros están desdobladas, Sommerfeld decidió extender el modelo de Borh incluyendo órbitas elípticas. Aplicando las bien conocidas leyes de la mecánica clásica, obtuvo ya tres de los números cuánticos: uno relaciona con la energía
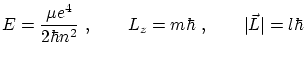
donde
La cuantización de una componente del momento angular se traduce en la cuantización de la orientación de las órbitas: no pueden orientarse en cualquier dirección. Puesto que la elección de el eje Z es propia del observador, debe introducirse en el átomo externamente, por ejemplo mediante un campo magnético. Los electrones, si fueran libres, se colocarían en órbitas perpendiculares al campo, pero dada la cuantificación de Sommerfeld no todos pueden conseguirlo. Por lo tanto, según la orientación, los niveles se desdoblan. Esto se conoce como efecto Zeeman, y está comprobado experimentalmente.
Las predicciones cuantitativas del modelo de Sommerfeld funcionaban parcialmente tan solo en el átomo de hidrógeno.
3. Propiedades ondulatorias de la materia
3.1 Hipótesis de Luis de Broglie
Hasta ahora, hemos visto propiedades corpusculares de la radiación. Vítor Luis de Broglie se atrevió a formular la hipótesis complementaria: las partículas deben comportarse también como ondas. De Broglie supuso que las mismas relaciones entre la energía, momento, longitud de onda y frecuencia válidas para los fotones deberían valer también para otro tipo de partículas, es decir
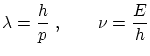
Según esta hipótesis, la única manera de confinar una onda sin que esta desaparezca es que se sitúe en una onda estacionaria. Por lo tanto, cuando un electrón ligado a un átomo, debe formar una onda estacionaria, en la cual la longitud de la órbita ha de ser un múltiplo de la longitud de onda
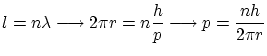
Si la órbita es circular se cumple
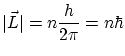
ecuación que coincide con la hipótesis cuántica de Borh.
3.2 Principio de incertidumbre de Heisemberg
Recordemos la definición de la transformada de Fourier, directa e inversa
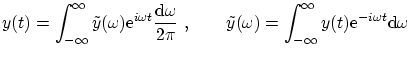
Dado que una onda no puede ser de infinita longitud (como suponemos idealmente), no puede nunca ser realmente monocromática. Supongamos una onda del tipo
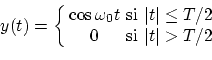
El espectro de frecuencias vendrá dado por la transformada de Fourier
![$\displaystyle \tilde{y}(\omega) =
\frac{T}{2}\left[ \frac{\sin(\omega - \omega_...
...c{\sin(\omega +
\omega_0) \frac{T}{2}}{(\omega + \omega_0)\frac{T}{2}} \right] $](img99.png)
El espectro de frecuencias presenta dos picos (simétricos respecto del origen) al rededor de
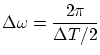
donde
Según la hipótesis de Plank y Einstein
Este tipo de relaciones es habitual cuando se trabaja con variables conjugadas según una transformada de Fourier. En general, el producto de las desviaciones tendrá siempre un valor mínimo. Esto se conoce como principio de incertidumbre de Heisemberg, e implica que el valor de dos cantidades conjugadas según una transformación de Fourier no pueden conocerse con precisión arbitraria simultáneamente. Los ejemplos más habituales son
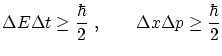
El principio de indeterminación de energía y tiempo implica que, como los fotones emitidos en una transición no pueden
ser indefinidos, su duración temporal será finita (los niveles se desexcitan en
![]() ) y la indeterminación en la
energía no será nula. Si la energía de los fotones no esta determinada, tampoco lo estará la energía de los niveles.
Dicho de otra manera, si la energía de los niveles no esta perfectamente determinada, no pueden ser estables.
) y la indeterminación en la
energía no será nula. Si la energía de los fotones no esta determinada, tampoco lo estará la energía de los niveles.
Dicho de otra manera, si la energía de los niveles no esta perfectamente determinada, no pueden ser estables.
4. Ecuación de Schödinger
4.1 Introducción a la Ecuación de Schödinger
De acuerdo con De Broglie, si los electrones se comportan como ondas estacionarias, debe existir una ecuación de ondas de modos normales. Suponiendo que los modos normales son análogos a los de una cuerda, la ecuación debe ser del tipo
Donde el número de ondas cumple
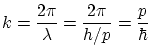
Por otra parte, podemos escribir el momento lineal
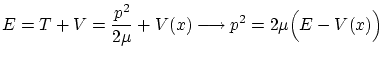
Con lo que nos queda la ecuación de Schödinger independiente del tiempo:
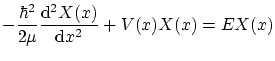
Del mismo modo que en el caso de la cuerda, la ecuación de modos debería poder deducirse por separación de variables de
una ecuación general, que no contuviera las cantidades de separación cuantizadas (en este caso, la energía). Si
suponemos que las ondas de electrones vienen definidas por una función de onda del tipo
![]() , la
ecuación general hallada por Schödinger (y cuya validez viene tan solo justificada experimentalmente, ya que no es la
única ecuación que da lugar a la ecuación de modos separada) es
, la
ecuación general hallada por Schödinger (y cuya validez viene tan solo justificada experimentalmente, ya que no es la
única ecuación que da lugar a la ecuación de modos separada) es
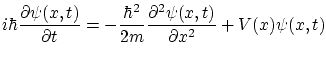
El significado de la función de onda ha sido cuestionado por muchos físicos. La interpretación ortodoxa más comúnmente
aceptada es que la cantidad
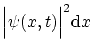 representa la probabilidad de encontrar la partícula entre
la posición
representa la probabilidad de encontrar la partícula entre
la posición ![]() y
y
![]() en el instante
en el instante ![]() . Es decir, la magnitud
. Es decir, la magnitud
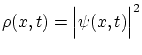 actúa como
una densidad de probabilidad, y por tanto deberá cumplir la condición de normalización
actúa como
una densidad de probabilidad, y por tanto deberá cumplir la condición de normalización
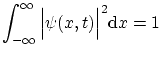
Para obtener de nuevo la ecuación de modos, podemos suponer que la dependencia del tiempo es oscilatoria, es decir
con lo que la distribución de probabilidad queda como
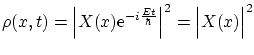
4.2 Espectro de energía
Podemos entender la ecuación de Schödinger como una ecuación de valores propios para un operador diferencial. En este caso, los valores propios son los diferentes niveles de energía permitidos, por lo que el operador diferencial está asociado a la magnitud observable ``energía''.
Según esta filosofía, cada magnitud física ![]() tendrá asociada un operador diferencial
tendrá asociada un operador diferencial ![]() tal que sus valores propios
son los valores permitidos de la magnitud,
tal que sus valores propios
son los valores permitidos de la magnitud,
Dado que el momento lineal de una partícula se puede escribir
![]() , debemos hallar un operador
que al ser aplicado a una función de onda nos de un valor propio
, debemos hallar un operador
que al ser aplicado a una función de onda nos de un valor propio
![]() . El operador encontrado por Schödinger
(avalado por la experimentación) es
. El operador encontrado por Schödinger
(avalado por la experimentación) es
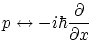
con lo que el operador asociado a la energía será
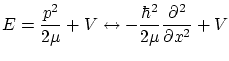
Además, según los teoremas generales para ecuaciones de valores propios, si tenemos dos funciones de onda ![]() i
i
![]() asociadas a energías (valores propios) diferentes, se tiene la condición de ortogonalidad
asociadas a energías (valores propios) diferentes, se tiene la condición de ortogonalidad
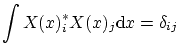
4.3 Pozo de potencial
Un pozo de potencial esta caracterizado por una función potencial del tipo
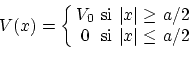
El espacio queda dividido en tres zonas, (I) izquierda del pozo, (II) interior del pozo y (III) derecha del pozo. La
solución a la ecuación de Schödinger en cada zona, si consideramos estados ligados con ![]() , vienen dadas por
, vienen dadas por
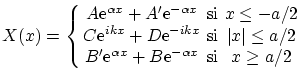
donde
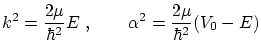
En un estado ligado, si la partícula no debe poder escapar totalmente del pozo, por lo que las condiciones de contorno son
Estas condiciones nos fijan
Como tanto el potencial como la ecuación tienen simetría de paridad, también la tendrán las soluciones,
![]() , y existirán soluciones pares y impares.
, y existirán soluciones pares y impares.
Las soluciones pares serán
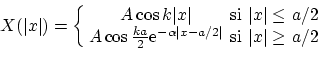
donde la constante de normalización
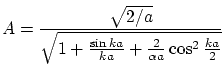
Las condiciones de continuidad exigen
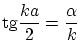
ecuación que determinará los valores posibles de la energía.
Por otra parte, las soluciones impares serán
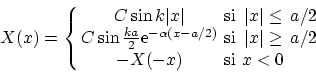
donde la constante de normalización
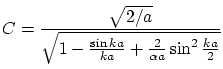
Las condiciones de suavidad ahora nos imponen la ley de cuantización
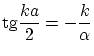
Se puede ver que siempre existe al menos una solución (par). Además, las soluciones están ordenadas, de menor a mayor energía, siguiendo siempre la secuencia par, impar, par...
Si definimos los parámetros del pozo
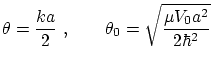
podemos escribir el potencial y la energía de cada modo según
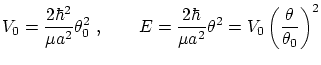
mientras que las condiciones de cuantización, que nos permitirán conocer los valores posibles de
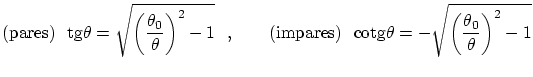
4.3.1 Oscilador armónico
El potencial de oscilador armónico se puede escribir
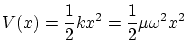
con lo que la ecuación de Schödinger independiente del tiempo es
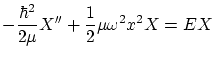
Para poder escribir la ecuación de forma adimensional, definimos los parámetros
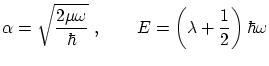
si hacemos el cambio de variables
![$\displaystyle \left[ \frac{\ensuremath{\mathrm{d}}^2}{\ensuremath{\mathrm{d}}\xi^2} + \left(
\lambda + \frac{1}{2} - \frac{1}{4} \xi^2 \right) \right] X = 0 $](img156.png)
De nuevo, las condiciones de contorno son
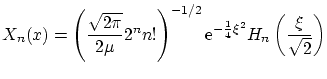
donde
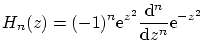
y los niveles de energía permitidos son
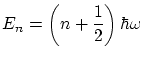
4.4 Estados no ligados
Volviendo al potencial de pozo, que ocurre si la energía es mayor que la barrera de potencial? En este caso, la solución puede escribirse como
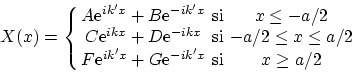
donde
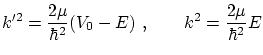
Si todas las partículas son emitidas desde la izquierda, no existe ninguna fuente en el lugar positivo de donde pueden
venir partículas en dirección regresiva, es decir ![]() . Las condiciones de suavidad nos permiten hallar las
constantes las demás constantes en función del flujo de partículas incidentes
. Las condiciones de suavidad nos permiten hallar las
constantes las demás constantes en función del flujo de partículas incidentes ![]() . En realidad, tan solo nos interesan
las constantes
. En realidad, tan solo nos interesan
las constantes ![]() i
i ![]() , que resultan ser
, que resultan ser
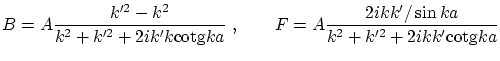
El coeficiente de transmisión de partículas viene dado por
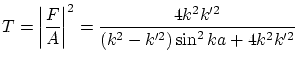
Mientras que el coeficiente de reflexión resulta ser
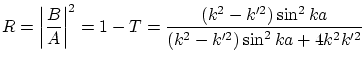
El coeficiente de reflexión se anula si
es decir, si la longitud del pozo es un múltiplo de la longitud de onda der la partícula en cuestión.
4.5 Barrera de potencial
Podemos modelizar una barrera de potencial cuadrada por la función
donde
Si suponemos ![]() y procediendo de manera similar al apartado anterior, obtenemos el coeficiente de transmisión
y procediendo de manera similar al apartado anterior, obtenemos el coeficiente de transmisión
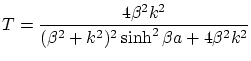
donde
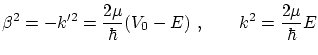
Vemos que en ningún caso podemos obtener
En el caso que ![]() , obtenemos
, obtenemos
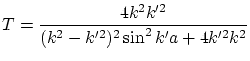
5. Átomos con un electrón
5.1 Ecuación de Schödinger en tres dimensiones
Recordemos que, en una dimensión, el operador asociado a la energía se define a partir del operador del momento lineal, para poder escribir la ecuación de Schödinger debemos extender la definición del operador de momento lineal a tres dimensiones.Puesto que en una dimensión, el operador del momento lineal se define como una derivación respecto la variable, resulta lógico escribir el momento lineal en tres dimensiones como
y, por lo tanto, la ecuación de Schödinger en varias dimensiones se escribe como
![$\displaystyle \left[ - \frac{\hbar^2}{2\mu} \nabla^2 +
V( {\vec r} ) \right] X( {\vec r} ) = E X( {\vec r} ) $](img181.png)
Por otra parte, en tres dimensiones también cabe definir el momento angular
![]() . De la misma forma
que anteriormente, podemos encontrar los operadores asociados a cada una de sus componentes, que en coordenadas
esféricas
. De la misma forma
que anteriormente, podemos encontrar los operadores asociados a cada una de sus componentes, que en coordenadas
esféricas
![]() se escriben
se escriben
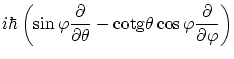 |
|||
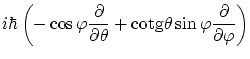 |
|||
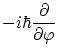 |
observemos que
![$\displaystyle L^2 = - \hbar
\left[ \frac{1}{\sin^2\theta} \frac{\partial }{\par...
...\right) + \frac{1}{\sin^2\theta}
\frac{\partial ^2}{\partial \theta^2} \right] $](img192.png)
5.2 Potenciales radiales
Entendemos por potencial radial aquél que tan solo depende de la distancia
![$\displaystyle \nabla^2 = \frac{1}{r}
\frac{\partial ^2}{\partial r^2} r + \frac...
...\right)
+\frac{1}{\sin^2\theta} \frac{\partial ^2}{\partial \varphi^2} \right] $](img193.png)
Vemos que la expresión anterior es la misma que la del momento angular, por lo que podemos escribir
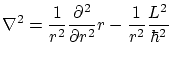
Si suponemos una separación de variables de la ecuación de Schödinger del tipo
obtenemos la ecuación separada para los ángulos
que nos indica la cuantización de
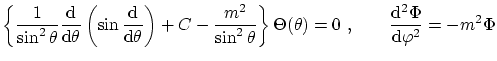
La última de estas ecuaciones tiene por solución general
Aplicando el operador
es decir, la componente
Las soluciones a estas ecuaciones para
![]() se conocen como armónicos esféricos, que tan solo tienen
sentido para los valores
se conocen como armónicos esféricos, que tan solo tienen
sentido para los valores
![]() , con
, con
![]() entero, i para
entero, i para
![]() . Los
armónicos esféricos se pueden escribir como
. Los
armónicos esféricos se pueden escribir como
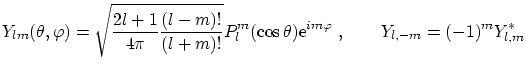
donde
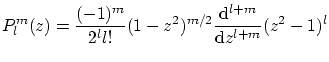
La condición de ortogonalidad de los armónicos esféricos es
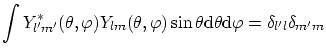
Por lo tanto, para todos los los potenciales radiales, tenemos cuantizado el modulo del momento angular y también una de sus componentes,
como
5.3 Átomos con un electrón
En un átomo con un solo electrón, no existe apantallamiento de la carga del núcleo y el potencial viene dado por
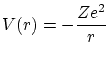
Si suponemos una separación de variables del tipo
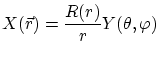
la ecuación radial es
![$\displaystyle \left[ - \frac{\hbar^2}{2\mu} \frac{\ensuremath{\mathrm{d}}^2}{\ensuremath{\mathrm{d}}r^2} + V(R) + \frac{l(l+1)}{2\mu r^2}
\right] R(r) = E R(r) $](img215.png)
Para escribir la ecuación en forma adimensional, definimos
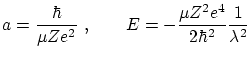
y realizamos el cambio de variable
![$\displaystyle \left[ \frac{\ensuremath{\mathrm{d}}^2}{\ensuremath{\mathrm{d}}\x...
... - \frac{l(l+1)}{\xi^2} + \frac{2}{\xi} - \frac{1}{\lambda^2}
\right] R(r) = 0 $](img218.png)
Las condiciones de contorno deben ser
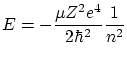
La solución, normalizada, resulta ser
![$\displaystyle R_{nl}(r) = \sqrt{ \frac{(n-l-1)!}{2n a [(n+l)!]^3} \left( \frac{...
...)^{2l+3} } \xi^{l+1} \mathcal{L}^{2l+1}_{n+l} \ensuremath{\mathrm{e}^{-\xi/n}} $](img222.png)
donde
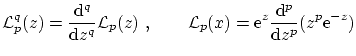
mientras que la condición de ortogonalidad resulta ser la acostumbrada
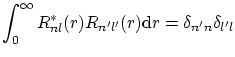
En resumen, hemos encontrado tres numeros cuánticos: el número cuántico principal (de Borh)
![]() , que
influye a la energía; el número cuántico secundario
, que
influye a la energía; el número cuántico secundario
![]() , que influye en el modulo del momento angular;
y el tercer número cuántico
, que influye en el modulo del momento angular;
y el tercer número cuántico
![]() , que influye a la componente
, que influye a la componente ![]() del momento angular.
del momento angular.
Como tan solo el número cuántico principal influye en la energía, varios cada nivel energético constará de diversos subniveles, es decir, la energía está degenerada. La degeneración vendrá dada por