Secciones Destacados Apuntes

Apuntes Secciones Por rama Por nivel Por tipo Apuntes Otros

Búsqueda

Bájatelo

Física general de fluidos

por h[e]rtz

Date: Verano 2003

1. Hidrostática. Principio de Pascal. Principio de Arquímedes.

Conceptos básicos de hidrodinámica:

$\bullet$ Una importante propiedad de una sustancia es la densidad, que la definiremos como el cociente de la masa y el volumen,

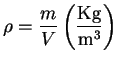
$\displaystyle \rho = \frac{m}{V} \left( \frac{\mathrm{Kg}}{\mathrm{m^3}} \right)$

En la mayoría de los materiales, incluida el agua, las densidades varían con la temperatura.
Una unidad de volumen muy utilizada es el litro (L):

$\displaystyle 1 \mathrm{L = 10^3cm^3 = 10^{-3} m^3 }$

$\bullet$ Cuando un cuerpo se sumerge en un fluido, éste ejerce una fuerza perpendicular a la superficie del cuerpo en cada punto de la superficie. Definiremos presión del fluido como esta fuerza por unidad de área

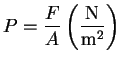
$\displaystyle P = \frac{F}{A} \left( \frac{\mathrm{N}}{\mathrm{m^2}} \right)$

La unidad en el SI es el Newton por metro cuadrado, que recibe el nombre de Pascal:

$\displaystyle 1 \mathrm{Pa = 1N/m^2 }$

Una de la unidades también común cuando se habla de presión, es la atmósfera (atm), que es aproximadamente la presión del aire a nivel del mar.

$\displaystyle \mathrm{1 atm = 101,325 KPa = 14,70 Ib/pulg^2 = 760 mm Hg}$

Un fluido que presiona contra un cuerpo, tiende a comprimirlo.
El cociente entre el cambio de presión y la disminución relativa al volumen $(\Delta V /V)$ se denomina módulo de compresibilidad

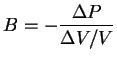
$\displaystyle B = - \frac{\Delta P} {\Delta V/V}$

Algunos valores aproximados del módulo de compresibilidad de varios materiales:

Diamante: 620
Acero: 160
cobre: 140
Aluminio: 70
Plomo: 7,7

$\bullet$ Principio de Pascal: Toda presión aplicada en un punto del fluido se trasmite a todos los puntos del fluido.

Ejemplo, prensa hidráulica o elevador hidráulico.

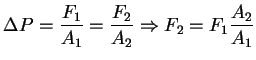
$\displaystyle \Delta P = \frac{F_1}{A_1} = \frac{F_2}{A_2} \Rightarrow F_2 = F_1 \frac{A_2}{A_1}$

Donde una fuerza ejercida sobre el émbolo o pistón pequeño produce una variación de presión que se trasmite por el líquido hasta el émbolo grande. Como las presiones en los pistones grande y pequeño son iguales, las fuerzas correspondientes cumplen la relación Como el área del pistón grande es mucho mayor que el del pistón pequeño, la fuerza sobre el pistón grande es mucho mayor que

$\bullet$ Ecuación fundamental de la hidrostática
Supongamos dos alturas y en un fluido; la ecuación fundamental de la hidrostática es

$\displaystyle P(z) + \rho g z = P(H) + \rho g H$

para $\rho$ constante, y donde

es el valor de la gravedad,

las correspondientes alturas. Una expresión más general de esta ecuación es

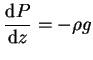
$\displaystyle \frac{\mathrm{d}P}{\mathrm{d}z} = - \rho g$

$\bullet$ Principio de Arquímedes (250 a.C.)
Todo cuerpo parcial o totalmente sumergido en un fluido, experimenta un empuje ascensional igual al peso del fluido desplazado.

Consecuencia del principio fundamental de la hidrostática.

Este principio también explica por qué un objeto sumergido en el agua, su peso aparente es menor que si lo pesamos en el aire.

En la deducción de este principio, la fuerza neta de la presión solo depende de la posición (geometría del objeto y de la profundidad). En el caso del fluido dentro del fluido (equilibrio), la fuerza neta de la presión tiene que ser igual al peso del fluido contenido en el volumen considerado.

2. Tensión superficial. Capilaridad. Ley de Jurin

$\bullet$ Tensión superficial

Hacer pasar una molécula del interior de un líquido a la superficie del líquido cuesta energía.

En el interior del líquido, la molécula está rodeada de otras moléculas en todas las direcciones, de manera en que la fuerza neta es nula.

Cerca de la superficie, la molécula solo está rodeada parcialmente de otras moléculas del líquido, de manera que esto provoca una fuerza atractiva neta hacia dentro del líquido.

Para extraer la molécula, hace falta hacer un trabajo (tensión superficial, si la llevamos a la superficie; evaporación, la extraemos del todo).

Sea $\delta$ el alcance de la fuerza, y la fuerza molecular mediana, el trabajo será igual al producto de estos,

$\displaystyle W = F \delta$

Ampliar el área superficial de un líquido, también cuesta energía

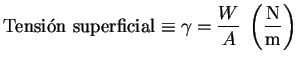
$\displaystyle \textrm{Tensi� superficial} \equiv \gamma = \frac{W}{A} \; \left( \frac{\mathrm{N}}{\mathrm{m}}\right)$

donde

es el trabajo y

el área.

Ejemplos de valores de tensión superficial en diferentes fluidos

Agua a 273 K: 75,5 N/m
Agua a 373 K: 58,9 N/m
Etanol: 22,3 N/m
Aceite de oliva: 32,0 N/m
Mercurio: 465,0 N/m

Consecuencia:

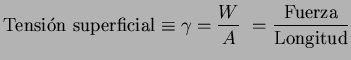
$\displaystyle \textrm{Tensi� superficial} \equiv \gamma = \frac{W}{A} = \frac{\mathrm{Fuerza}}{\mathrm{Longitud}}$

Observaciones: Insectos que caminan sobre el agua, detergentes (la reducción de la tensión superficial mejora el rendimiento de limpieza).

Ley de Laplace: diferencia de presiones entre el exterior y el interior de una gota (o un depósito).
La tensión superficial aumenta la presión dentro de una gota del líquido. La presión interna P, que balancea la fuerza de tensión superficial de una pequeña gota esférica de radio r

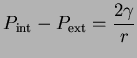
$\displaystyle P_{\textrm{int}} - P_{\textrm{ext}} = \frac{2 \gamma}{r}$

Trabajo necesario para atomizar una masa de líquido

$\displaystyle W = \gamma ( A_{\textrm{final}}- A_{\textrm{inicial}} )$

$\bullet$ Fuerzas cohesivas y adhesivas. Capilaridad
Los líquidos poseen las propiedades de cohesión y adhesión debido a la atracción molecular. Debido a la propiedad de cohesión, los líquidos pueden resistir pequeñas fuerzas de tensión en la interfase entre el líquido y aire, conocida como tensión superficial.
La cohesión permite al líquido resistir esfuerzos de tracción, mientras que la adhesión permite que se adhiera a otros cuerpos.

Si las moléculas líquidas tienen mayor adhesión que cohesión, entonces el líquido se pega a las paredes del recipiente con el cual está en contacto, resultando en un aumento (elevación) de la capilaridad de la superficie del líquido; un predominio de la cohesión causa por el contrario una depresión de la capilaridad.

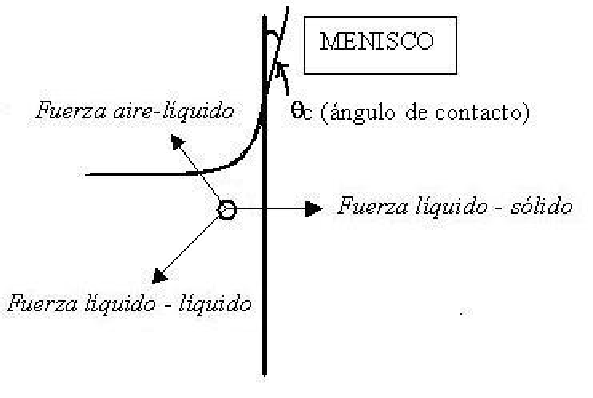
Esta imagen del menisco nos muestra, las fuerzas que actúan sobre una molécula en un fluido contenido en un recipiente, vemos que las tres fuerzas que actúan son: la fuerza de líquido - sólido, la fuerza del aire - líquido, y la fuerza de líquido - líquido.

$\includegraphics{fuerzasdecohesion}$

El ángulo de contacto $\theta_c$ (depende exclusivamente de las fuerzas adhesivas y cohesivas).
Ejemplos: ángulo de contacto de Agua-vidrio: 0^o, ángulo de contacto de Mercurio-vidrio: 140^o.

$\bullet$ Para estudiar el ascenso o el descenso de líquidos en conductos finos, nos preguntaremos primeramente a que distancia puede subir o bajar el líquido. Analicemos las fuerzas que intervienen arriba y abajo

$\displaystyle F_{\textrm{arriba}} = 2 \pi r \gamma \cos \theta_c$

$\displaystyle F_{\textrm{abajo}} = \textrm{Peso} = \pi r^2 h \rho g$

en igualar las dos fuerzas obtenemos

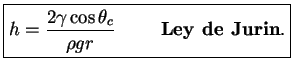
$\displaystyle \boxed{h = \frac{2 \gamma \cos \theta_c}{\rho g r} \hspace{1cm} \textbf{Ley de Jurin}.}$

3. Hidrodinámica. Ecuación de continuidad. Fluido perfecto. Ecuación de Bernoulli.

Para el movimiento de fluidos supondremos fluidos incompresibles, consideraremos dos variables: velocidad y presión, y conoceremos la geometría del conducto.

Necesitaremos dos ecuaciones para describir el movimiento de los fluidos bajo las condiciones comentadas anteriormente
$\diamond$ Ecuación de continuidad (conservación de la masa).
$\diamond$ Ecuación de Bernoulli (conservación de la energía).

$\bullet$ Ecuación de continuidad y conservación de la masa.

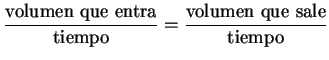
$\displaystyle \frac{\textrm{volumen que entra}}{\textrm{tiempo}} = \frac{\textrm{volumen que sale}}{\textrm{tiempo}}$

Volumen que entra o sale en un intervalo de tiempo $\textrm{d}t$

$\displaystyle \textrm{d}V_{\mathrm{entra}} = v_1 \textrm{d}t A_1 , \hspace{1cm} \textrm{d}V_{\mathrm{sale}} = v_2 \textrm{d}t A_2 ,$

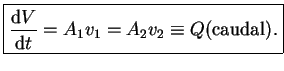
$\displaystyle \boxed{ \frac{\textrm{d}V}{\textrm{d}t}= A_1 v_1 = A_2 v_2 \equiv Q (\textrm{caudal}).}$

Podemos observar que si

aumenta $\Rightarrow v$ disminuye.

$\bullet$ Ecuación de Bernoulli
La ecuación de Bernoulli solo vale para fluidos perfectos, es decir, fluidos sin viscosidad.

Ejemplo de la ecuación de Bernoulli en un conducto horizontal y de sección constante.

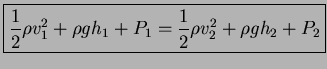
$\displaystyle \boxed{\frac{1}{2} \rho v_1^2 + \rho g h_1 + P_1 = \frac{1}{2} \rho v_2^2 + \rho g h_2 + P_2}$

y otra ecuación más general

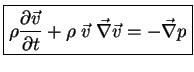
$\displaystyle \boxed{\rho \frac{\partial \vec v}{\partial t} + \rho \; \vec v \; \vec \nabla \vec v = - \vec \nabla p}$

Nótese que cuando la velocidad es 0, recuperamos la ecuación fundamental de la hidrostática.

$\diamond$ Si el área es constate (velocidad constante) y altura constante $\Rightarrow$ que la presión tendría que ser constante, pero se observa que el fluido pierde presión.
Esto se explica por la presencia de las fuerzas de resisténcia (fuerzas viscosas) que no han estado tenidas en cuenta en la deducción de la ecuación de Bernoulli.

Un buen ejemplo de esto es observar el vuelo de los aviones. En los cuales, si nos fijamos en el ala del avión, veremos que el aire que fluye por encima del ala y el que fluye por debajo del ala tarda el mismo tiempo aunque el espacio recorrido no es el mismo; asi pues, $v_1<v_2 \Rightarrow p_1>p_2$ , por eso se genera una fuerza de sustentación que hace que el ala planee, pero este tema ya lo comentaremos más adelante.

Efecto Venturi: Cuando aumenta la velocidad de un fluido, desciende su presión.

4. Fluido viscoso. Ley de Poiseuille. Número de Reynolds. Turbulencia.

$\bullet$ Ley de Newton de la viscosidad
Fuerzas de viscosidad: fricción interna del fluido.

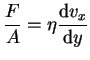
$\displaystyle \frac{F}{A}= \eta \frac{\textrm{d}v_x}{\textrm{d}y}$

donde $\eta$ es el coeficiente de viscosidad que depende del fluido.

No todos los fluidos satisfacen exactamente esta ley (ejemplo: la sangre, el petróleo, suspensiones, pinturas, ...) que son fluidos no newtonianos; y su viscosidad depende del gradiente de la velocidad.

En algunos, la viscosidad disminuye cuando el gradiente de la velocidad aumenta (ejemplo: pinturas, suspensiones, ...)

Aplicaciones: flujo en conductos cilíndricos. Ecuación de Poiseuille

Supongamos un cilindro de radio contenido en otro cilindro de radio y longitud .
Sobre el cilindro considerado actúan las siguientes fuerzas

$\displaystyle \textrm{Presi�} \hspace{2cm} F=\pi r^2 \Delta P$

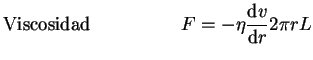
$\displaystyle \textrm{Viscosidad} \hspace{2cm} F= - \eta \frac{\textrm{d}v}{\textrm{d}r} 2 \pi r L$

Igualamos las fuerzas y obtenemos

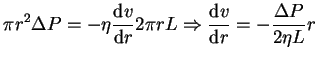
$\displaystyle \pi r^2 \Delta P = - \eta \frac{\textrm{d}v}{\textrm{d}r} 2 \pi r L \Rightarrow \frac{\textrm{d}v}{\textrm{d}r} =- \frac{\Delta P}{2 \eta L} r$

la diferencia de presiones es lo que hace mover el fluido. Aislando tendremos el perfil parabólico de velocidades

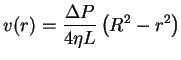
$\displaystyle v(r)= \frac{\Delta P}{4 \eta L} \left( R^2 - r^2 \right)$

Para calcular el caudal utilizaremos esta expresión

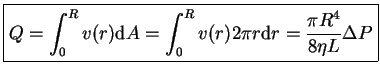
$\displaystyle \boxed{Q=\int_{0}^{R}v(r)\textrm{d}A = \int_{0}^{R} v(r)2 \pi r \textrm{d}r= \frac{\pi R^4}{8 \eta L} \Delta P }$

$\bullet$ Ecuación de Poiseuille(1835)

En función del coeficiente de viscosidad, se puede demostrar que la caída de presión para un flujo estacionario en una longitud de un tubo circular de radio es

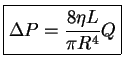
$\displaystyle \boxed{\Delta P = \frac{8 \eta L}{\pi R^4} Q}$

La Ley de Poiseuille se aplica sólo al flujo laminar (no turbulento) de un fluido de viscosidad constante que es independendiente de la velocidad del fluido.

La sangre es un fluido complejo formado por partículas sólidas de diferentes formas suspendidas en un líquido. Los glóbulos rojos de la sangre, por ejemplo, son corpúsculos de forma de disco que están orientados al azar a velocidades bajas pero que resultan orientados a velocidades altas para facilitar el flujo. Así pues, la viscosidad de la sangre disminuye cuando aumenta la velocidad de flujo, de forma que la ley no es estrictamente válida. Sin embargo, dicha ley es una buena aproximación que es muy útil a la hora de obteneter una comprensión cualitativa del flujo sanguíneo.

Analogía con el corriente eléctrico (Ley de Ohm) $\Delta V = R_e I$ .
Importancia del exponente 4 en la regulación del caudal sanguíneo (ya que, pequeñas modificaciones del radio influyen mucho en el caudal).

$\bullet$ Aplicaciones prácticas

Permeabilidad de membranas:
canales cilíndricos de radios y de longitud (grueso de la membrana).

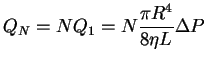
$\displaystyle Q_N = N Q_1 = N \frac{\pi R^4}{8 \eta L} \Delta P$

donde

es el caudal que traviesa la membrana.
En algunas ocasiones, desconocemos

; así que nos hace falta alguna otra ecuación para poder determinar separadamente las dos magnitudes.

Flujo de agua o de petróleo en terrenos

$\displaystyle \boxed{ Q = k \nabla P}\hspace{2cm} \textbf{Ley de Darcy}$

donde

es la permeabilidad del terreno que depende del tipo de roca, arena, sedimento, ...

Potencia necesaria para impulsar un fluido en un conducto

(Ejemplos: Oleoducto, distribución de agua, sistema circulatorio, ...)

$\displaystyle \textrm{Potencia} = \textrm{Fuerza} \times \textrm{velocidad}$

$\displaystyle P = (P_1A_1)v_1 - (P_2 A_2)v_2 = (P_1P_2)A \; v =(\Delta P)Q$

Importante la analogía con el caso eléctrico $P=(\Delta V)I$

$\bullet$ Turbulencia
La aparición de las turbulencias limita la ecuación de Poiseuille como vimos anteriormente.

Hay dos tipos de flujos, el flujo de régimen laminar de carácter suave y ordenado; y el flujo turbulento de caracter irregular y desordenado.

Dentro del fenómeno de la turbulencia se originan muchas colisiones, mucha fricción y un aumento considerable de la resistencia.

$\bullet$ Número de Reynolds
Cuando la velocidad de flujo de un fluido resulta que es suficientemente grande, se rompe el flujo laminar y se establece la turbulencia. La velocidad crítica por encima de la cual el flujo a través de un tubo resulta turbulenta depende de la densidad y de la viscosidad del fluido y del radio del tubo.
El flujo de un fluido puede caracterizarse mediante un número adimensional al que denominamos número de Reynolds $N_{\textrm{R}}$ que se define

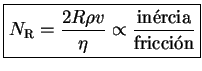
$\displaystyle \boxed{N_{\textrm{R}} = \frac{2 R \rho v}{\eta} \propto \frac{\textrm{in�cia}}{\textrm{fricci�}} }$

Se observa que cuando

$\displaystyle \textrm{\textbf{Nmero de Reynolds}} < 2000 \Rightarrow \textrm{el flujo es laminar}$

$\displaystyle \textrm{\textbf{Nmero de Reynolds}} >3000 \Rightarrow \textrm{el flujo es turbulento}$

Y cuando Número de Reynolds el régimen del flujo puede ser laminar o turbulento.

5. Movimiento de sólidos en fluidos. Ley de Stokes. Resistencia hidrodinámica

Cuando un objeto se mueve en un fluido, existen fuerzas entre el fluido y el objeto que dependen de la velocidad.

Recordemos que $N_{\textrm{R}}= 2 R \rho v / \eta$ , entonces

$\displaystyle \textrm{Si} \; N_{\textrm{R}} « 1 , \hspace{0.5cm} \Rightarrow F \propto v \hspace{0.5cm} \textrm{(Domina la viscosidad)}$

$\displaystyle \textrm{Si} \; N_{\textrm{R}} » 1 , \hspace{0.5cm} \Rightarrow F \propto v^2 \hspace{0.5cm} \textrm {(Domina la turbulencia)}$

$\bullet$ Movimiento de una esfera a $N_{\textrm{R}} « 1$ . Ley de Stokes
El origen de la fuerza es la fricción viscosa.

$\displaystyle F= 6 \pi \eta r v \hspace{1cm} \textrm{\textbf{Ley de Stokes} (1870) }$

el factor $6 \pi$ vale para la esfera, $\eta$ es la viscosidad.

Velocidad de sedimentación
Consideremos esta aplicación para una esfera sumergida en un fluido, entonces las fuerzas que actúan son

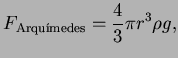
$\displaystyle F_{\textrm{Arqu�edes}} = \frac{4}{3} \pi r^3 \rho g ,$

$\displaystyle F_{\textrm{Stokes}}= 6 \pi \eta r v ,$

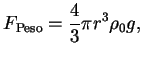
$\displaystyle F_{\textrm{Peso}}= \frac{4}{3}\pi r^3 \rho_0 g ,$

donde $\rho$ es la densidad del fluido, y $\rho_0$ es la densidad del objeto.

Se llega a velocidad constante de sedimentación cuando

$\displaystyle F_{\textrm{Peso}} = F_{\text{Arqu�edes}} + F_{\textrm{Stokes}} ,$

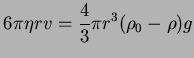
$\displaystyle 6 \pi \eta r v = \frac{4}{3} \pi r^3 (\rho_0-\rho) g$

Y aislando

de la ecuación, tendremos la velocidad de sedimentación

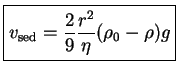
$\displaystyle \boxed{ v_{\textrm{sed}}= \frac{2}{9} \frac{r^2}{\eta} (\rho_0 - \rho) g }$

El mismo caso, pero bajo la acción de una aceleración centrífuga como en el caso de una centrifugación vale

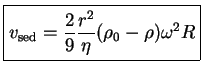
$\displaystyle \boxed{ v_{\textrm{sed}} = \frac{2}{9} \frac{r^2}{\eta} (\rho_0 - \rho) \omega^2 R }$

En este caso podemos observar que $\omega^2 R$ puede ser mucho más grande que

, hasta 100.000 veces más grande! $\Rightarrow$ la velocidad de sedimentación aumenta mucho respecto de la que produciría la gravedad.

Electroforesi: En este caso en lugar de , actúa una fuerza eléctrica debida a un campo eléctrico

$\displaystyle 6 \pi \eta r v = q E \hspace{1.5cm} \textrm{con}\; q \; \textrm{como carga el�trica} ,$

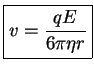
$\displaystyle \boxed{ v=\frac{q E}{6 \pi \eta r} }$

$\bullet$ Movimiento de objetos a $N_{\textrm{R}} » 1$
A medida que va aumentando el $N_{\textrm{R}}$ , aparecen inestabilidades (vórtices), además de haber mucha turbulencia en la zona posterior del objeto.

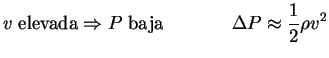
$\displaystyle v \; \textrm{elevada} \Rightarrow P \; \textrm{baja} \hspace{1.5cm} \Delta P \approx \frac{1}{2} \rho v^2$

en este caso se genera una fuerza

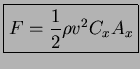
$\displaystyle \boxed{ F= \frac{1}{2} \rho v^2 C_x A_x }$

donde

es la proyección de área frontal, y

el coeficiente de resistencia aerodinámica que depende de la forma del objeto.

De hecho en muchas ocasiones, una de las caracteristicas importantes a la hora de escoger un automóbil es este coeficiente aerodinámico, ya que mientras menor sea su coeficiente, menor será la fuerza de resistencia.
Algunos ejemplos son: Opel Corsa(0,36), Ford Escort (0,38), Audi 100 (0,30), Mercedes 190 (0,33), y los peces desde(0,06) hasta (0,25).

Potencia consumida

$\displaystyle P = F v ,$

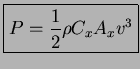
$\displaystyle \boxed{ P= \frac{1}{2} \rho C_x A_x v^3 }$

$\bullet$ Fuerza de sustentación. Potencia de vuelo

$\diamond$ Cuando los objetos son asimétricos, hay una fuerza perpendicular a la velocidad, denominada fuerza de sustentación.

Un buen ejemplo es el ala de los aviones. Son objetos asimétricos, de manera que el flujo del fluido cuando el ala se mueve con velocidad se separa, supongamos que sea el flujo de aire que pasa por la zona de arriba del ala, y la velocidad del flujo del aire que pasa por la parte de abajo del ala.
Como el objeto no es simétrico, y la parte de arriba del ala es mayor (ya que es curbada)que la de abajo, y el tiempo que tardan en recorrer ese espacio es el mismo, tenemos que

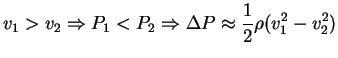
$\displaystyle v_1 > v_2 \Rightarrow P_1 < P_2 \Rightarrow \Delta P \approx \frac{1}{2} \rho (v_1^2 - v_2^2)$

$\displaystyle \Delta P \; A = F$

De manera que la fuerza de resistencia es

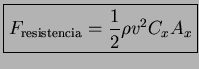
$\displaystyle \boxed{F_{\textrm{resistencia}}=\frac{1}{2} \rho v^2 C_x A_x }$

y la fuerza de sustentación es

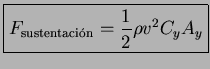
$\displaystyle \boxed{F_{\textrm{sustentaci�}}= \frac{1}{2} \rho v^2 C_y A_y }$

con

coeficientes de resistencia y sustentación correspondientes que dependen de la forma del objeto. Y con

el área de la proyección vertical y horizontal del objeto.

Leyes de escala de velocidad y potencia: túnel de viento
Para simular el vuelo de los aviones y su velocidad, antes se estudia con maquetas de aviones haciendolas pasar por un túnel de viento.
Representemos esto como una maqueta de avión el cual va con una velocidad y que tiene dos alas.
De manera que las fuerzas que actúan son: la fuerza de sustentación de cada ala, y la fuera de resistencia en sentido opuesto al movimiento, y en este caso al de la velocidad .

Nos queda lo siguiente

$\displaystyle mg = F_{\textrm{sustentaci�}}= 2 \frac{1}{2} \rho v^2 C_y A_y \; ,$

y aislando la velocidad de la ecuación

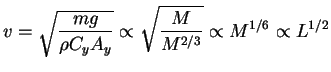
$\displaystyle v= \sqrt{ \frac{mg}{\rho C_y A_y}} \propto \sqrt{\frac{M}{M^{2/3}}} \propto M^{1/6} \propto L^{1/2}$

y para la potencia

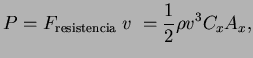
$\displaystyle P = F_{\textrm{resistencia}} \; v \; = \frac{1}{2} \rho v^3 C_x A_x ,$

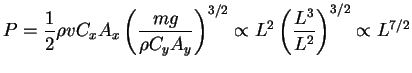
$\displaystyle P=\frac{1}{2} \rho v C_x A_x \left( \frac{mg}{\rho C_y A_y}\right)^{3/2} \propto L^2 \left( \frac{L^3}{L^2}\right)^{3/2} \propto L^{7/2}$

de manera que en aeronáutica, las leyes de escala en la relación maqueta/prototipo seria, por ejemplo

$\displaystyle (1/100) \Rightarrow P_{{prototipo}} = (100)^{7/2} P_{{maqueta}}$

Acceso rápido