Relatividad Especial
Barbol
1 Introducción
La teoría de la relatividad especial fue presentada por Albert Einstein en su trabajo Sobre la electrodinámica de los cuerpos en movimiento, en 1905. El formalismo básico de la teoría ya había sido descubierto un año antes por Poincaré y por Lorentz, aunque Einstein desconocía estos trabajos (y trabajos aún anteriores en los que se utilizaban las transformaciones de Lorentz, incluso antes de que las postulase físico holandés).
El éxito de Einstein consistió en eliminar un gran número de hipótesis hechas por Lorentz hasta reducir la teoría de la relatividad a dos postulados muy simples que parten de la experimentación. Posteriormente, en 1916, Einstein publicó la teoría de la relatividad general, que globaliza todos los hechos físicos y de la que la teoría que se explica aquí es sólo un caso especial (y de ahí el nombre).
1.1 Las primeras sospechas
A finales del siglo XIX la teoría electromagnética había demostrado su vericidad de un modo aplastante. Por otro lado la mecánica de Newton había hecho predicciones válidas siempre que se puso a prueba. Sin embargo, ambas teorías eran incompatibles entre sí: mientras las ecuaciones de Newton eran invariantes de Galileo las ecuaciones de Maxwell resultaron no serlo. Además en ellas aparecía una velocidad constante (![]() ) que era independiente del observador o de la velocidad de la fuente.
) que era independiente del observador o de la velocidad de la fuente.
El hecho de que las ecuaciones de Maxwell no fuesen invariantes de Galileo se podía deber a tres motivos, principalmente:
- Las ecuaciones de Maxwell no son válidas
- Existe un sistema de referencia preferido (éter) respecto al cual se puede medir absolutamente cualquier movimiento
- Las transformaciones de Galileo no son las adecuadas
La primera de estas opciones se descartó casi de inmediato, las ecuaciones de Maxwell estaban harto comprobadas.
La segunda opción (que venía implicada por la tercera) no era muy creíble, ya que el éter debería presentar unas características totalmente contradictorias entre si.
Fue el experimento de Michelson-Morley, en 1887, el que proporcionó pruebas experimentales de la constancia de la velocidad de la luz, que se convirtió en uno de los postulados de la teoría de la relatividad. Esto implicaba que las transformaciones de Galileo no eran correctas.
1.2 El experimento de Michelson-Morley
El experimento de Michelson-Morley consistía en un interferómetro que mediante un mecanismo creaba un patrón de interferencias debido al desfase de la luz causado por la velocidad de la Tierra.
Se lanzaba un rayo de luz de una longitud de onda conocida (con una lámpara de sodio) que incidía en un espejo semiplateado. Este espejo tiene la propiedad de que refleja la mitad del rayo y la otra mitad la reflicte. Ahora tenemos dos rayos de igual longitud de onda que salen formando un ángulo recto entre ellos y van a dar a dos espejos donde se reflejan. Vuelven a incidir en el espejo semiplateado y vuelve a reflejarse una mitad de cada rayo y a reflectirse la otra. Sin preocuparnos de lo que le ocurre a los rayos que no nos interesan tomamos dos que vayan en la misma dirección.
Si existe alguna diferencia entre las longitudes de los brazos del interferómetro aparecerá un patrón de interferencias, o si esta distancia es igual pero los rayos se mueven a velocidades diferentes. Como los rayos que salen del espejo semiplateado forman un ángulo recto entre ellos uno se moverá en la misma dirección que la Tierra y otra en una dirección perpendicular (en el mejor de los casos, el interferómetro se podía rotar, de modo que cualquier combinación entre la dirección de un rayo y la dirección de movimiento de la Tierra era posible).
Al mover la posición del interferómetro (estaba situado sobre mercurio para poder girarlo) las rayas de interferencia se moverían (porque las velocidades también variarían) y observando cuánto se movieron podríamos comprobar la existencia del éter y la validez de las transformaciones de Galileo. Este interferómetro podía detectar una diferencia del 5%.
A partir del esquema del interferómetro podemos calcular el desfase entre un patrón de interferencias y otro. Calculemos primero el tiempo que le llevaría llegar de ![]() a
a ![]() y de
y de ![]() a
a ![]() : sea
: sea ![]() la velocidad de la luz y
la velocidad de la luz y ![]() la velocidad de la Tierra respecto al éter, entonces
la velocidad de la Tierra respecto al éter, entonces
Y el tiempo que tarda en ir de ![]() a
a ![]() es
es
Siendo el tiempo que tarda en ir de ![]() a
a ![]() el mismo (llamamos
el mismo (llamamos ![]() a la suma de estos dos últimos). Por tanto, si
a la suma de estos dos últimos). Por tanto, si ![]() podemos hacer una aproximación en serie de Taylor para los dos tiempos que tenemos y calcular la diferencia entre ellos:
podemos hacer una aproximación en serie de Taylor para los dos tiempos que tenemos y calcular la diferencia entre ellos:
En donde definimos
![]() .
.
Se puede ver que si giramos el interferómetro noventa grados entonces obtenemos
![]() . Esta diferencia en el camino, dividida entre el periodo de la onda, nos da el porcentaje que se desvía el patrón de interferencias:
. Esta diferencia en el camino, dividida entre el periodo de la onda, nos da el porcentaje que se desvía el patrón de interferencias:
En el interferómetro usado por Michelson y Morley los datos eran ![]() ,
,
![]() ,
,
![]() y
y
![]() , con lo que nos da un valor
, con lo que nos da un valor
![]() , que es un 37%.
, que es un 37%.
El valor medido experimentalmente fue cero, las transformaciones de Galileo no valen.
2 Postulados de la Relatividad
Dos son los postulados a partir de los cuales se desarrolla la teoría de la relatividad, la teoría que nos describe con exactitud los fenómenos que ocurren a altas velocidades:
- Las leyes que rigen los fenómenos físicos son idénticas en todos los sistemas de referencia inerciales.
- La velocidad de la luz en el vacío (que se denota como
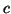 ) es una constante universal, independiente de todo movimiento relativo entre la fuente y el observador.
) es una constante universal, independiente de todo movimiento relativo entre la fuente y el observador.
Hay que hacer notar que el primero de estos dos postulados implica que sólo se pueden medir movimientos relativos de los sistemas inerciales, la idea de movimiento respecto a algo que esté quieto no tiene sentido. El segundo postulado nos dice que la velodicad de la luz en el vacío es una constante, pero no que es la velocidad máxima a la que se puede transmitir la información, este es un resultado que se deduce más adelante.
Tenemos, pues, estos dos sencillos postulados, veamos lo que implican, durante estos apuntes se notará como ![]() el sistema que se considera en reposo y como
el sistema que se considera en reposo y como ![]() el sistema en movimiento constante respecto a
el sistema en movimiento constante respecto a ![]() , de igual modo, todas las variables primadas estarán asociadas al sistema
, de igual modo, todas las variables primadas estarán asociadas al sistema ![]() mientras que las variables sin primar están asociadas al sistema
mientras que las variables sin primar están asociadas al sistema ![]() .
.
3 Transformaciones de Lorentz
3.1 Hipótesis lineal
Supongamos los sistemas de referencia ![]() y
y ![]() (moviéndose a una velocidad
(moviéndose a una velocidad ![]() con respecto a
con respecto a ![]() ) cuyos orígenes de coordenadas coinciden en el instante inicial (i.e.,
) cuyos orígenes de coordenadas coinciden en el instante inicial (i.e., ![]() ). Supongamos que el movimiento es a lo largo de la coordenada
). Supongamos que el movimiento es a lo largo de la coordenada ![]() . Según las transformaciones de Galileo sabíamos que
. Según las transformaciones de Galileo sabíamos que
![]() ,
,
![]() ,
,
![]() y
y ![]() . Sin embargo estamos intentando encontrar unas transformaciones diferentes a estas, pero que se reduzcan a ellas en algún caso especial. Para ello hacemos la siguiente hipótesis lineal:
. Sin embargo estamos intentando encontrar unas transformaciones diferentes a estas, pero que se reduzcan a ellas en algún caso especial. Para ello hacemos la siguiente hipótesis lineal:
La posición del origen de coordenadas ![]() en cada uno de los dos sistemas viene dado por
en cada uno de los dos sistemas viene dado por ![]() y
y ![]() ya que en el instante inicial ambos orígenes coincidían. Por tanto tenemos que
ya que en el instante inicial ambos orígenes coincidían. Por tanto tenemos que
Por tanto vemos que es necesario hallar el valor del factor adimensional ![]() .
.
3.2 Valor de gamma
Si en el origen de tiempos el origen de coordenadas de los sistemas ![]() y
y ![]() coinciden y se emite un rayo de luz en una dirección, según el segundo postulado de la relatividad, el frente de ondas de este rayo estará definido en ambos sistemas por1
coinciden y se emite un rayo de luz en una dirección, según el segundo postulado de la relatividad, el frente de ondas de este rayo estará definido en ambos sistemas por1
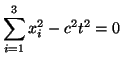 |
|||
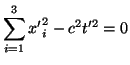 |
(9) |
Podemos suponer que
![]() y
y
![]() debido a que en esta teoría sólo tratamos con movimientos rectilíneos uniformes, así que tenemos que
debido a que en esta teoría sólo tratamos con movimientos rectilíneos uniformes, así que tenemos que
| (10) |
Es habitual definir
![]() .
.
Vemos que ![]() es un factor de proporcionalidad que toma un valor dependiendo de la velocidad
es un factor de proporcionalidad que toma un valor dependiendo de la velocidad ![]() con la que se mueve un sistema de referencia respecto al otro. Si este valor es
con la que se mueve un sistema de referencia respecto al otro. Si este valor es ![]() (el valor en el que los dos sistemas coincides, i.e. no hay movimiento relativo de uno con respecto al otro)
(el valor en el que los dos sistemas coincides, i.e. no hay movimiento relativo de uno con respecto al otro) ![]() , como debe ser, ya que los dos sistemas son el mismo y por tanto las coordenadas también han de coincidir. Si el valor es
, como debe ser, ya que los dos sistemas son el mismo y por tanto las coordenadas también han de coincidir. Si el valor es ![]() se puede comprobar fácilmente que
se puede comprobar fácilmente que
![]() . Para valores
. Para valores ![]() obtenemos en el denominador una raíz de un número negativa, por lo que
obtenemos en el denominador una raíz de un número negativa, por lo que ![]() deja de estar definida.
deja de estar definida.
Por tanto vemos que ![]() toma siempre un valor dentro del intervalo
toma siempre un valor dentro del intervalo
![]() , con
, con ![]() perteneciente al intervalo
perteneciente al intervalo ![]() (como
(como ![]() va al cuadrado
va al cuadrado ![]() sólo depende de su módulo, no de su dirección).
sólo depende de su módulo, no de su dirección).
El coeficiente ![]() es la fracción de la velocidad de la luz. Si
es la fracción de la velocidad de la luz. Si ![]() entonces
entonces ![]() , mientras que si
, mientras que si ![]() entonces
entonces
![]() .
.
3.3 Transformaciones de coordenadas
Conocido ya el valor de ![]() tenemos que nuestra hipótesis lineal toma la forma siguiente
tenemos que nuestra hipótesis lineal toma la forma siguiente
Y a partir de ahí podemos despejar las transformaciones para el tiempo
| (14) |
Ya que
![]() . Se puede demostrar de modo análogo que
. Se puede demostrar de modo análogo que
4 Implicaciones de las transformaciones de Lorentz
4.1 Relatividad de la simultaneidad, causalidad
Una de las implicaciones más importantes que acarrean las transformaciones de Lorentz es la de que si dos sucesos son simultáneos en el sistema
Además se puede ver que ![]() es la máxima velocidad para una señal, ya que en este valor el factor
es la máxima velocidad para una señal, ya que en este valor el factor ![]() se hace infinito y esto implicaría una diferencia temporal infinita; además también se observa que la causa siempre ha de ser anterior al efecto que produce en cualquier sistema.
se hace infinito y esto implicaría una diferencia temporal infinita; además también se observa que la causa siempre ha de ser anterior al efecto que produce en cualquier sistema.
4.2 Relatividad de la colocalidad (dilatación temporal)
Imaginemos dos sucesos que son colocales en el sistema ![]() (
(
![]() ), en S
), en S
4.3 Dilatación temporal
Supongamos que tenemos una medida temporal
![]() en el sistema
en el sistema ![]() y queremos calcular
y queremos calcular
![]() en el sistema
en el sistema ![]() . Según las transformaciones de Lorentz tenemos que
. Según las transformaciones de Lorentz tenemos que
Pero estas medidas temporales se hacen en la misma localización, de modo que
![]() , así que obtenemos
, así que obtenemos
Fenómeno conocido como la dilatación temporal. Hay que hacer notar que según este resultado el tiempo medido en el sistema en reposo es siempre menor que el tiempo medido en cualquier otro sistema de referencia inercial.
4.4 Contracción de Lorentz
Supongamos ahora que tenemos una medida de la longitud
![]() en el sismema
en el sismema ![]() y queremos calcular cuanto valdría
y queremos calcular cuanto valdría
![]() usando las transformaciones de Lorentz.
usando las transformaciones de Lorentz.
Pero la medida de la longitud se hicen midiendo ![]() y
y ![]() a la vez, de modo que
a la vez, de modo que
![]() , por lo tanto:
, por lo tanto:
Fenómeno conocido como la contracción de longitudes o contracción de Lorentz. Esta ecuación implica que la longitud ![]() medida en el sistema en reposo es siempre mayor que la longitud
medida en el sistema en reposo es siempre mayor que la longitud ![]() medida en un sistema de referencia inercial en movimiento.
medida en un sistema de referencia inercial en movimiento.
4.5 Adición de velocidades
La velocidad es la derivada temporal de la posición, pero hemos de tener en cuenta que el tiempo no es universal, sino relativo, de modo que al hablar de la velocidad en relatividad tenemos que saber si nos referimos al sistema en reposo al que se mueve con movimiento rectilíneo uniforme:
Para calcular estas velocidades, por lo tanto, hemos de saber qué forma tienen los diferenciales de posición y de tiempo. Estas formas salen fácilmente a partir de las transformaciones de Lorentz [(12), (15) y (16))
Y por tanto obtenemos
Y esa es la fórmula de adición de velocidades en relatividad especial. Hay que hacer notar que en el caso de que
![]() (es decir, c es muy alto en comparación con las otras velocidades) esta relación de velocidades se reduce a la relación galineana que se emplea en mecánica clásica (es decir
(es decir, c es muy alto en comparación con las otras velocidades) esta relación de velocidades se reduce a la relación galineana que se emplea en mecánica clásica (es decir ![]() ).
).
También se puede observar quw si tanto ![]() y
y ![]() obtenemos
obtenemos
| (26) |
O que si ![]() y
y ![]()
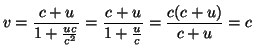 |
(27) |
Resultados consistentes con el hecho de que no se puede superar la velocidad de la luz en el vacío en ningún sistema de referencia.
5 Cuadrivectores
Un cuadrivector es una magnitud que consta de cuatro componentes y que se transforma de acuerdo con2
| (28) |
en donde
![]() son los componentes del tensor de Lorentz:
son los componentes del tensor de Lorentz:
Definimos el modulo de un cuadrivector como
| (30) |
donde
![]() son los componentes de la métrica de Minkowski:
son los componentes de la métrica de Minkowski:
Por lo que
| (32) |
El módulo de un cuadrivector es siempre un escalar (con lo cual es un invariante)
5.1 Cuadrivector posición
Definimos el cuadrivector posición como
![]() (vemos que
(vemos que ![]() , notación que se emplea para los sumatorios).
, notación que se emplea para los sumatorios).
Si queremos transformar las coordenadas de este cuadrivector obtenemos (empleando el tensor de Lorentz (29))
que al resolverlo nos da justamente las transformaciones de Lorentz, como se comprueba fácilmente.
5.1.1 Intervalo
Ahora imaginemos que tenemos dos sucesos
![]() y
y
![]() , el intervalo se define como el módulo de la diferencia de estos dos sucesos, es decir:
, el intervalo se define como el módulo de la diferencia de estos dos sucesos, es decir:
Que, al ser el módulo de un cuadrivector, es un escalar y por tanto invariante. Hay que notar que
![]() no es definido positivo. Si el intervalo es igual a cero se dice que es un intervalo tipo-luz (light-like). Si el intervalo es negativo se dice que es un intervalo temporal (time-like), ya que en este tipo de intervalo los dos sucesos pueden estar relacionados causalmente (suceder en el mismo punto a tiempos distintos). Por último, si el intervalo es positivo se llama intervalo tipo espacio (space-like), y pueden ser dos sucesos simultáneos que ocurren en tiempos distintos.
no es definido positivo. Si el intervalo es igual a cero se dice que es un intervalo tipo-luz (light-like). Si el intervalo es negativo se dice que es un intervalo temporal (time-like), ya que en este tipo de intervalo los dos sucesos pueden estar relacionados causalmente (suceder en el mismo punto a tiempos distintos). Por último, si el intervalo es positivo se llama intervalo tipo espacio (space-like), y pueden ser dos sucesos simultáneos que ocurren en tiempos distintos.
Se puede definir el intervalo infinitesimal como
En donde
![]() y análogamente para
y análogamente para ![]() ,
, ![]() y
y ![]() .
.
5.1.2 Tiempo propio
Definimos el tiempo propio como
![]() , de modo que tenemos que
, de modo que tenemos que
Por lo que ![]() es el tiempo más pequeño, es decir, el tiempo medido en el sistema solidario con el suceso.
es el tiempo más pequeño, es decir, el tiempo medido en el sistema solidario con el suceso.
5.2 Cuadrivector velocidad
Podemos definir la velocidad como la variación temporal de la posición. Así que podemos definir el cuadrivector velocidad como
En donde empleamos el diferencial ![]() porque es el único invariante temporal que tenemos, hay que fijarse que
porque es el único invariante temporal que tenemos, hay que fijarse que ![]() es un diferencial de un componente de
es un diferencial de un componente de
![]() .
.
Podemos hallar el módulo del cuadrivector velocidad de un modo simple, resultando
![]() .
.
5.3 Cuadrivector momento
Para obtener el cuadrivector momento (cuadrimomento) debemos multiplicar la cuadrivelocidad por un escalar con dimensiones de masa, al que llamaremos ![]() , por tanto tenemos que
, por tanto tenemos que
![]() .
.
5.3.1 Masa relativista
Si hacemos la analogía con el momento de la mecánica clásica
![]() obtenemos la relación entre la masa de un objeto y el escalar
obtenemos la relación entre la masa de un objeto y el escalar ![]() de modo que
de modo que
![]() . A partir de ahora llamaremos masa relativista (inercial) a
. A partir de ahora llamaremos masa relativista (inercial) a ![]() y masa en reposo a
y masa en reposo a ![]() .
.
6 Dinámica relativista
6.1 Fuerza
Newton definió la fuerza como la derivada temporal del momento lineal en sus Principia Mathematica, podríamos definir el cuadrivector fuerza como
![]() , pero esta magnitud no se emplea en relatividad, por lo que no se profundiza más en ella.
, pero esta magnitud no se emplea en relatividad, por lo que no se profundiza más en ella.
De todos modos tenemos que
![]()
6.2 Energía
Por un lado tenemos el resultado conocido
![]() donde T es la energía cinética. Por otro lado tenemos
donde T es la energía cinética. Por otro lado tenemos
La última igualdad de (38) se deduce fácilmente del cálculo del módulo de la cuadrivelocidad. Tenemos por tanto una igualdad
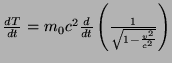 , que integrándola entre el reposo y un tiempo cualquiera t nos da
, que integrándola entre el reposo y un tiempo cualquiera t nos da
Ya que ![]() por partir del reposo. Vemos por tanto que
por partir del reposo. Vemos por tanto que
![]() , en donde
, en donde ![]() es la energía cinética y
es la energía cinética y
![]() es la energía en reposo que toda masa posee sólo por tener masa. De este modo tenemos que la energía total es
es la energía en reposo que toda masa posee sólo por tener masa. De este modo tenemos que la energía total es
![]() .
.
Si hacemos una aproximación de la energía cinética para velocidades pequeñas obtenemos el resultado conocido de
![]() .
.
Observamos que si dividimos la energía total por la velocidad de la luz obtenemos el primer componente del cuadrimomento, por lo que podemos escribir
![]() . Su módulo según esta expresión es
. Su módulo según esta expresión es
Que para una partícula sin masa (como el fotón) se reduce a la expresión ![]() , con una indeterminación del tipo
, con una indeterminación del tipo
![]() en el cálculo de
en el cálculo de ![]() .
.
A. Las transformaciones de Lorentz como rotación imaginaria
Veíamos en (33) que la transformación de Lorentz del cuadrivector posición se calcula mediante
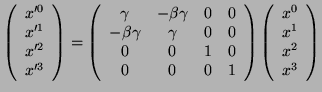 |
(41) |
Que podemos reducir a
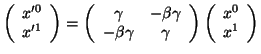 |
(42) |
Expresión que recuerda a la de una rotación. En efecto, vemos que resolviendo el determinante de la ``matriz de giro'' tenemos
![]() . Llamemos entonces
. Llamemos entonces
![]() y
y
![]() :
:
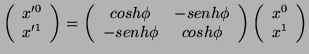 |
(43) |
Por tanto
![]() . Si denotamos
. Si denotamos
![]() tenemos que
tenemos que
![]() y
y
![]() , por tanto
, por tanto
![]() , que es lo mismo que
, que es lo mismo que
![]() , con lo que nos queda la expresión
, con lo que nos queda la expresión
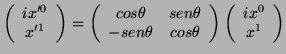 |
(44) |
Que es la expresión de una rotación. Esto demuestra que las rotaciones de Lorentz son ``rotaciones complejas'' en el espacio de cuatro dimensiones. Este hecho fue descubierto por Minkowski y demuestra que el espacio y el tiempo están mucho más ligados de lo que parece a la vista de las transformaciones de Lorentz.
B. Comentario a la óptica relativista
Como vimos en la ecuación (22) un cuerpo se ve acortado desde un sistema de referencia respecto al que se esté moviendo, y este acortamiento (en la dirección del movimiento) será mayor o menor dependiendo de la velocidad relativa entre los dos sistemas. Por tanto un cubo de lado ![]() será un prisma, supongamos que se mueve en la dirección de una de sus caras, entonces el cubo será un prisma de altura
será un prisma, supongamos que se mueve en la dirección de una de sus caras, entonces el cubo será un prisma de altura ![]() pero de longitud
pero de longitud
![]() .
.
Sin embargo lo que un observador vería no sería un prisma de esas características, sino un cubo girado un cierto ángulo que depende de la velocidad relativa entre ambos sistemas. Este hecho se debe a que para que la luz procedente de los diferentes vértices alcance al obserador en el mismo instante, la luz procedente de cada vértice debe atravesar una distancia diferente y por tanto se encontrará, en realidad, en otra posición.
Igualmente una esfera móvil no se vería con forma elíptica, sino que se vería como una esfera de igual radio (girada un cierto ángulo, pero como es una esfera esto no se aprecia).3
C. Línea de universo, diagramas de Minkowski
La historia de una partícula en movimiento describe una línea en el espacio de Minkowski. Cuando se considera sólo una dimensión el espacio de Minkowski se representa como en la figura 4. En el caso de dos dimensiones espaciales se representaría mediante un cono (llamado cono de luz) y en el caso de representar las tres dimensiones un hipercono.
Cuando se unen dos sucesos con un intervalo tipo luz entre ellos la historia de la partícula transcurre por la frontera entre la región rallada y la región sin rallar. Si los sucesos están unidos con un intervalo tipo tiempo la línea de historia está dentro del cono de luz (la región rallada). Si los sucesos están unidos con un intervalo tipo espacio están fuera del cono de luz.
Hay que remarcar que la línea de historia de una partícula está siempre dentro del cono de luz, ya que es la región en la que los sucesos pueden estar relacionados causalmente. Por la misma razón, ninguna línea de historia puede atravesar el cono de luz. La línea de coordenada espacial es el presente, siendo el origen del cono de luz la posición de la partícula. Normalmente al cono superior se le llama cono futuro (porque están en un tiempo posterior al presente de la partícula) y al cono inferior se le llama cono pasado. Al resto de las regiones se las suele llamar meta-presente.
Las transformaciones de Lorentz lo que hacen es estrechar el cono de luz, de modo que los ejes ![]() y
y ![]() se van acercando a la línea de luz. Este estrechamiento del cono depende de la velocidad relativa entre los dos sistemas de referencia y en el caso de que la velocidad sea
se van acercando a la línea de luz. Este estrechamiento del cono depende de la velocidad relativa entre los dos sistemas de referencia y en el caso de que la velocidad sea ![]() el cono colapsa en una línea (véase (25)).
el cono colapsa en una línea (véase (25)).
Notas al pie
- ... por1
- Nótese que aquí hay ya una diferencia con la visión clásica: mientras en esta el tiempo sería igual en ambas y la velocidad de la luz dependería del sistema, en la teoría de la relatividad
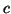 es la misma y es el tiempo el que varía en ambos sistemas
es la misma y es el tiempo el que varía en ambos sistemas
- ... con2
- En relatividad es normal denotar con letras griegas los índices que van desde 0 a 3 (o en alguna literatura de 1 a 4) y con letras latinas los que van de 1 a 3; también se emplean índices covariantes (subíndices) y contravariantes(superíndices, no confundir con exponentes), pero no se explicará la distinción aquí.
- ... aprecia).3
- Véase Dinámica clásica de las Partículas y Sistemas, Jerry B. Marion, Ed. Reverté


![\includegraphics[width=0.5\textwidth]{michelson}](img2.png)
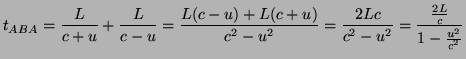
![\includegraphics[width=0.4\textwidth]{michelson2}](img8.png)
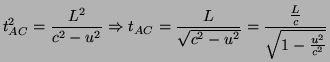
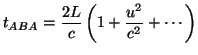
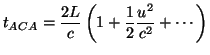
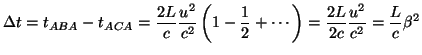
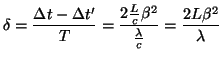
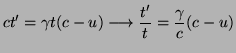
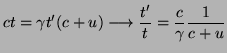
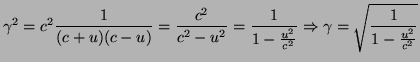
![\includegraphics[width=0.6\textwidth]{gamma}](img56.png)
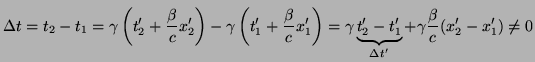
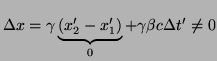
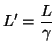
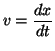
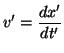
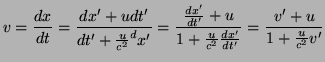
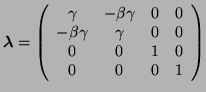
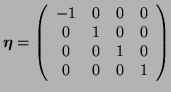
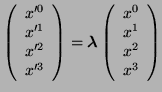
![$\displaystyle d\tau=\sqrt{dt^{2}-\frac{1}{c^{2}}(dx^{2}+dy^{2}+dz^{2})}=dt\sqrt...
...ht)^{2}+ \left(\frac{dy}{dt}\right)^{2}+ \left(\frac{dz}{dt}\right)^{2}\right]}$](img117.png)
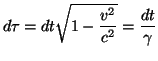
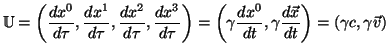
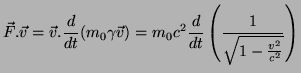
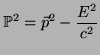
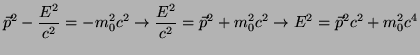
![\includegraphics[width=0.5\textwidth]{minkowski}](img166.png)
