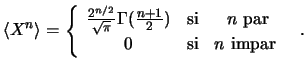Introducción a la teoría de probabilidad
pod
Date: Abril - mayo de 2001
Introducción
Este documento presenta brevemente los principios de la teoría de la probabilidad. Dicha teoría representa una de las herramientas matemáticas más importantes para la física, en especial para la teoría de la Mecánica Cuántica, así como en los desarrollos de la Física Estadística. La teoría de la probabilidad se presenta en forma de apuntes esquemáticos y sin demostraciones.
3.1. Interpretación de la probabilidad
- Probabilidad clásica (a priori):
- Asigna una probabilidad a un suceso antes de que este ocurra, basándose en el principio de simetría (casos favorables entre casos totales).
- Probabilidad frecuencial:
- La probabilidad de un suceso es la frecuencia con la que se observa.
- Probabilidad subjetiva:
- Se asigna la probabilidad a partir de la información previa.
- Probabilidad como lógica:
- Basada en razonamientos lógicos.
- Probabilidad geométrica:
- Basada en una medida de los sucesos (medida de los sucesos favorables entre medida total).
3.2. Probabilidad axiomática
La definición axiomática de la probabilidad es:
se le llama medida de la probabilidad si cumple las siguientes condiciones:
- Si
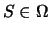 , entonces existe un valor
, entonces existe un valor
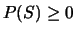 , al que llamaremos probabilidad de S.
, al que llamaremos probabilidad de S.
- La probabilidad del suceso seguro (espacio muestral) es
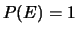 .
.
- Dada una sucesión numerable de sucesos disjuntos (mutuamente excluyentes dos a dos)
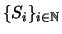 ,
entonces:
,
entonces:
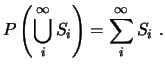
A partir de estos axiomas, se pueden demostrar las siguientes propiedades de la probabilidad.
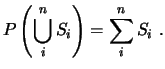
En general, para una colección finita de sucesos
![]() , se tiene:
, se tiene:
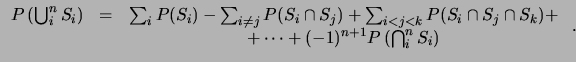
3.3. Probabilidad condicionada
La probabilidad de que se verifique un suceso
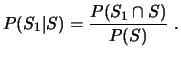
Las principales propiedades de la probabilidad condicionada son:
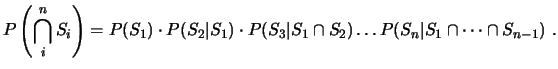
- Mutuamente disjuntos,
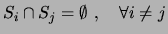
- Recubren el espacio muestral
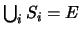
- Tienen partes comunes con
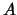 ,
,
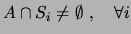
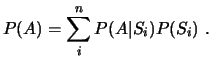
El teorema de la probabilidad total proporciona una manera de calcular la contribución de cada una de las causas (![]() )
a la probabilidad de la consecuencia (
)
a la probabilidad de la consecuencia (![]() ).
).
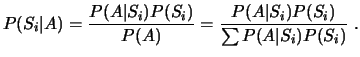
Donde
![]() es la probabilidad a posteriori o hipótesis; y
es la probabilidad a posteriori o hipótesis; y
![]() es la verosimilitud.
es la verosimilitud.
3.4. Independencia de sucesos
Esta definición no es suficiente si tenemos un mayor número de sucesos.
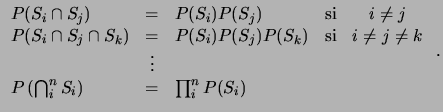
3.5. Variable aleatoria o estocástica discreta
Estudiaremos una variable aleatoria
La función de distribución de probabilidad discreta debe verificar:
- Cota:
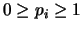
- Normalización
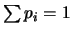
Algunas definiciones de utilidad:
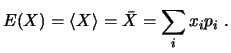
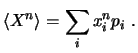
La desviación típica se define como la raíz cuadrada de la varianza:
Algunas propiedades del operador valor esperado vienen dados por el siguiente
- Escala:
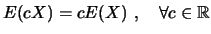
- Adición:
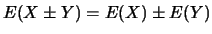
- Independencia:
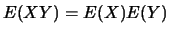 si
si 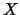 e
e 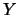 son independientes.
son independientes.
- Composición:
![$ E[ g(x) ] = \sum g(x_i) p_i$](img53.png)
- No desviado:
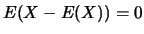
Por último, veamos algunas propiedades de la varianza:
- Origen:
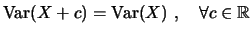
- Adición:
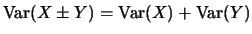 si
si  e
e  son independientes.
son independientes.
- Escala:
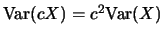
3.6. Variables aleatorias continuas
Para una variable aleatoria que puede tomar cualquier valor dentro de un rango (que puede ser infinito), se definen las funciones de densidad de probabilidad y ´de distribución acumulada.
La función de densidad de probabilidad ![]() debe cumplir:
debe cumplir:
- No negatividad:
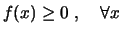
- Normalización:
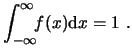
- Probabilidad:
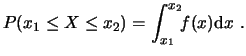
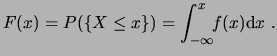
La función de distribución acumulada debe cumplir:
- Límite inferior:
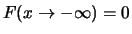
- Límite superior:
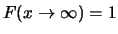
- Monotonía:
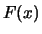 es creciente.
es creciente.
- Probabilidad de un rango:
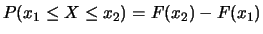
Igual que para las distribuciones discretas, podemos definir los momentos de una distribución:
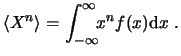
El valor esperado se define como el momento de orden ![]() .
.
La varianza y la desviación tienen la misma definición que en el caso discreto.
Otra definición de interés resulta la función característica de la distribución:
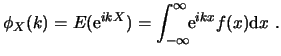
El desarrollo de Taylor de la exponencial muestra que los momentos de cada orden son los coeficientes de la expansión:
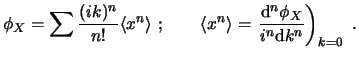
Por la definición de valor esperado, podemos ver que la función característica es la transformada de Fourier de la función de densidad de probabilidad, por tanto, esta última se puede calcular de la primera mediante:
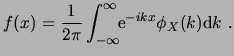
3.7. Ejemplos de distribuciones
3.7.1. Distribuciones discretas
3.7.1.1. Pruebas de Bernoulli
Experimento con dos resultados posibles (1 y 0, con probabilidades respectivas
3.7.1.2. Distribución binomial
Una variable discreta
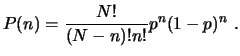
La distribución normal tiene por valor esperado ![]() , su momento de orden 2 es
, su momento de orden 2 es
![]() y su varianza es
y su varianza es
![]()
3.7.1.3. Distribución geométrica
La distribución geométrica representa la probabilidad de que, en una serie de pruebas de Bernoulli, el primer éxito (1) se obtenga en la n-ésima tirada. La función de distribución es:
Su valor esperado es
![]() y su desviación típica
y su desviación típica
![]()
3.7.1.4. Distribución de Poisson
Una variable aleatoria discreta
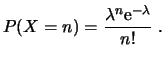
donde
3.7.2. Distribuciones continuas. Distribución Gaussiana y normal
La versión discreta de la distribución normal es:
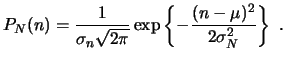
La variante continua de la distribución Gaussiana, con parámetros ![]() y
y ![]() (valor esperado y desviación típica),
viene definida por la función de densidad Gaussiana:
(valor esperado y desviación típica),
viene definida por la función de densidad Gaussiana:
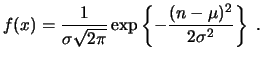
Por cambios de variables, se puede reducir a la distribución normal, un caso especial donde ![]() y
y
![]() .
Los momentos de la distribución normal vienen dados por:
.
Los momentos de la distribución normal vienen dados por: