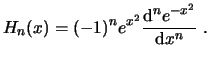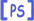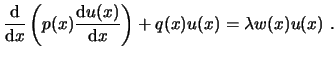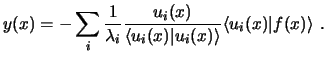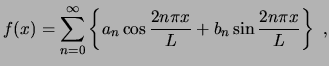Bájatelo (formato ps) Formato post-script

Teoría de Strum-Liouville:
funciones propias y ortogonales

pod


Date: Febrero - marzo de 2001

Introducción

Este documento presenta brevemente los principios de la teoría de Strum-Liouville sobre las ecuaciones diferenciales. Dicha teoría representa una de las herramientas matemáticas más importantes para la física, tanto para temas clásicos (propagación de ondas, procesos de dispersión, etc.) como para modernos (ecuaciones de Schödinger y Dirac, etc.). Además, se tratan alguna de las funciones especiales más importantes en la física, describiendo sus propiedades a partir de la teoría de Strum-Liouville. Este documento se presenta en forma de apuntes esquemáticos y sin demostraciones.

1 Problema de valores propios.

Dado un operador diferencial de segundo orden, $ \ensuremath{\mathcal{L}}\equiv p_0(x)\frac{\ensuremath{\mathrm{d}}^2 \_}{\ensu... ... p_1(x) \frac{\ensuremath{\mathrm{d}}\_}{\ensuremath{\mathrm{d}}x} + p_2(x) \_ $ , se define su operador adjunto de la siguiente manera:

$\displaystyle \overline{\ensuremath{\mathcal{L}}} \equiv \frac{\ensuremath{\mat... ...\ensuremath{\mathrm{d}}}{\ensuremath{\mathrm{d}}x} [p_1(x) \_] + p_2(x) \_ . $

En el caso que $ \ensuremath{\mathcal{L}}= \overline{\ensuremath{\mathcal{L}}}$ , se dice que el operador $ \mathcal{L}$ es autoadjunto. Para que esto pase, se ha de cumplir que $ p_0'(x) = p_1(x)$ . Si esta condición no se cumple, se puede definir un operador $ \mathbf{L}$ asociado a $ \mathcal{L}$ que cumpla la condición:

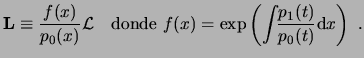
$\displaystyle \mathbf{L} \equiv \frac{f(x)}{p_0(x)} \ensuremath{\mathcal{L}}\qu... ... \exp\left( \int\!\!\frac{p_1(t)}{p_0(t)} \ensuremath{\mathrm{d}}x \right) . $

Una ecuación diferencial del tipo $ \ensuremath{\mathcal{L}}u(x) = \lambda u(x)$ define un problema de valores propios, y puede escribirse de la siguiente manera:

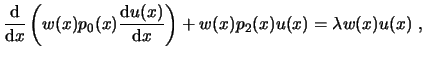
$\displaystyle \frac{\ensuremath{\mathrm{d}}}{\ensuremath{\mathrm{d}}x} \left( w... ...}{\ensuremath{\mathrm{d}}x} \right) + w(x) p_2(x) u(x) = \lambda w(x) u(x) , $

Donde

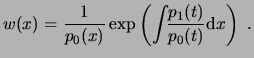
$\displaystyle w(x) = \frac{1}{p_0(x)} \exp\left( \int\!\!\frac{p_1(t)}{p_0(t)} \ensuremath{\mathrm{d}}x \right) . $

Por simplicidad, definimos $ p(x) \equiv w(x) p_0(x)$ y $ q(x) \equiv w(x) p_2(x)$ . La ecuación resultante se escribe como

$\displaystyle \frac{\ensuremath{\mathrm{d}}}{\ensuremath{\mathrm{d}}x} \left( p... ...{d}}u(x)}{\ensuremath{\mathrm{d}}x} \right) + q(x) u(x) = \lambda w(x) u(x) .$ (1)

Los valores de $ \lambda$ que cumplen la ecuación y las condiciones de contorno del problema se llaman valores propios. y las soluciones $ u_{\lambda}(x)$ para un valor de $ \lambda$ fijo se denominan funciones propias. Las condiciones de contorno indican los posibles valores de $ \lambda$ . Dichas condiciones se pueden presentar de diversas maneras. Las más usuales son:

Condiciones de Cauchy:
Se especifica la función y sus derivadas normales en los límites del intervalo.
Condiciones de Diriched:
Se da el valor de la función en los límites del intervalo.
Condiciones de Newman:
Se da el valor de las derivadas normales en los límites del intervalo.

Dichas condiciones de contorno pueden expresarse de alguna de las formas siguientes:

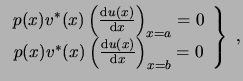
$\displaystyle \left.\begin{array}{c} p(x)v^*(x) \left( \frac{\ensuremath{\mathr... ...m{d}}u(x)}{\ensuremath{\mathrm{d}}x} \right)_{x=b} = 0 \end{array}\right\} , $

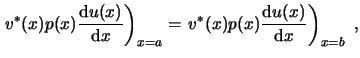
$\displaystyle \left. v^*(x) p(x) \frac{\ensuremath{\mathrm{d}}u(x)}{\ensuremath... ... \frac{\ensuremath{\mathrm{d}}u(x)}{\ensuremath{\mathrm{d}}x} \right)_{x=b} ,$

$\displaystyle \left.\begin{array}{c} p(a) \left[ \alpha_1 u(a) + \beta_1 \left.... ...)}{\ensuremath{\mathrm{d}}x} \right)_{x=b} \right] = 0 \end{array}\right\} . $

Un operador autoadjunto $ \mathcal{L}$ cuyas soluciones $ u(x)$ y $ v(x)$ cumplen las condiciones de contorno

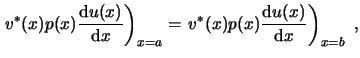
$\displaystyle \left. v^*(x) p(x) \frac{\ensuremath{\mathrm{d}}u(x)}{\ensuremath... ... \frac{\ensuremath{\mathrm{d}}u(x)}{\ensuremath{\mathrm{d}}x} \right)_{x=b} ,$

se denomina operador Hermítico. La condición de Hermiticidad que $ \mathcal{L}$ debe cumplir, además de las condiciones de contorno, es:

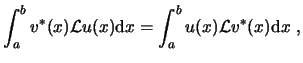
$\displaystyle \int_a^b v^*(x) \ensuremath{\mathcal{L}}u(x) \ensuremath{\mathrm{d}}x = \int_a^b u(x) \ensuremath{\mathcal{L}}v^*(x) \ensuremath{\mathrm{d}}x , $

Un operador hermítico cumple las siguientes propiedades:

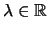
  1. Sus valores propios son reales, $ \lambda \in \mathbb{R}$
  2. Sus funciones propias son ortogonales.
  3. La solución general es una combinación lineal infinita de funciones propias.
  4. Las funciones propias son un conjunto completo.

Se define el producto escalar de dos funciones de la forma siguiente:

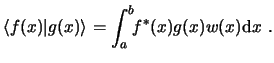
$\displaystyle \langle f(x) \vert g(x) \rangle = \int_a^b\!\!f^*(x) g(x) w(x) \ensuremath{\mathrm{d}}x . $

El producto escalar así definido cumple las propiedades de commutividad, no negatividad, linealidad y la desigualdad de Schwarz. La norma se define a partir de $ \Vert f(x) \Vert = \sqrt{\langle f(x) \vert f(x) \rangle}$ .

En el caso de que diversas funciones propias tengan valores propios iguales, no se puede asegurar la ortogonalidad de las funciones propias. Mediante el método de ortonormalización de Gram-Schmidt se puede obtener un segundo conjunto de funciones propias ortonormales. Según este método, la i-ésima función del nuevo conjunto viene dada por:

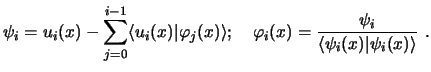
$\displaystyle \psi_i = u_i(x) - \sum_{j=0}^{i-1} \langle u_i(x) \vert \varphi_j... ...ad \varphi_i(x) = \frac{\psi_i}{\langle \psi_i(x) \vert \psi_i(x) \rangle} . $

Al ser las funciones propias un conjunto completo toda función continua por partes puede expresarse como combinación de las funciones propias, de forma que el error cuadrático media tiende a cero a medida que se añaden más funciones propias al desarrollo. El desarrollo se puede escribir de la forma siguiente:

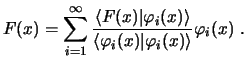
$\displaystyle F(x) = \sum_{i=1}^{\infty} \frac{\langle F(x) \vert \varphi_i(x) \rangle}{\langle \varphi_i(x) \vert \varphi_i(x) \rangle} \varphi_i(x) . $

Los coeficientes se denominan $ a_n = \frac{\langle F(x) \vert \varphi_i(x) \rangle} {\langle \varphi_i(x) \vert \varphi_i(x) \rangle}$ . Estos cumplen la desigualdad de Bessel $ \int_a^b F^2(x) w(x) \ensuremath{\mathrm{d}}x \ge \sum_{j=0}^N a^2_n$ . Un caso particular es la relación de Parseval $ \int_a^b F^2(x) w(x) \ensuremath{\mathrm{d}}x = \sum_{j=0}^{\infty} a^2_n$ .

En estas condiciones, la solución general de una ecuación del tipo

$\displaystyle \ensuremath{\mathcal{L}}y(x) = f(x) $

puede expresarse, desarrollando la solución de la forma $ y(x) = \sum a_n u_n(x)$ , en términos de las funciones propias de $ \mathcal{L}$ . Aplicando el método de superposición se obtiene la solución final:

$\displaystyle y(x) = -\sum_i \frac{1}{\lambda_i} \frac{u_i(x)}{\langle u_i(x) \vert u_i(x) \rangle} \langle u_i(x) \vert f(x) \rangle .$ (2)

Otro método para obtener la solución general de la ecuación inhomogénea es la función de Green, que es la solución de $ \ensuremath{\mathcal{L}}G(x,z) = \delta(x-z)$ , y que viene dada por $ G(x,z) = -\sum_i \lambda_i^{-1} u_i(x) u^*_i(z)$ . La solución general se expresa de la forma:

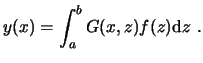
$\displaystyle y(x) = \int_a^b G(x,z) f(z) \ensuremath{\mathrm{d}}z . $

2 Series de Fourier

Toda función puede expresarse en función de combinaciones lineales de las funciones propias del problema de valores propios $ u''(x) + \lambda u(x) = 0$ , con las condiciones adecuadas entre 0 y $ L$ , las funciones propias son:

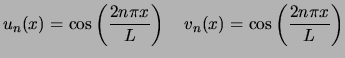
$\displaystyle u_n(x) = \cos\left(\frac{2n\pi x}{L}\right) \quad v_n(x) = \cos\left(\frac{2n\pi x}{L}\right) $

Por tanto, toda función continua por partes admite el desarrollo:

$\displaystyle f(x) = \sum_{n=0}^{\infty} \left\{ a_n \cos \frac{2n\pi x}{L} + b_n \sin \frac{2n\pi x}{L} \right\} ,$ (3)

donde

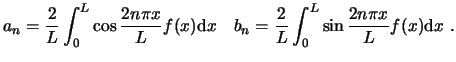
$\displaystyle a_n = \frac{2}{L} \int_0^L \cos \frac{2n\pi x}{L} f(x) \ensuremat... ...= \frac{2}{L} \int_0^L \sin\frac{2n\pi x}{L} f(x) \ensuremath{\mathrm{d}}x . $

De igual forma, se puede definir el desarrollo de Fourier en exponenciales complejas de la manera siguiente:

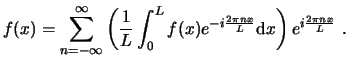
$\displaystyle f(x) = \sum_{n=-\infty}^{\infty} \left( \frac{1}{L} \int^L_0 f(x)... ...frac{2\pi n x}{L}}\ensuremath{\mathrm{d}}x \right) e^{i\frac{2\pi n x}{L}} . $

3 Funciones especiales

3.1 Función Gamma de Euler

La función gamma de Euler se define mediante la integral:

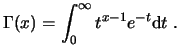
$\displaystyle \Gamma(x) = \int_0^{\infty} t^{x-1}e^{-t} \ensuremath{\mathrm{d}}t . $

Existe la ley de recurrencia $ \Gamma(x+1) = x \Gamma(x)$ . Por tanto, para $ n\in \mathbb{N}$ se tiene $ \Gamma(n+1) = n!$ . Esta ley sirve para extender la función Gamma a valores negativos no enteros. En concreto, se tiene

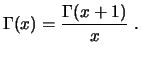
$\displaystyle \Gamma(x) = \frac{\Gamma(x+1)}{x} .$

La derivada de la función Gamma viene dada por

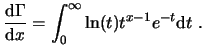
$\displaystyle \frac{\ensuremath{\mathrm{d}}\Gamma}{\ensuremath{\mathrm{d}}x} = \int_0^{\infty} \ln(t) t^{x-1} e^{-t} \ensuremath{\mathrm{d}}t . $

La constante de Euler viene dada por

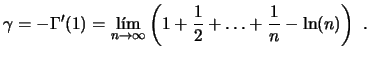
$\displaystyle \gamma = - \Gamma'(1) = \lim_{n \to \infty} \left( 1 + \frac{1}{2} + \ldots + \frac{1}{n} - \ln(n) \right) .$

Por último, la formula de reflexión viene dada por $ \Gamma(x)\Gamma(1-x) = \frac{\pi}{\sin(\pi x)}$ .

3.2 Funciones de Bessel

La ecuación de Bessel de orden $ \nu$ es

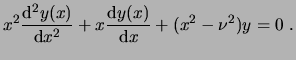
$\displaystyle x^2 \frac{\ensuremath{\mathrm{d}}^2y(x)}{\ensuremath{\mathrm{d}}x... ...{\ensuremath{\mathrm{d}}y(x)}{\ensuremath{\mathrm{d}}x} + (x^2 - \nu^2)y=0 . $

La función de Bessel de orden $ \nu$ se define por:

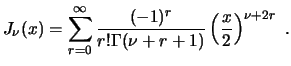
$\displaystyle J_{\nu}(x) = \sum_{r=0}^{\infty} \frac{(-1)^r}{r! \Gamma(\nu+r+1)} \left( \frac{x}{2} \right)^{\nu+2r} . $

La solución general de la función de Bessel para $ \nu \not\in \mathbb{N}$ es

$\displaystyle y(x) = A J_\nu (x) + B J_{-\nu} (x) \quad \textrm{para }\nu \not\in \mathbb{N} . $

Para $ \nu = n \in \mathbb{N}$ , la función de Bessel de orden $ n$ se puede escribir como

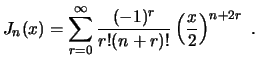
$\displaystyle J_n(x) = \sum_{r=0}^{\infty} \frac{(-1)^r}{r! (n+r)!} \left( \frac{x}{2} \right)^{n+2r} . $

Las funciones de Bessel para $ -n$ con $ n\in \mathbb{N}$ se puede escribir como $ J_{-n}(x) = (-1)^n J_n(x)$ . Por tanto hace falta otra solución para completar la expresión general. La función de Bessel $ Y_\nu(x)$ es la solución de la ecuación para $ \nu = -n$ , si $ n\in \mathbb{N}$ . Las funciones $ Y_n(x)$ siempre divergen para $ x \to 0$ . Se puede expresar como

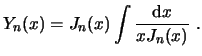
$\displaystyle Y_n(x) = J_n(x) \int \frac{\ensuremath{\mathrm{d}}x}{x J_n(x)} . $

Por tanto, la solución general para $ \nu = n \in \mathbb{N}$ es:

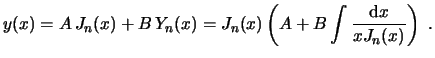
$\displaystyle y(x)= A J_n(x) + B Y_n(x) = J_n(x) \left( A + B \int \frac{\ensuremath{\mathrm{d}}x}{x J_n(x)} \right) . $

Otra manera de escribir la segunda solución es la función de Weber o de Newman

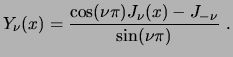
$\displaystyle Y_\nu(x) = \frac{ \cos(\nu\pi) J_\nu(x) - J_{-\nu} }{ \sin(\nu\pi) } . $

De esta manera, $ \forall \nu$ la solución general se puede escribir como

$\displaystyle y(x)= A J_n(x) + B Y_n(x) . $

La función generatriz asociada a las funciones de Bessel es $ G(x,t) = e^{\frac{1}{2}x \left( t - \frac{1}{t} \right)}$ , por tanto, podemos desarrollar $ G(x,t)$ como una serie de potencias de $ t$ cuyos coeficientes son las funciones de Bessel, esto es

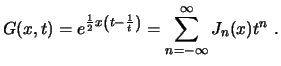
$\displaystyle G(x,t) = e^{\frac{1}{2}x \left( t - \frac{1}{t} \right)} = \sum_{n=-\infty}^{\infty} J_n(x) t^n . $

Derivando $ G(x,t)$ respecto de $ x$ podemos obtener la siguiente relación de recurrencia para las derivadas de las funciones de Bessel

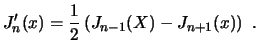
$\displaystyle J_n'(x) = \frac{1}{2} \left( J_{n-1}(X) - J_{n+1}(x)\right) . $

Derivando $ G(x,t)$ respecto $ t$ podemos obtener otra relación de recurrencia

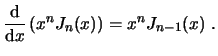
$\displaystyle \frac{\ensuremath{\mathrm{d}}}{\ensuremath{\mathrm{d}}x} \left( x^n J_n(x) \right) = x^n J_{n-1}(x) . $

Otra manera de representar las funciones de Bessel es la integral

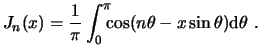
$\displaystyle J_n(x) = \frac{1}{\pi} \int^\pi_0\!\!\!\cos( n\theta - x \sin\theta)\ensuremath{\mathrm{d}}\theta . $

Si se modifica la ecuación de Bessel de la forma siguiente $ x^2 y''(x) + x y'(x) - (x^2 + \nu^2)y(x) = 0$ , la solución general se escribe como $ y(x)= A J_\nu(i x) + B Y_\nu(i x)$ . A partir de esto, se definen las funciones modificadas de Bessel:

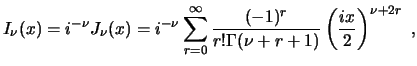
$\displaystyle I_\nu(x) = i^{-\nu} J_\nu(x) = i^{-\nu} \sum_{r=0}^\infty \frac{(-1)^r}{r! \Gamma(\nu+r+1)} \left( \frac{ix}{2} \right)^{\nu+2r} , $

$\displaystyle K_\nu(x) = \frac{\pi}{2} i^{\nu+1} \left[ i Y_\nu(i x) + J_\nu( i x ) \right] . $

En estas condiciones, la solución general se puede expresar

$\displaystyle y(x) = A I_\nu(x) + B K_\nu(x) . $

Las funciones propias de la ecuación de Bessel, imponiendo que $ y(0)$ sea acotada, los valores propios de la ecuación cumplen $ J_0(\sqrt{\lambda}) = 0$ con $ \lambda \neq 0$ . Sean los $ z_n$ los ceros de la función de Bessel de orden cero, los valores propios vienen dados por $ \lambda_n = \left( \frac{z_n}{L} \right)^2$ y las funciones propias son:

$\displaystyle \phi_n(x) = J_0\left( z_n \frac{x}{L}\right) . $

Su norma, con $ w(x) = x$ , es

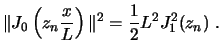
$\displaystyle \Vert J_0\left( z_n \frac{x}{L}\right)\Vert^2 = \frac{1}{2} L^2 J_1^2(z_n) . $

3.3 Polinomios de Legendre

La ecuación diferencial de Legendre es

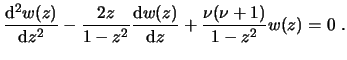
$\displaystyle \frac{\ensuremath{\mathrm{d}}^2 w(z)}{\ensuremath{\mathrm{d}}z^2}... ...hrm{d}}w(z)}{\ensuremath{\mathrm{d}}z} + \frac{\nu(\nu+1)}{1-z^2} w(z) = 0 . $

La solución general se escribe como $ w(z) = A P_\nu(x) + B Q_\nu(x)$ , donde $ P_\nu(x)$ es regular en $ \vert z\vert \leq 1$ sólo si $ \nu \in \mathbb{N}$ y $ Q_\nu(x)$ siempre es singular en $ z = \pm 1$ . Los polinomios de Legendre de orden $ l$ viene dado por

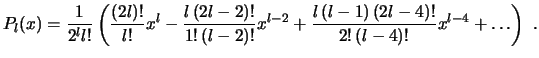
$\displaystyle P_l(x) = \frac{1}{2^l l!} \left( \frac{(2l)!}{l!} x^l - \frac{l ... ...!} x^{l-2} + \frac{l (l-1) (2l-4)!}{2! (l-4)!} x^{l-4} + \ldots \right) . $

La formula de Rodrigues permite calcular los polinomios de Legendre a partir de

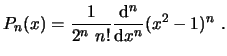
$\displaystyle P_{n}(x) = \frac{1}{2^n n!} \frac{\ensuremath{\mathrm{d}}^n}{\ensuremath{\mathrm{d}}x^n} (x^2-1)^n . $

La función generatriz de los polinomios de Legendre es

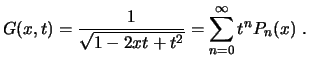
$\displaystyle G(x,t) = \frac{1}{\sqrt{1-2xt+t^2}} = \sum_{n=0}^\infty t^n P_n(x) . $

Imponiendo que $ y(\pm1)$ estén ambos acotadas, los Polinomios de Legendre son un conjunto completo, por lo que cualquier función se puede escribir como

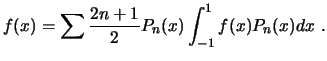
$\displaystyle f(x) = \sum \frac{2n+1}{2} P_n(x) \int_{-1}^1 f(x) P_n(x) dx . $

Las funciones asociadas de Legendre son la solución de la ecuación

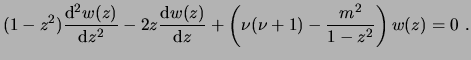
$\displaystyle (1-z^2) \frac{\ensuremath{\mathrm{d}}^2w(z)}{\ensuremath{\mathrm{... ...emath{\mathrm{d}}z} + \left( \nu(\nu+1) - \frac{m^2}{1-z^2} \right) w(z)=0 . $

La solución general se puede expresar como $ y(z) = A P_n^m(z) + B Q_n^m(z)$ , donde

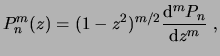
$\displaystyle P _n^m(z) = (1-z^2)^{m/2} \frac{\ensuremath{\mathrm{d}}^m P_n}{\ensuremath{\mathrm{d}}z^m} , $

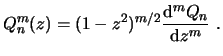
$\displaystyle Q _n^m(z) = (1-z^2)^{m/2} \frac{\ensuremath{\mathrm{d}}^m Q_n}{\ensuremath{\mathrm{d}}z^m} . $

3.4 Armónicos esféricos

Los armónicos esféricos son las soluciones de la parte angular de ecuación de Laplace en coordenadas esféricas, $ \Delta u(r,\theta,\varphi) = 0$ . Teniendo en cuenta la normalización a la unidad, los armónicos esféricos se pueden escribir como:

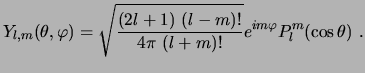
$\displaystyle Y_{l,m}(\theta, \varphi) = \sqrt{ \frac{(2l+1) (l-m)!}{4\pi (l+m)!}} e^{i m \varphi} P_l^m(\cos\theta) . $

La solución general de la ecuación de Laplace puede escribirse de la forma siguiente:

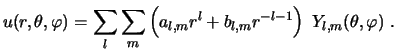
$\displaystyle u(r,\theta,\varphi) = \sum_l\sum_m \left( a_{l,m} r^l + b_{l,m} r^{-l-1} \right) Y_{l,m}(\theta,\varphi) . $

3.5 Otras funciones especiales

Los polinomios de Laguerre vienen dados por

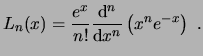
$\displaystyle L_n(x) = \frac{e^x}{n!} \frac{\ensuremath{\mathrm{d}}^n}{\ensuremath{\mathrm{d}}x^n} \left( x^n e^{-x} \right) . $

Los polinomios de Hermiten se pueden obtener a partir de

$\displaystyle H_n(x) = (-1)^n e^{x^2} \frac{\ensuremath{\mathrm{d}}^n e^{-x^2}}{\ensuremath{\mathrm{d}}x^n} . $